六年级数学教案《 圆柱的体积》

六年级数学教案《 圆柱的体积》

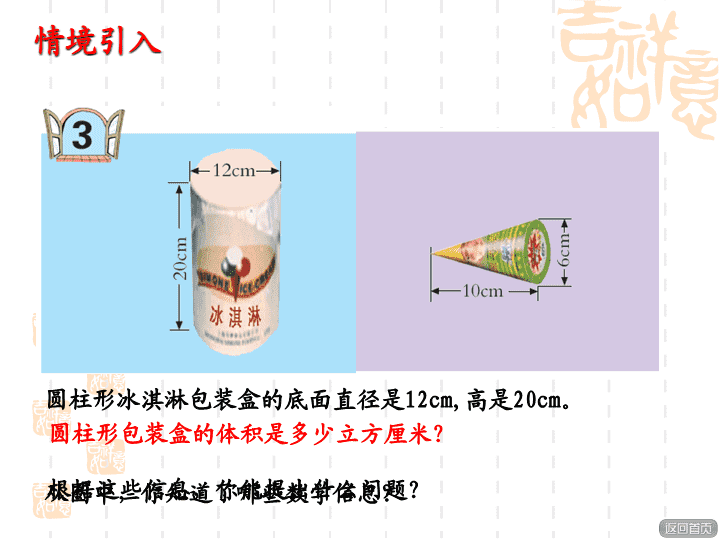
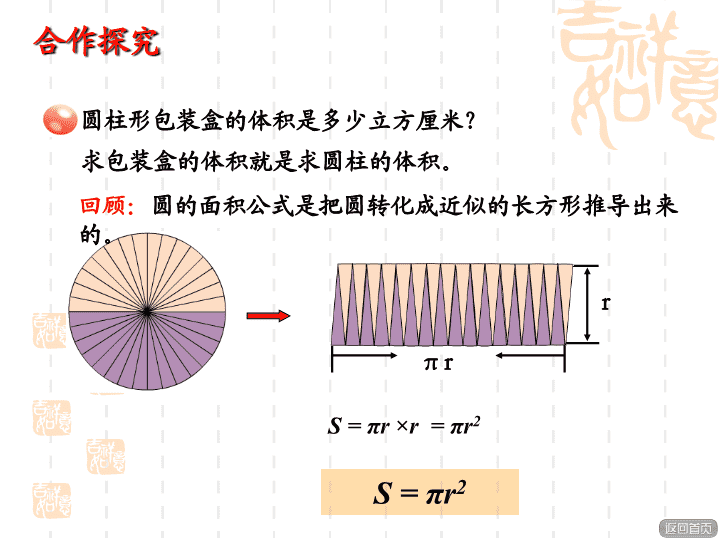
数学六年级下册 圆柱的体积 根据这些信息，你能提出什么问题？从图中，你知道了哪些数学信息？ 圆柱形冰淇淋包装盒的底面直径是12cm,高是20cm。 圆柱形包装盒的体积是多少立方厘米？ πr S = πr ×r = πr2 S = πr2 r 圆柱形包装盒的体积是多少立方厘米？ 求包装盒的体积就是求圆柱的体积。 回顾：圆的面积公式是把圆转化成近似的长方形推导出来 的。 ？ 猜想：通过刚才的回顾，你们能想办法将圆柱转化成 我们已经学过的立体图形吗？ 圆柱形包装盒的体积是多少立方厘米？ 友情提示： ①利用小组中的圆柱学具，把它转化成长方体？ ②观察对比，拼成的近似长方体的体积与原来的圆 柱体积有什么关系? ③拼成的近似长方体的底面积与原来圆柱的底面积 有何关系? ④ 拼成的近似长方体的高与原来的圆柱的高有什 么关系? ⑤根据长方体体积计算公式，推导出圆柱体体积公 式？ 圆柱等分的份数越多，拼成的图形越接近长方体。 …… V = S h 圆柱形包装盒的体积是多少立方厘米？ 底面积 高圆柱的体积 = × 长方体的体积=底面积 × 高 底面积： 3.14×（12÷2）2 = 3.14×36 = 113.04（平方分米） 体积：113.04×20 = 2260.8（立方分米） 答：这个圆柱形包装盒的体积是 2260.8 立方分米。 圆柱形包装盒的体积是多少立方厘米？ § 通过今天的学习，你有哪些收获？ 1.求下列图形的体积。（单位：厘米） 3.14×（8÷2）2×8 = 401.92（cm³） 拓展应用 3.14×（4÷2）2×10 = 125.6（cm³） 温馨提示： （1）最大的圆锥形 零件和圆柱体有 什么关系？ （2）削去的体积与 圆柱、圆锥体积 的关系。 （3）怎样求削去的 体积。有没有其 它方法? 2.哪根木料的体积大？ 3.14×（0.6÷2）2×8 = 3.14×0.09×8 = 2.2608（m3） 3.14×（0.4÷2）2×10 = 3.14×0.04×10 = 1.256（m3） 1.256<2.2608 答：第二根木料的体积大。 温馨提示： 请你想一想：要想知道哪一根 木料的体积大，必须知道什 么条件？ 拓展应用 3.有一个圆柱形油桶，从里面量底面直径是40厘米，高是50厘米。 （1）它的容积是多少升？ （2）若1升柴油重0.85千克，则这个油桶可装多少千克柴油？ （1）3.14×（40÷2）2×50 = 3.14×400×50 = 62800（cm3） = 62.8 （L） 答：它的容积是62.8升。 （2）0.85×62.8=53.38（千克） 答：这个油桶可装53.38千克柴油。 温馨提示： （1）在这里容积是什么意思 （2）第2问有什么需要注意的地方 拓展应用 4.从某地运来一车圆木，共50根，每根 圆木的直径0.4米，长是6米，这车圆木的体 积大约是多少？ 温馨提示： 此题是圆柱体积 在生活中的实 际应用。 要求这车圆木的 体积实际是求 什么？必须先 求什么？ 3.14×（0.4÷2）²×6×50 答：这车圆木的体积大约是37.68立方米。 =3.14×0.04×6×50 =3.14×0.04×300 =3.14×12 =37.68（立方米） 拓展应用 回顾本节课，通过本节课学习，你有什么 收获？