4-5反比例

4-5反比例

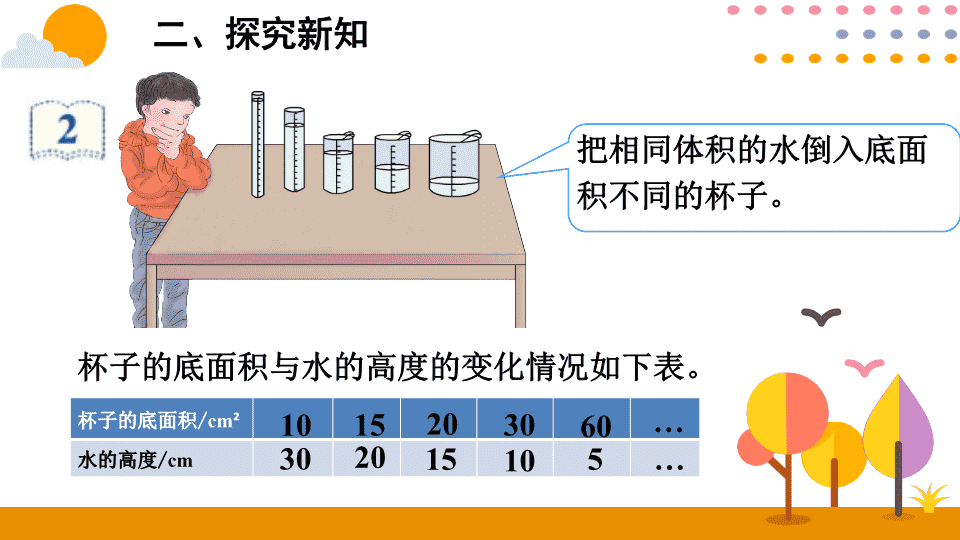
人民教育出版社六年级下册 比 例 第 5 课 时 反比 例 一、新课导入 成正比例的量有什么特征？ （ 3 ）两种量中相对应的两个数的比值一定。 （ 1 ）两种相关联的量。 （ 2 ）一种量变化 , 另一种量也随着变化。 二、探究新知 杯子的底面积与水的高度的变化情况如下表。 杯子的底面积 / cm ² 水的高度 / cm 10 30 15 20 20 15 30 10 60 5 … … 把相同体积的水倒入底面积不同的杯子。 观察上表，回答下面的问题。 （1）表中有哪两种量？ （2）水的高度是怎样随着杯子底面积的大小变化而变化的？ （3）相对应的杯子的底面积与水的高度的乘积分别是多少？ 杯子的底面积 / cm ² 水的高度 / cm 10 30 15 20 20 15 30 10 60 5 … … 从上表可以看出，水的高度和杯子的底面积是 两种相关联的量 ，水的高度是随着杯子的底面积的变大而不断变小的，而且水的高度与杯子的底面积的 乘积总是一定 的。例如： 积 300 ，实际就是倒入杯子的水的体积。 用式子表示它们的关系就是： 底面积 × 高度 = 体 积（一定） 30×10=20 × 15=15 × 20= … =300 像这样，两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的 乘积 一定，这两种量就叫做成反比例的量，它们的关系叫做 反比例关系 。 在上面的实验中，高度和底面积是成反比例的量，高度与底面积成反比例关系。 如果用字母 x 和 y 表示两种相关联的量，用 k 表示它们的积（一定），反比例关系可以用下面的式子表示： x y ＝ k 如果长方形的面积一定，长与宽成反比例关系。 如果总价一定，单价与数量成反比例关系。 你能举出生活中反比例关系的例子吗？ 讨论交流： 如 何判断两个量是否成反比例关系？请举例说明。 判断两个量是否成反比例关系的基本步骤： 1. 首先判断两个量是否是相关联的量。 2. 然后再看两个量的积是否为定值。 三、巩固练习 每天运的吨数/ t 运货的天数/天 300 1 150 2 100 3 75 4 60 5 50 6 （1）表中有哪两种量？它们是不是相关联的量？ 表中有每天运的吨数和运货的天数两种量，它们是相关联的量。 三、巩固练习 （2）写出几组这两种量中相对应的两个数的积，并比较积的大小，说一说这个积表示什么。 300×1 ＝ 300 150×2 ＝ 300 100×3 ＝ 300 75×4 ＝ 300 60×5 ＝ 300 50×6 ＝ 300 积一定，这 个积表示这批货的总量。 三、巩固练习 （3）运货的天数与每天运的吨数成反比例关系吗？为什么？ 成反比例关系。因为每天运的吨数和运货的天数是两种相关联的量，而且它们的乘积一定，所以这两种量成反比例关系。 三、巩固练习 2 ．有 x 、 y 、 z 三个相关联的量，并有 xy = z 。 (1) 当 z 一定是， x 与 y 成 比例关系。 (2) 当 x 一定是， z 与 y 成 比例关系。 (3) 当 y 一定是， z 与 x 成 比例关系。 反 正 正 四、课堂小结 反比例的意义： 两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量中相对应的两个数的 乘积 一定，这两种量就叫做 成反比例的量 ，它们的关系叫做 反比例关系 。反比例关系可以用“ xy = k （一定）”来表示。