六年级下册数学课件《8、图形的运动》(2) 苏教版(共21张PPT)

六年级下册数学课件《8、图形的运动》(2) 苏教版(共21张PPT)

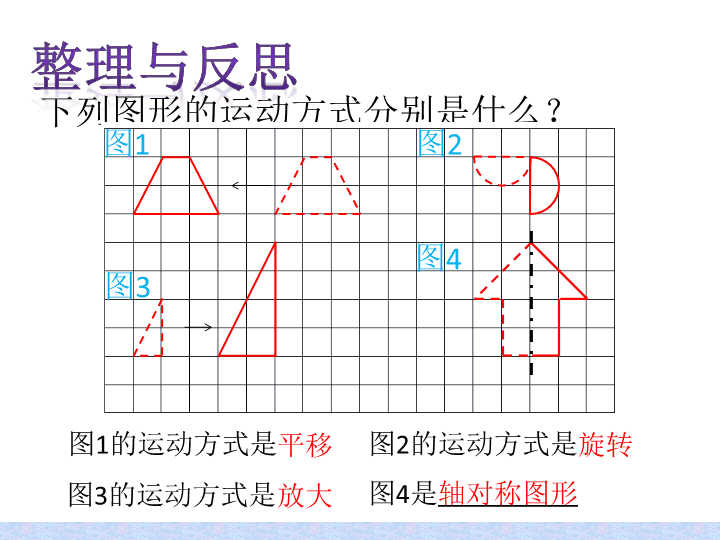
图形的运动 小学数学苏教 2011 课标版六年级下册 下列图形的运动方式分别是什么？ 图 1 图 2 图 3 图 4 图 1 的运动方式是 图 2 的运动方式是 图 3 的运动方式是 图 4 是 轴对称图形 整理与反思 平移 旋转 放大 什么样的图形是轴对称图形呢？ 轴对称图形 对折 轴对称图形 对折 轴对称图形 对折 轴对称图形 完全重合 对折 对称轴 轴对称图形 轴对称图形 下面哪些图形是轴对称图形？ （ ）是轴对称图形。 长方形 正方形 等腰三角形 等腰梯形 圆 等边三角形 半圆 对称轴条数 图形名称 1 条 2 条 3 条 4 条 无数条 轴对称图形 你能说说下面的图形各有几条对称轴吗？ 长方形 正方形 等腰三角形 等腰梯形 圆 等边三角形 半圆 先找关键点，再描对应点，最后连线。 轴对称图形 你会画出房子图的另一半，使它成为轴对称图形么？ 关键点 对应点 梯形向（ ）平移了（ ）格。 左 平移 关键点 对应点 下面的梯形是怎样平移的？ 5 图 1 半圆绕着（ ）点（ ）时针旋转了（ ） 。 。 B 旋转 下面的半圆是怎样旋转的？ 逆 A B 图 2 90 三角形是按（ ： ）的比（ ）。 2 1 放大和缩小 下面的图形是怎么变化的？ 放大 图 3 观察这三幅图，分别说说运动后的图形和原来相比什么变了，什么没变？ 图 1 图 2 图 3 平移和旋转 只改变图形的位置 ， 不改变形状和大小 。 放大和缩小 只改变图形的大小 ， 不改变图形的形状 。 小组讨论 练习与实践 1. 将 展开来得到的图形是（ ）。 A B C D 2. 对图形进行平移、旋转、放大或缩小时，图形的（ ）不变。 A 大小 B 位置 D 形状 C 面积 C D 3. 把右图绕点 O 顺时针旋转 90 。 ，得到的图形是（ ）。 O A B C D A 4. （ 1 ）画出图形 A 的另一半，使它成为一个轴对称图形。 （ 2 ）把图 B 向右平移 5 格，再向上平移 3 格。 练习与实践 （ 3 ）把图 C 绕点 O 逆时针旋转 90 。 。 （ 4 ）把图 D 按 1:2 的比缩小。 A B C O D 回忆一下，我们在推导三角形的面积公式时，用过哪两种图形的运动方式？ 转化与应用 ┑ ┑ a h 三角形 S=ah÷2 旋转 ----- 平移 ----- 拼 4 ×4 ＝ 16 （ cm 2 ） 5. 你能用图形运动的知识来求出阴影部分的面积么？（单位：厘米） 转化与应用 4 （ 1 ） （ 2 ） O （ 3 ） 2 45 。 45 。 4 π × 2 2 ÷ 2 ＝ 2 π （ cm 2 ） 圆面积： π × 4 2 ÷ 4 ＝ 4 π （ cm 2 ） 三角形面积： 4× 4 ÷ 2 ＝ 8 （ cm 2 ） 阴影面积： 4 ×3.14 —8=4.56 （ cm 2 ） 4 1 原来阴影面积： 4.56 ÷ 2 =2.28 （ cm 2 ） 欣赏与创作 你知道这些图案分别用什么方法设计出来的吗？ 轴对称 旋转 放大 平移 这节课你有什么收获？