小学数学精讲教案5_5_2 带余除法（二） 学生版

小学数学精讲教案5_5_2 带余除法（二） 学生版

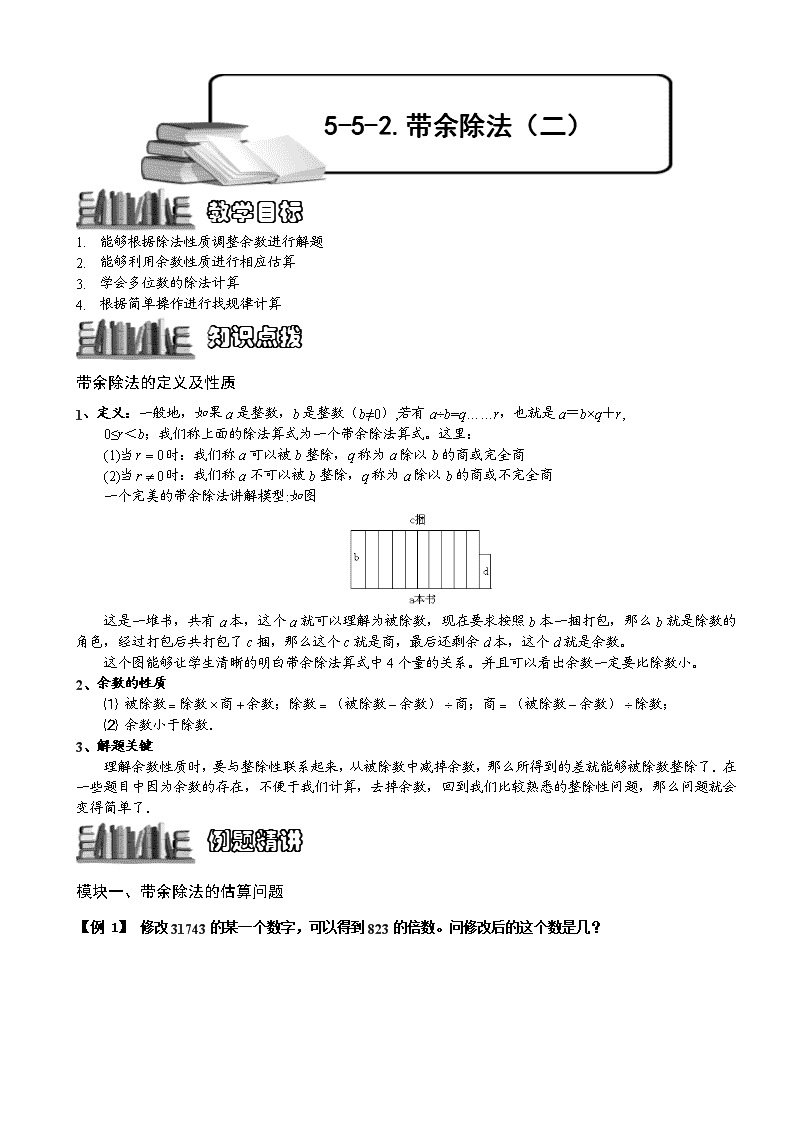
‎5-5-2‎‎.带余除法（二）‎ 教学目标 1. 能够根据除法性质调整余数进行解题 2. 能够利用余数性质进行相应估算 3. 学会多位数的除法计算 4. 根据简单操作进行找规律计算 知识点拨 带余除法的定义及性质 ‎1、定义：一般地，如果a是整数，b是整数（b≠0）,若有a÷b=q……r，也就是a＝b×q＋r, ‎ ‎0≤r＜b；我们称上面的除法算式为一个带余除法算式。这里：‎ ‎(1)当时：我们称a可以被b整除，q称为a除以b的商或完全商 ‎(2)当时：我们称a不可以被b整除，q称为a除以b的商或不完全商 一个完美的带余除法讲解模型:如图 这是一堆书，共有a本，这个a就可以理解为被除数，现在要求按照b本一捆打包，那么b就是除数的角色，经过打包后共打包了c捆，那么这个c就是商，最后还剩余d本，这个d就是余数。‎ 这个图能够让学生清晰的明白带余除法算式中4个量的关系。并且可以看出余数一定要比除数小。‎ ‎2、余数的性质 ‎⑴ 被除数除数商余数；除数（被除数余数）商；商（被除数余数）除数；‎ ‎⑵ 余数小于除数．‎ ‎3、解题关键 理解余数性质时，要与整除性联系起来，从被除数中减掉余数，那么所得到的差就能够被除数整除了．在一些题目中因为余数的存在，不便于我们计算，去掉余数，回到我们比较熟悉的整除性问题，那么问题就会变得简单了．‎ 例题精讲 模块一、带余除法的估算问题 【例 1】 修改31743的某一个数字，可以得到823的倍数。问修改后的这个数是几？ ‎ 【例 1】 有48本书分给两组小朋友，已知第二组比第一组多5人．如果把书全部分给第一组，那么每人4本，有剩余；每人5本，书不够．如果把书全分给第二组，那么每人3本，有剩余；每人4本，书不够．问：第二组有多少人? ‎ 【例 2】 一个两位数除以13的商是6，除以11所得的余数是6，求这个两位数．‎ 【例 3】 在小于1000的自然数中，分别除以18及33所得余数相同的数有多少个?(余数可以为0) ‎ 【例 4】 托玛想了一个正整数，并且求出了它分别除以3、6和9的余数．现知这三余数的和是15．试求该数除以18的余数．‎ 模块二、多位数的余数问题 【例 5】 除以13所得余数是_____.‎ 【巩固】 的余数是多少？‎ 【例 1】 除以41的余数是多少？‎ 【例 2】 已知，问：除以13所得的余数是多少？‎ 模块三、找规律计算 【例 3】 科学家进行一项实验，每隔5小时做一次记录。做第十二次记录时，挂钟的时针恰好指向9，问做第一次记录时，时针指向几?‎ 【例 4】 一筐苹果分成小盒包装，每盒装只，剩只；每盒装只，剩只。每盒装只，剩 只。‎ 【例 5】 著名的斐波那契数列是这样的：1、1、2、3、5、8、13、21……这串数列当中第2008个数除以3所得的余数为多少？‎ 【巩固】 有一列数：1，3，9，25，69，189，517，…其中第一个数是1，第二个数是3，从第三个数起，每个数恰好是前面两个数之和的2倍再加上1，那么这列数中的第2008个数除以6，得到的余数是 ．‎ 【巩固】 有一列数排成一行，其中第一个数是3，第二个数是10，从第三个数开始，每个数恰好是前两个数的和，那么第1997个数被3除所得的余数是多少？‎ 【例 1】 有一串数：1，1，2，3，5，8，……，从第三个数起，每个数都是前两个数之和，在这串数的前2009个数中，有几个是5的倍数？‎ 【例 2】 将七位数“1357924”重复写287次组成一个2009位数“13579241357924…”。删去这个数中所有位于奇数位上的数字；按上述方法一直删除下去直到剩下一个数字为止，则最后剩下的数字是 ‎ 【例 3】 ‎30粒珠子依8粒红色、2粒黑色、8粒红色、2粒黑色…的次序串成一圈，一只蚂蚱从第2粒黑珠子起跳，每次跳过6粒珠子落在下一粒珠子上，这只蚂蚱至少要跳 次才能落到黑珠子上。‎ 【例 4】 有这样一类2009位数，它们不含有数字0，任何相邻两位（按照原来的顺序）组成的两位数都有一个约数和20相差1，这样的2009位数共有________个．‎ 【例 1】 在两位数10，11，…，98，99中，将每个被7除余2的数的个位与十位之间添加一个小数点，其余的数不变．问：经过这样改变之后，所有数的和是多少?‎ 模块四、特殊的数字9‎ 【例 2】 将从1开始的到103的连续奇数依次写成一个多位数：A＝13579111315171921……9799101103。则数a共有_____位，数a除以9的余数是___。‎