六年级下册数学试题-奥数：一题多解

六年级下册数学试题-奥数：一题多解

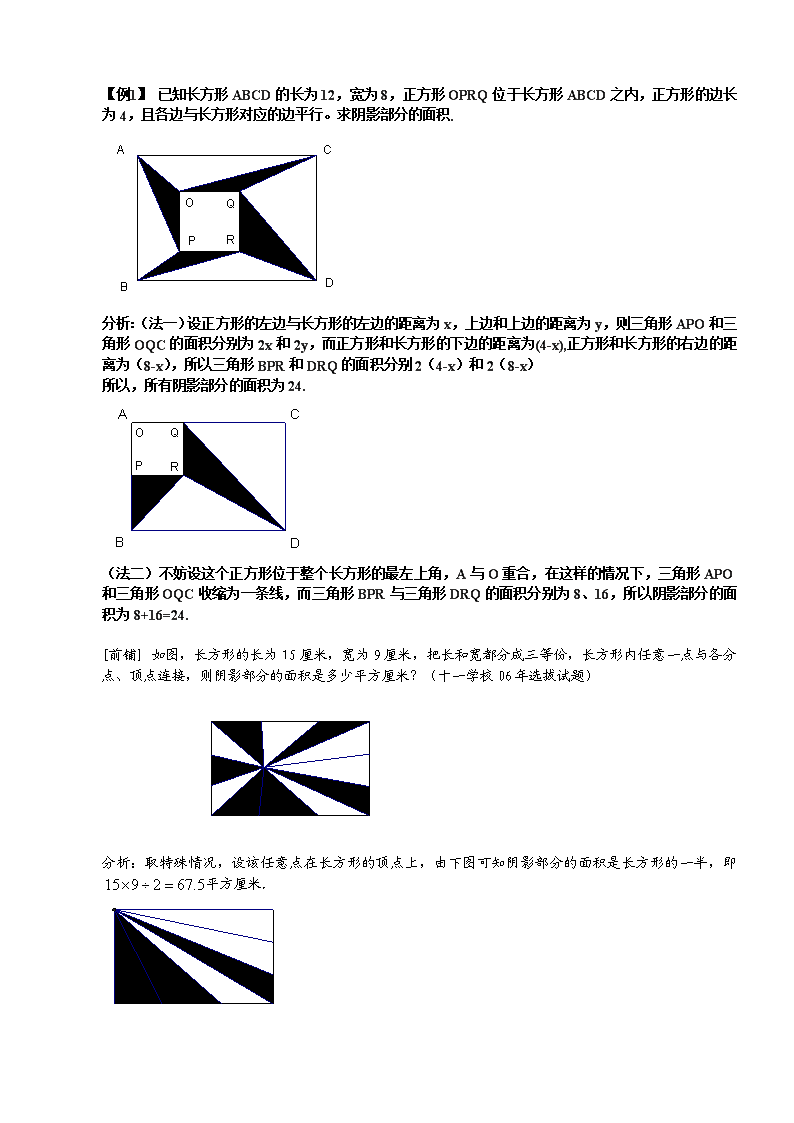
第七讲一题多解教学目标学奥数的本意是开发智力，整合知识。我们通过一题多解的训练形式，要努力形成举一反三、融会贯通的能力，常见的解题方法主要是算术方法和方程等，算术方法是我们解小学奥数题的主力，方程作为一种数学工具也是我们解题时经常依赖的，除了这些以外，我们还有很多非常规、非典型的解题方法，如（1）特殊值法；（2）利用图形解题；（3）取特殊情形、极限考虑。一个正三角形中内接一个圆，圆中又内接一个小三角形，问小三角形的面积是大三角形面积的几分之几？想挑战吗　？分析：转动小三角形使小三角形和大三角形相反方向，容易看出小三角形的面积是大三角形的四分之一.专题精讲Ⅰ考虑特殊情况与特殊值特殊情况与特殊值的方法一般只适合用于巧解填空题，利用特殊情况和特殊值的原则，主要有：(1）不违背题目条件；(2）特殊情况或特殊值代入原题后不会产生逻辑或数值上的矛盾；(3）特殊情况或特殊值有利于题目的解决.由于特殊情况和特殊值的特殊性，建议大家不要在解答题或证明题中使用这种方法，这种方法仅仅作为一种应试技巧和参考. 【例1】已知长方形ABCD的长为12，宽为8，正方形OPRQ位于长方形ABCD之内，正方形的边长为4，且各边与长方形对应的边平行。求阴影部分的面积.分析：（法一）设正方形的左边与长方形的左边的距离为x，上边和上边的距离为y，则三角形APO和三角形OQC的面积分别为2x和2y，而正方形和长方形的下边的距离为(4-x),正方形和长方形的右边的距离为（8-x），所以三角形BPR和DRQ的面积分别2（4-x）和2（8-x）所以，所有阴影部分的面积为24.（法二）不妨设这个正方形位于整个长方形的最左上角，A与O重合，在这样的情况下，三角形APO和三角形OQC收缩为一条线，而三角形BPR与三角形DRQ的面积分别为8、16，所以阴影部分的面积为8+16=24.[前铺]如图，长方形的长为15厘米，宽为9厘米，把长和宽都分成三等份，长方形内任意一点与各分点、顶点连接，则阴影部分的面积是多少平方厘米？（十一学校06年选拔试题）分析：取特殊情况，设该任意点在长方形的顶点上，由下图可知阴影部分的面积是长方形的一半，即平方厘米. 【例1】如图，有三个正方形ABCD、BEFG和CHIJ，其中正方形ABCD的边长是10，正方形BEFG的边长是6，那么三角形DFI的面积是．分析：（法一）S△DIF＝SABCD+SCHIJ+S△DIJ－SBEFG－SADFG－SADFG－SEHIF＝100+a2+a(10－a)－36－(10－6)(10+6)－(6+a)(4+a)＝20。（法二）还可以利用三角形DFI面积=DFC的面积（法三）极限考虑，令正方形JCHI边长为0，这样I就变成C点，所以三角形DFI面积=DFC的面积.或者考虑正方形JHIJ与正方形ABCD等大的情形，在这种情形下，三角形DFI面积=10×（10-6）=20.[前铺]（★★★奥林匹克数学竞赛）如下图，ABCD、CEFG均为正方形，已知ABCD的边长是12，试求三角形BFD的面积。分析:（法一）设小正方形CEFG的边长为，则（法二）直线BD与CF平行，所以三角形BFD与三角形BCD面积相等，则.[点评]利用五大模型中的梯形两腰上的三角形相等.（法三）取极限情况，令小正方形CEFG的边长为零（如下左图），则点F经线段FC滑至点C，所求三角形即为BCF；令小正方形CEFG的边长与大正方形的边长相等（如下右图），则三角形BFD的面积即为大正方形的一半。 [点评]可以先让学生随便先设一些数据来算，再用方法一，再讲方法三，这样最能体现一个老师讲这道题的能力。【例1】五年级二班数学考试的平均分数是85分，其中的人得80分以上（含80分），他们的平均分数是90分。求低于80分的人的平均分。分析：（法一）设该班级有名同学，低于80分的人的平均分为，则得方程（法二）不妨设该班只有3名同学，其中2人得80分以上，他们恰好都是90分，各比平均分多5分，则另一名同学应比平均分少分，即分。【例2】甲班与乙班学生同时从学校出发去公园，两班步行的速度均为每小时5千米。学校有一辆汽车，空车行驶的速度是每小时60千米，这辆汽车恰好能坐一个班的学生，搭载学生时的行驶速度是每小时50千米。为了使两班学生在最短时间内到达公园，甲班学生步行了全程的几分之几？分析：（法一）运用比例结合图形解.设甲班先步行，则甲班由C至B的时间与汽车由C经A至B的时间相等。假设汽车的速度一直都是50千米/时，则CA+AB=（）CB=10CB。但实际上汽车在BA段的速度变为60，则相应的等量关系应变为CB+AB+AB=10CB，整理得AB=CB；又CB=AD，所以CD=（）CB=CB，即甲班学生步行了全程的。 （法二）设全程为千米，甲班学生步行了千米，根据甲班上车前的步行时间与汽车的行驶时间相等，可得方程：(法三)运用特殊值的方法：设汽车行驶了1个单位的路程后返回去接乙班学生，掉头时乙班学生们已走了个单位的路程，因此汽车和乙班学生相遇时，学生分别又走了，汽车走了，这时候汽车距离甲班学生个单位路程，汽车要追上甲班学生还需要行驶个单位路程.因此总路程为，其中甲班学生走了个单位的路程.因此甲班学生走的路程是全程的.Ⅱ从不同角度思考问题【例1】图是由正方形和半圆形组成的图形。其中P点为半圆周的中点，Q点为正方形一边的中点。已知正方形的边长为10，那么阴影部分面积是多少？（π取3.14.）分析：（法一）阴影面积的“加减法”。因为阴影部分面积不是正规图形，所以通过整个面积减去空白部分面积来求解。过P点向AB作垂线，这样空白部分面积分成上面的三角形和下面的梯形，这样阴影面积=整个面积-空白面积=（正方形ABCD+半圆）—（三角形+梯形）=（10×10+π×5×5÷2）-[15×5÷2+（5+15）×5÷2]=51.75[总结]这种方法是小升初中最常用的方法，一定要学会这种处理思路。 （法二）面积的“加减法”和“切割法”综合运用，思路出现正方形，出现弧线时，注意两个考点：1.半叶形2。1/4圆，所以我们可以先把面积补上再减去补上的面积S1=正方形-1/4圆=5×5-1/4×π×5×5上面阴影面积=三角形APE-S1=15×5÷2-5×5-1/4×π×5×5下面阴影面积=三角形QPF-S2=10×5÷2-（5×5-1/4×π×5×5）所以阴影面积=（15×5÷2-5×5+1/4×π×5×5）+（10×5÷2-5×5+1/4×π×5×5）=51.75（法三）面积的“切割法”出现正方形，出现弧线时，注意两个考点：1.半叶形2.1/4圆，这样可以考虑把阴影面积切成几个我们会算的规则图形半叶形S1=正方形-1/4圆=5×5-1/4×π×5×5上面阴影面积=三角形ADP+S1=10×5÷2+5×5—1/4×π×5×5下面阴影面积=三角形QPC+S2=5×5÷2+5×5—1/4×π×5×5阴影面积=（10×5÷2+5×5—1/4×π×5×5）+（5×5÷2+5×5—1/4×π×5×5）=51.75【例1】（★★★）如图，ABCG是4×7的长方形，DEFG是2×10的长方形，那么，三角形BCM的面积与三角形DCM的面积之差是多少？分析：（法一）公共部分的运用，这是小升初的常用方法，熟练找出公共部分是解题的关键。 GC=7，GD=10推出HE=3；BC=4，DE=2阴影BCM面积-阴影MDE面积=(BCM面积+空白面积)-(MDE面积+空白面积)=三角形BHE面积-长方形CDEH面积=3×6÷2-3×2=3.[总结]对于公共部分要大胆的进行处理,这样可以把原来无关的面积联系起来,达到解题的目的.(法二)画阴影的两个三角形都是直角三角形，而BC和DE均为已知的，所以关键问题在于求CM和DM．这两条线段之和CD的长是易求的，所以只要知道它们的长度比就可以了，这恰好可以利用平行线BC与DE截成的比例线段求得．分析GC=7，GD=10知道CD=3；BC=4，DE=2知道BC:DE=CM:DM所以CM=2，MD=1.阴影面积差为:4×2÷2-1×2÷2=3(方法三)连接BD[拓展]如图,已知圆的直径为20,S1-S2=12,求BD的长度.分析：S1加上空白部分面积即为半圆面积，S2加上空白部分面积即为三角形的面积.所以S1-S2等于半圆面积减去三角形面积，半圆的面积为102兀÷2=157，所以三角形的面积为157-12=145，所以三角形的底边边长为145×2÷20=14.5厘米. 【例1】如图，半圆ACB的直径为AB,△ABC为等腰直角三角形，△BCD为边长为2等边三角形，那么途中阴影部分面积为。分析：法一：阴影部分分为三角形ACD+弓形AC，可分别求。过D点作DF垂直交AC于F点，见下左图。∠BCD=60°,所以∠ACD=30°，那么在直角三角形FCD中，直角边DF=DC的一半=1；又AC=BC=2，所以三角形ACD的面积是1。设圆的半径为，在等腰直角三角形ABC中，根据面积相等有，则，因此弓形AC的面积是，所以阴影部分面积是。法二：取BC边的中点E，连接DE和CO，见下右图。DE是正三角形CBD在CB边上的高，则DE与AC垂直，那么，又，则阴影部分面积等于+弓形AC，即四分之一圆，同法一求得，所以阴影部分面积为。【例2】汽车甲和乙分别以每小时100千米和120千米的速度从Ａ城开往B城。甲车比乙车早l小时离开Ａ城，但同时到达B城。求两城间的路程。（法一）因为甲车先走了100千米，乙车每小时能追上甲车(120—100)=20(千米)，追100千米要用(100÷20)=5(小时)，乙车5小时共走120×5=600(千米)就是A、B两城间的路程。列算式为　　120［100÷(120—100)]＝600(千米)（法二）由于甲、乙两车行的路程相同，根据甲、乙两车速度的比是(100：120)=5：6可以知道，甲、乙两车所用时间的比为6：5，从而求出乙车用的时间为（小时）.故A、B两城间的路程为120×5=600（千米）.列算式为（千米）.（法三）两车各走一千米所需的时间差：（小时），由于两车所用的时间差为1小时，所以两车各走=600千米. 【例1】一项工程，甲单独做20天完成，乙单独做30天完成。甲、乙合作了几天后，乙因事请假，甲继续做，从开工到完成任务共用了16天。乙请假多少天?分析：(法一)假设乙没有请假，则两人合作16天，应完成超过单位“1”的，则乙请假（天）.(法二)甲一共干了16天，完成了×16=，还有l-=，是乙做的，乙干了(天)，休息了16—6=10(天).(法三)设乙请假x天.，解得x=10.【例2】甲乙二人的年龄（均超过10岁）相差21岁，试问：有没有可能某一年，两人岁数的两位数字恰好相反？分析：（法一）如果存在，设二人的岁数分别为、，其中>，则年龄差为，应是9的倍数，而21不能被9整除。（法二）如果存在，设年纪小的那个人年龄为，那么如果b不等于9的话，年纪大的那个人的年龄为，因为a+b≠（a+2）+（b+1）所以这两个两位数不可能数字恰好相反（否则应该相等），如果b=9，那么年纪大的那个人的年龄应该是个整十数，即a=0，这显然不可能，所以没有可能某一年，两人的两位数字恰好相反.[拓展]一个两位数被它的各位数字之和除去，问余数最大是多少？分析：要使得余数最大，应首先使得这个两位数的两个数字之和尽可能大.（法一）设这个两位数为，即求除以的余数，又，所以只要求除以的余数。=9时，依次检验取9、8、……、0时的余数，分别为9、13、1、6、11、3、9、4、1、0；=8时，依次检验取9、8、……、0时的余数，分别为4、8、12、2、7、0、6、2、0；=7时，依次检验取时，余数为15，而此后一定不会超过7+8=15，则余数也不会超过15，所以15即为最大的余数. （法二）最大，余数才可能最大，按照的和从大到小检验：=18时，只能是99，余数是9；=17时，可能是98或89，相应的余数是13或4；=16时，可能是97、88或79，相应的余数是1、8或15；而当≤15时，余数应小于等于14，因此15即为最大的余数.【例1】12和60是很有趣的两个数，这两个数的积恰好是这两个数的和的10倍：12×60＝720,12＋60＝72。满足这个条件的正整数还有哪些？分析：（法一）设满足条件的正整数对是a和b（ab）。依题意有ab=10(a+b)ab=10a+10b,ab-10a=10ba(b-10)=10ba==10+因为a是正整数，所以b是大于10的整数，并且（b-10）是100的约数。推知b=11,12,14,15,20，相应地得到a=110,60,35,30,20。即所求的正整数对还有11,110；14,35；15,30；20,20；四对。（法二）变形为分数分拆由因为=所以可得到11,110；14,35；15,30；20,20；四对.[拓展]对于两个不同的整数，如果它们的积能被和整除，就称为一对“好数”例如70与30，那么在1，2，……，16这16个整数中，有好数多少对？分析：（法一）不妨设它们的积是和的k倍，设这两个数为,则有,化为,由于，最多只能取16，所以，k的值不超过16×16÷（16+16）=8，由于对称，所以不妨设a≥b，显然当b≤2k时，a≥b，所以有如下判断：显然k=1时，b-k只能取值1，此时2，当k=2时，b-k能取1、2，对应的3、4，6、4；当k=3时，b-k能取1、3，对应的4、6，12、6；当k=4时，b-k能取1、2、4，对应的5、6、8，20、12、8；当k=5时，b-k能取1、5，对应的6、10，30、10；当k=6时，b-k能取1、2、3、4、6，对应的7、8、9、10、12，42、24、18、15、12；当k=7时，b-k能取1、7，对应的8、14，56、14；当k=8时，b-k能取1、2、4、8，对应的9、10、12、16，72、40、24、16； 从中筛选出符合条件的a、b值有：（3、6）（4、12）（6、12）（10、15）四对.专题展望zhanwang1wzhanwang欲知更多方法，请关注寒假班！练习七1.下图是一个各条边长度分别为、、的直角三角形。将它的短直角边对折到斜边上去与斜边相重合，那么右图中的阴影部分的面积是多少？分析：（法一）在右图中三角形ACE和ACB面积相等；BC=EC=5cm，所以DB=cm，又三角形ACE、ACB、ABD的高AB（AE）相等，所以它们的面积之比是为5：5：8。三角形CDE的面积是，所以阴影部分的面积是。（法二）设AB（AE）长为cm，则有方程，解得，所以阴影部分面积是。2.在一个梯形内部有两个面积分别是6和8的三角形，梯形下底的长是上底的倍，试求阴影部分的面积。分析：14.提示：设上底为3，下底为4，则梯形的高是4+4=8，梯形面积是（3+4）=28，空白部分面积为28–6–8=14。3.如图，在一个梯形内有两个三角形的面积分别为10和12，已知梯形的上底是下底长的。那么余下的阴影部分的面积是多少？ 分析：（法一）设上底为，那么下底为，则上下两个三角形的高分别为，，梯形的高是，其面积为，阴影部分面积为。（法二）不妨设上底为2，则下底为3，则上下两个三角形的高分别为，，梯形的高是，其面积为，阴影部分的面积为。1.我们规定两人轮流做一个工程是指，第一个人先做一个小时，第二个人再做一个小时，然后再由第一个人做一个小时，然后又由第二个人做一个小时，如此反复，做完为止。如果甲、乙轮流做一个工程需要9.8小时，而乙、甲轮流做同样的工程只需要9.6小时，那乙单独做这个工程需要多少小时？分析：甲乙甲乙…甲1小时乙0.8小时；乙甲乙甲…乙1小时甲0.6小时；甲0.4小时乙0.2小时。即甲工作2小时，相当于乙1小时。所以，乙单独工作需9.8－5+5÷2＝7.3小时。2.乙两队开挖一条水渠。甲队单独挖要8天完成，乙队单独挖要12天完成，现在两队同时挖了几天后，乙队调走，余下的甲队在3天内挖完。乙队挖了多少天?分析：（法一）解：设甲、乙两队合挖了天。（法二）把水渠的全长看作单位“l”，从单位“l”中减去甲队3天挖的，剩下的就是甲、乙两队同时挖的。用剩下的工作量除以甲、乙两队的工作效率之和等于两队合挖用的天数，也就是乙队挖的天数。 成长故事谷仓里的金表让成功更有效率哲理的故事一个农场主在巡视谷仓时不慎将一只名贵的金表遗失在谷仓里。他遍寻不获，便在农场门口贴了一张告示，要人们帮忙，悬赏100美元。人们面对重赏诱惑，无不卖力地四处翻找，无奈谷仓内谷粒成山，还有成捆成捆的稻草，要想在其中找寻一块金表如同大海捞针。人们忙到太阳下山仍没找到金表，他们不是抱怨金表太小，就是抱怨谷仓太大、稻草太多，一个个放弃了100美元的诱惑。只有一个穷人家的小孩儿在众人离开之后仍不死心，努力寻找，他已整整一天没吃饭了，希望在天黑之前找到金表，解决一家人的吃饭困难。天越来越黑，小孩儿在谷仓内坚持寻找。突然他发现一切喧闹静下来后有一个奇特的声音，那声音“滴答，滴答”不停地响着。小孩儿顿时停止寻找。谷仓内更加安静，滴答声响得十分清晰。小孩循声找到了金表，最终得到了100美元。