六年级数学下册专题教程第七模块用转化策略解决问题新人教版

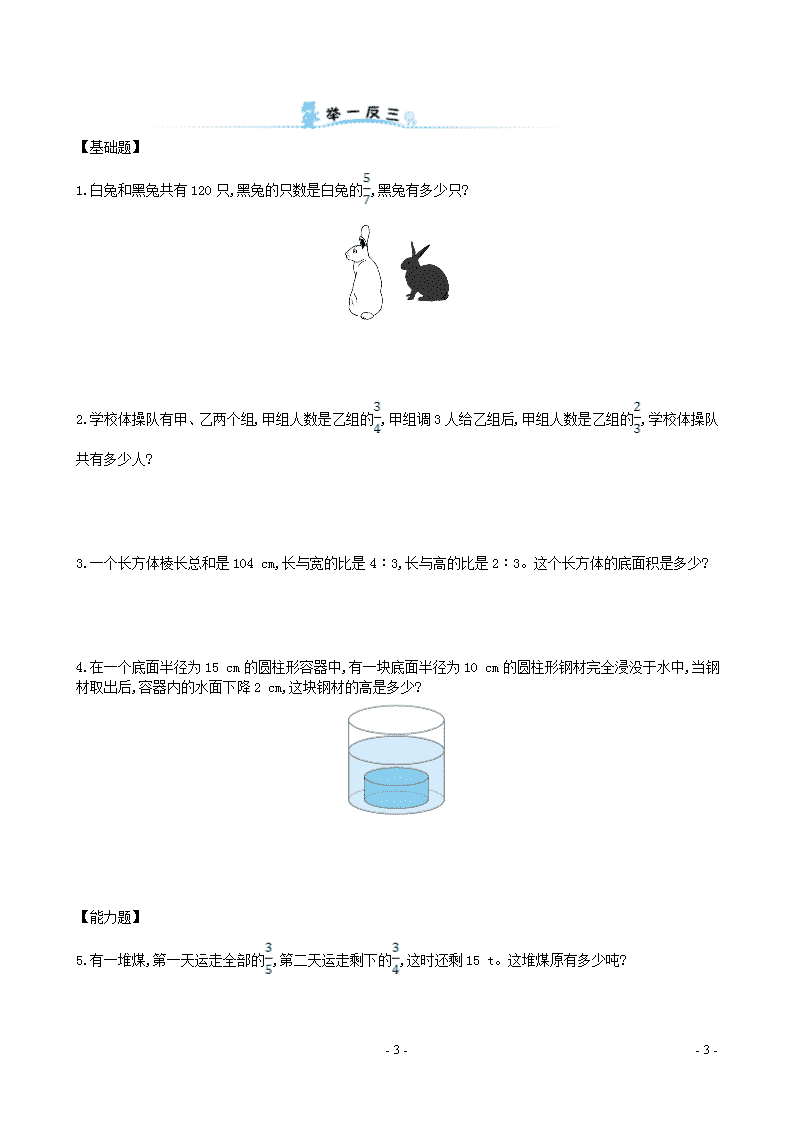
六年级数学下册专题教程第七模块用转化策略解决问题新人教版

第七模块　用转化策略解决问题 ‎【教法剖析】‎ ‎　　转化法:转化策略是解决问题时经常采用的方法,就是在解题过程中,不断转化解题方向,从不同的角度、不同的侧面去探讨问题的解法,寻找最佳的方法。它能把复杂的题目变简单,把生疏的题目变成简单的题目,从而化繁为简,化难为易,使问题迎刃而解。‎ 例1　向阳小学共有学生630人,其中女生人数是男生的,该校有女生多少人?‎ ‎【助教解读】‎ ‎ 根据女生人数是男生的,可以把男生看作5份,那么女生就是4份,总人数就是9份。根据总人数有630人,可算出一份是多少人,从而求出女生人数;也可以把女生人数是男生的转化为女生与男生的人数比是4︰5,又知道总人数是630人,这样就变成按比例分配的问题了。‎ ‎ 解法1:630÷(4+5)=70(人) 70×4=280(人)‎ ‎ 解法2:4+5=9 630×=280(人)‎ ‎　　答:该校有女生280人。‎ ‎【经验总结】‎ ‎ 把一个量是另一个量的几分之几转化成相对应的份数,或转化成两个量的 比,有时可使问题简化。‎ 例2　明德小学六(1)班人数是六(2)班的,如果从六(2)班调1人到六(1)班,六(1)班人数是六(2)班的。两个班原来共有多少人?‎ ‎【助教解读】‎ ‎ 原来六(1)班的人数是六(2)班的,可知六(1)班的人数占两个班总人数的,后来六(1)班的人数是六(2)班的,可知六(1)班的人数占两个班总人数的,前后两次六(1)班人数占总人数的分率的差就是六(1)班增加的1人占总人数的分率。‎ ‎ 1÷=1÷=99(人)‎ ‎ 答:两个班原来共有99人。‎ - 5 -‎ - 5 -‎ ‎【经验总结】‎ ‎ 本题中,两个班的人数都发生了变化,而总人数是不变的,所以应把总人数转化为单位“1”,找出题中已知量占单位“1”的对应分率即可求解。‎ 例3　一个长方体棱长总和是156 cm,长与宽的比是3︰2,宽与高的比是4︰3。这个长方体的体积是多少?‎ ‎【助教解读】‎ ‎ 长与宽的比是3︰2=6︰4,宽与高的比是4︰3,则长、宽、高的比是6︰4︰3,在长方体中长、宽、高各4条,用156除以4,得出一组长、宽、高的和,再按比例分配,求出长、宽、高,再求出体积。‎ ‎ 3︰2=6︰4　长︰宽︰高=6︰4︰3‎ ‎ 156÷4=39(cm)　39×=18(cm)　39×=12(cm)　39×=9(cm)‎ ‎ 18×12×9=1944(cm3)‎ ‎ 答:这个长方体的体积是1944 cm3。‎ ‎【经验总结】‎ ‎ 长与宽的比是3︰2,宽与高的比是4︰3,把宽看作中间数,根据比的基本性质,把宽对应的份数转化为相等的数,再得出长、宽、高的比。‎ 例4　如图所示,老师用纸板做了一个学具,你能计算出它的体积吗?‎ ‎【助教解读】‎ ‎ 这是一个不规则的立体图形,不能用公式直接计算。可以把两个完全一样的学具拼成一个圆柱,这样用圆柱的体积除以2就能求出学具的体积。如图:‎ ‎　　3.14×(16÷2)2×(24+26)÷2‎ ‎　　=3.14×64×50÷2‎ ‎　　=5024(cm3)‎ ‎　　答:它的体积是5024 cm3。‎ ‎【经验总结】‎ ‎ 解答此题的关键是把两个完全相同的不规则立体图形拼成一个圆柱,然后用圆柱的体积除以2就是所求的问题。‎ - 5 -‎ - 5 -‎ ‎【基础题】‎ ‎1.白兔和黑兔共有120只,黑兔的只数是白兔的,黑兔有多少只?‎ ‎2.学校体操队有甲、乙两个组,甲组人数是乙组的,甲组调3人给乙组后,甲组人数是乙组的,学校体操队共有多少人?‎ ‎3.一个长方体棱长总和是104 cm,长与宽的比是4︰3,长与高的比是2︰3。这个长方体的底面积是多少?‎ ‎4.在一个底面半径为15 cm的圆柱形容器中,有一块底面半径为10 cm的圆柱形钢材完全浸没于水中,当钢材取出后,容器内的水面下降2 cm,这块钢材的高是多少?‎ ‎【能力题】‎ ‎5.有一堆煤,第一天运走全部的,第二天运走剩下的,这时还剩15 t。这堆煤原有多少吨?‎ - 5 -‎ - 5 -‎ ‎6.某工厂甲、乙两车间人数的比是2︰5,如果从乙车间调18人到甲车间,两车间人数刚好相等。原来甲、乙车间各有多少人?‎ - 5 -‎ - 5 -‎ 参考答案 ‎1.120×=50(只)‎ ‎2.3÷=105(人)‎ ‎3.2∶3=4∶6‎ 长∶宽∶高=4∶3∶6‎ ‎104÷4=26(cm)‎ ‎×=48(cm2)‎ ‎4.3.14×152×2÷(3.14×102)=4.5(cm)‎ ‎5.×=‎ ‎15÷=150(t)‎ ‎6.18÷=84(人)‎ 甲车间:84×=24(人)‎ 乙车间:84×=60(人)‎ - 5 -‎ - 5 -‎