六年级上册数学教案 圆的面积 北京版 (5)

六年级上册数学教案 圆的面积 北京版 (5)

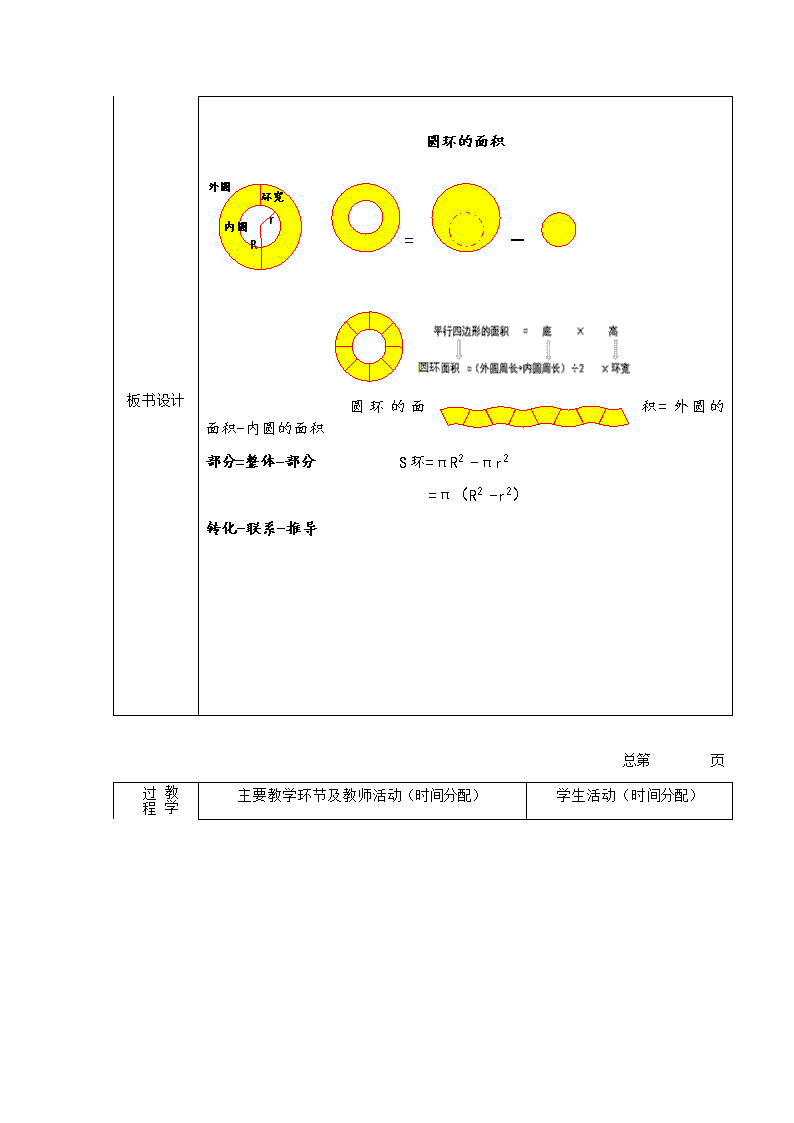
教 案 总第 页 课题 ‎　圆环的面积 授课时间 ‎ 12 月 8 日 ‎（星期 五 ）‎ 课型 ‎　新授 第 1课时（共1课时）‎ 教学目标 ‎1．通过观察、剪圆环等活动，了解圆环的特征，推导出圆环面积的计算公式“外圆的面积-内圆的面积”；迁移圆面积公式推导的方法，学生通过剪、拼、摆等活动，探究出圆环面积的另一种求法。‎ ‎2．通过操作、观察、比较、推理等活动，培养学生的观察能力、动手操作能力和语言表达能力，渗透转化思想、极限思想。‎ ‎3．在小组合作交流过程中，培养学生积极参与、主动探索及乐于分享、敢于质疑的精神，在参与中体验成功的乐趣。‎ 教学重点 了解圆环的特征，探究圆环面积的计算公式。‎ 教学难点 采用转化的方法探究圆环面积公式的推导过程。‎ 教学资源 多媒体课件、彩纸、圆环纸片、剪刀、磁力圆环教具等。　‎ 板书设计 圆环的面积 R r 环宽 外圆 内圆 ‎ = －‎ 圆环的面积=外圆的面积-内圆的面积 部分=整体-部分 S环=πR2 -πr2‎ ‎=π（R2 -r2）‎ 转化-联系-推导 ‎ ‎ ‎ ‎ 总第 页 主要教学环节及教师活动（时间分配）‎ 学生活动（时间分配）‎ 教学过程 一、认识圆环：（15分钟）‎ ‎1. 出示“光盘”图、“玉环”图，观察特点，抽象出圆环，初步认识圆环。‎ 同学们，今天这节课，我们学习《圆环的面积》，说说看到这个课题，你最想知道什么？‎ ‎ （1）这两个图形有什么共同的特点？‎ 这两个圆之间的部分就构成了一个圆环。‎ ‎（2）生活中你还在哪见到过圆环？‎ 生活中的圆环无处不在，你们看（课件呈现生活中的圆环）磁铁的截面是圆环形的、过街天桥的地面是圆环形的、砂轮的截面是圆环形的、天安门广场的花坛的形状也是圆环形的。看来，只要我们热爱生活，留心观察，一定还会有更多的发现。‎ ‎2．（出示圆形的纸片）这是个圆形纸片，请同学们先自已画一画，再剪出一个圆环。‎ ‎（展示学生的作品，深入了解圆环的特征。）‎ ‎（1）谁来汇报一下，你是怎样剪的呢？‎ ‎ 师：对他的方法有什么疑问吗？‎ 这两个圆有一个共同的圆心，我们管这样的两个圆叫作同心圆。两个同心圆之间的部分就是一个圆环。‎ ‎（2）这些都是圆环吗？说说你的理由。‎ ‎ ‎ ‎（3）交流：圆环有怎样的特征？什么样的图形是圆环？‎ 小结：圆环两个圆之间的距离处处相等，两个同心圆之间的部分形成了圆环。‎ ‎3.我们是通过观察，发现两个圆之间的距离相等的，怎样证明两个圆间的距离处处相等呢？‎ 师：那就折一折，通过折，又发现了什么？‎ ‎4.（黑板上画一个圆环）介绍圆环的各部分名称：外圆、内圆、外圆半径、内圆半径、环宽。外圆半径、内圆半径、环宽三者有怎样的关系呢？‎ 课件 小结：三者的关系也就是部分与整体之间的关系。（板书：部分=整体-另一部分）‎ 下面给出了圆环的“外圆半径、内圆半径、环宽”中的两个，请求出另一个是多少？说一说三者之间的关系。‎ 二 、探究圆环面积公式：（15分钟）‎ 1. 圆环面积公式的一般推导方法。‎ 想一想 说一说：‎ ‎（1）回顾剪圆环的过程，思考：怎么求圆环的面积呢？‎ ‎（2）如何用字母表示公式？‎ ‎（3）把你的想法说给同桌听一听。‎ ‎ ‎ ‎ 全班进行交流，教师进行板书。‎ 2. 圆环面积公式的另一种推导方法。‎ 我们通过剪圆环的过程，发现圆环的面积等于外圆的面积减内圆的面积，你看，又是通过部分与整体的关系来解决的问题。‎ 还有其它的推导方法吗？‎ 以前有个学生曾经问我：平行四边形、三角形、梯形、圆形公式的推导过程，都是经历了“转化图形—建立联系—推导公式”的过程进行推导出来的，圆环的面积公式也采用这种推导方法行吗？‎ 探究要求：‎ ‎（1）通过动手折一折、剪一剪、拼一拼，转化成新图形，尝试推导圆环的面积计算公式。‎ ‎（2）把研究成果先在组内说一说，做好汇报、补充答疑的准备。‎ 学生汇报 师：（课件）经过同学们的研究，我们把圆环平均分成了8份，转化成了近似的平行四边形；平均分成16份，转化成了这样的平行四边形；想象一下，如果平均分成32份，能拼成一个什么样的平行四边形？平均分成64份呢？128份呢？无限多的份呢？分得无限多的话，拼成的图形就是一个平行四边形或者说就是一个标准的长方形了，这就是极限思想。以后我们还会进一步的学习。‎ 这个公式和我们刚才推导出的公式有联系吗？我们一起来看，课件进一步的进行推导。得到 S环=πR2 -πr2‎ S环=π（R2 -r2）‎ ‎3.总结方法，深入认识：同学们，通过“转化—联系—推导”的数学思想和方法，我们找到了计算圆环面积的新方法。‎ 其实，转化这种方法在以前的学习中经常用到，如我们将小数乘法转化为整数乘法，从而得到了小数乘法的计算方法；我们将异分母分数加减法转化为同分母分数加减法，从而得到了异分母分数加减法的计算方法。‎ 在今后的学习中，“转化”这种数学思想方法，我们还会多次用到。看来知识之间是存在联系的，希望同学们遇到新问题能够认真思考，运用已有的知识和方法解决新问题。‎ 三、解决问题，提升能力：（8分钟）‎ 试一试： 一个圆圆环的草编茶杯垫，外圆半径是5厘米，中间是一个半径为2厘米的圆孔（如图）。这个茶杯垫正面的面积是多少平方厘米？‎ ‎ ‎ 学生读题后，独立解决，展示汇报，说说自己的想法。‎ 小结：有了圆环面积的计算公式，我们很容易的解决了这个问题。‎ ‎ ‎ 问题一：如图，光盘上有一部分涂着黄色。求涂黄色部分的面积是多少平方厘米？（图中单位：厘米）‎ 读题后，追问：解决这个问题的关键是先求什么？谁口述一下这个题的解决方法？‎ 小结：通过直径求出半径，转化成了第一题的形式，轻松的就解决了这个问题。‎ 问题二：一个圆形鱼池，鱼池的中心是一个圆形小岛（如图）。求鱼池水面的面积。‎ 读题后，追问：解决这个问题的关键是先求什么？ ‎ 六、课堂总结：（2分钟）‎ 回顾这节课的学习，说说，你有哪些收获？‎ 生：什么是圆环？圆环的面积该怎样计算呢？‎ 生：有两个圆，一个大圆一个小圆。‎ 生：如机器零件、胶条的截面 生：汇报方法和过程 生：你是怎样找到这个圆的圆心的呢？‎ 生：对折打开，再对折再打开，两条折痕的交点就是圆心。‎ 生：前3个是圆环，最后一个不是圆环，因为内圆到外圆的距离不相等。‎ 生：两个同心圆之间的部分是圆环；圆环两个圆之间的距离处处相等。‎ 生：可以量一量；可以对折重合；因为是同心圆，都是大圆的直径减去小圆的直径，所以相等。‎ 生：圆环也是轴对称图形，有无数条对称轴。‎ 生：环宽=外圆直径-内圆直径 生：‎ ‎（1） R–r=环宽 ‎ 20-9=11cm ‎（2） R–环宽=r ‎ 20-17=3cm ‎（3）环宽+ r =R ‎ 9+11=20 cm 学生自己探究圆环面积公式的求法，先在小组内交流，然后全班交流汇报。‎ 生：圆环的面积=外圆的面积-内圆的面积 S环=πR2 -πr2‎ S环=π（R2 -r2）‎ 生通过剪、拼、转化图形来尝试推导圆环的面积公式,‎ 生操作：‎ 学生独立解决，并交流想法。‎ ‎3.14×52 -3.14×22‎ ‎= 78.5–12.56‎ ‎= 65.94(平方厘米) ‎ ‎ 3.14×（52 - 22） ‎ ‎= 3.14×21‎ ‎= 65.94(平方厘米) ‎ ‎12÷2=6（厘米）‎ ‎4÷2=2（厘米）‎ ‎3.14×62 -3.14×22 ‎ ‎= 113.04－12.56‎ ‎= 100.48(平方厘米) ‎ ‎3.14×（62 - 22） ‎ ‎= 3.14×32‎ ‎= 100.48(平方厘米) ‎ 生：没有半径，先求出半径。‎ 学生独立解决，并交流想法。‎ ‎ 6÷2=3（米）‎ ‎3＋5=3（米）‎ ‎3.14×82－3.14×32 ‎ ‎= 200.96－28.26‎ ‎= 172.7(平方米) ‎ ‎3.14×（82 - 32） ‎ ‎= 3.14×55‎ ‎= 172.7(平方米) ‎ 生：怎么求外圆的半径？‎ 生：求出外圆的直径再求半径；或用环宽加内圆的半径求外圆的半径。‎ 教学反思 ‎ ‎ 围绕“课改背景下，构建知行合一育人课堂”、“打造生本课堂，提升学生核心素养”的课题研究。落实“以学生的发展为本”的理念，把探究与交流做为课堂教学的主要方式，在“自主探索、合作交流”中学习知识，提升能力。‎ 学过的几个平面图形，学生都是经历了“转化图形—建立联系—推导公式”的方法得到的面积公式，为什么到圆环就“只能用大圆的面积减去小圆的面积”了呢？学生产生了这样的疑惑，原来的探究方法还行吗？学生的疑问是研究最好的动力。‎ 基于以上认识，本节课的教学内容增加了“认识圆环，通过转化图形的方法探究圆环面积的公式”，学生利用已有的方法，通过剪、拼、摆等活动，探索出圆环的面积公式。学生在小组合作探究、交流与分享中，理解和掌握了基本的数学知识与技能，体会运用了数学思想与方法，获得了基本的数学活动经验，推理能力得到了较好的发展。教学过程突出了学生的主体地位，在师生、生生互动与对话中，让学生真正成为了学习的主体。‎