五年级上册数学北京课改版知识要点

五年级上册数学北京课改版知识要点

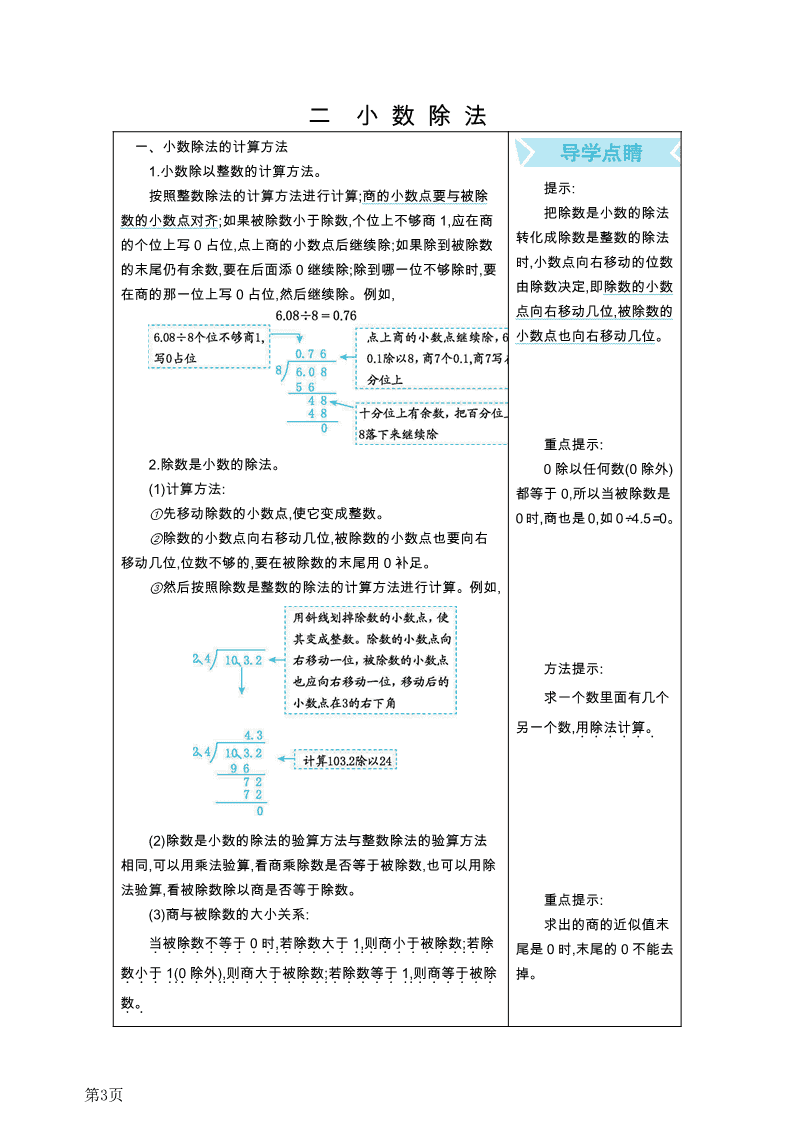
一 小 数 乘 法 一、小数乘整数 1.积的变化规律: (1)一个因数不变,另一个因数扩大到原 来的几倍(或缩小到原来的几分之几),它们的 积也扩大到原来的几倍(或缩小到原来的几 分之几)。 (2)如果一个因数扩大到原来的几倍,另 一个因数缩小到原来的几分之几 ,它们的积 不变。 2.小数乘整数的计算方法: 先按整数乘法算出积,再看因数中一共 有几位小数,有几位小数,就从积的右边起数 出几位,点上小数点。如果积的小数部分末尾 有 0,可以把 0去掉,把小数化简。 二、小数乘小数 1.小数乘小数的计算方法: (1)按照整数乘法的计算方法算出积。 (2)看因数中一共有几位小数,有几位小 数,就从积的右边起数出几位,点上小数点。 (3)如果积的小数位数不够,就在积的前 面用 0补位。 (4)如果积的小数部分末尾有 0,可以把 0 去掉。 2.因数与积的大小关系: 一个因数大于．．．．．．1．,．积大于另一个因数．．．．．．．．(．0．除． 外．);． 一个因数小于．．．．．．1．,．积小于另一个因数．．．．．．．．(．0．除． 外．)． 一个因数等于．．．．．．1．,．积等于另一个因数。．．．．．．．．． 三、小数乘法的估算及积的近似值 1.小数乘法的估算方法: 先用“四舍五入法”把两个因数分别看作 与它接近的整数,再把这两个整数相乘即可 估算出积。 2.在估算过程中,看作的整数如果比原来 重点提示: 小数乘整数的意义与整数乘法的意义相．．．．．．．．．．．．．．．．． 同．,．都是求几个相同加数的和的简便运算。 要点提示: 小数乘整数的积的末尾有0时,一定要先． 点积中的小数点．．．．．．．,．再去掉小数部分末尾的．．．．．．．．．．0．。． 知识巧记: 小数乘法并不难, 关键点好小数点; 因数小数位数和, 等同积中小数位; 积中位数如不够, 用 0补足再点点; 如果因数不为 0, 一个因数大于 1, 另一个因数小于积; 一个因数小于 1, 另一个因数大于积。 知识巧记: 四舍五入方法好, 近似值来有法找; 保留哪位看下位, 再同数 5作比较; 第1页 的因数大,积的估算值大于准确值;看作的整 数如果比原来的因数小,积的估算值小于准 确值。 3. 由于估算所得的结果不是积的准确 值,因此应该用“≈”连接。 4.求得的近似值如果是末尾有 0的小数, 这个小数末尾的0不能去掉,否则会改变精确 度。 四、小数混合运算 小数混合运算的运算顺序: 1.在没有括号的算式里,要先算乘除法, 后算加减法。 2.在只有小括号的算式里,要先算小括号．．．．． 里面的．．．,．再算小括号外面的。．．．．．．．．． 3.在同时有小括号和中括号的算式里,要． 先算小括号里面的．．．．．．．．,．再算中括号里面的．．．．．．．．,．最后．． 算中括号外面的。．．．．．．．． 五、小数乘法的简算 1.运算定律: 乘法交换律:a×b=b×a 乘法结合律:(a×b)×c=a×(b×c) 乘法分配律:(a+b)×c=a×c+b×c 减法的性质:a-b-c=a-(b+c) 2.整数乘法的运算定律对于小数乘法同 样适用,运用乘法运算定律和减法的性质可 以使小数混合运算计算起来更简便。 六、用小数乘法解决实际问题 运用小数乘法的知识解决实际问题时, 先要找出已知条件和所求问题,然后分析题 中的数量关系,最后确定解题方法。 是 5大 5前进 1, 不足 5的全舍掉; 等号改成约等号, 使人一看就明了。 方法提示: 小数混合运算的运算顺序与整数混合运 算的运算顺序相同。 知识巧记: 小数简算并不难, 运算定律莫记乱; 交换、分配和结合, 算完还要再细看。 重点提示: 乘法分配律的逆用: a×c+b×c=(a+b)×c 方法提示: 可以用树状图表示题中的数量关系,理 清解题思路。 第2页 二 小 数 除 法 一、小数除法的计算方法 1.小数除以整数的计算方法。 按照整数除法的计算方法进行计算;商的小数点要与被除 数的小数点对齐;如果被除数小于除数,个位上不够商 1,应在商 的个位上写 0占位,点上商的小数点后继续除;如果除到被除数 的末尾仍有余数,要在后面添 0继续除;除到哪一位不够除时,要 在商的那一位上写 0占位,然后继续除。例如, 2.除数是小数的除法。 (1)计算方法: ①先移动除数的小数点,使它变成整数。 ②除数的小数点向右移动几位,被除数的小数点也要向右 移动几位,位数不够的,要在被除数的末尾用 0补足。 ③然后按照除数是整数的除法的计算方法进行计算。例如, (2)除数是小数的除法的验算方法与整数除法的验算方法 相同,可以用乘法验算,看商乘除数是否等于被除数,也可以用除 法验算,看被除数除以商是否等于除数。 (3)商与被除数的大小关系: 当被除数不等于．．．．．．．0．时．,．若除数大于．．．．．1．,．则商小于被除数．．．．．．．;．若除．． 数小于．．．1．(．0．除外．．),．则商大于被除数．．．．．．．;．若除数等于．．．．．1．,．则商等于被除．．．．．． 数。．． 提示: 把除数是小数的除法 转化成除数是整数的除法 时,小数点向右移动的位数 由除数决定,即除数的小数 点向右移动几位,被除数的 小数点也向右移动几位。 重点提示: 0 除以任何数(0 除外) 都等于 0,所以当被除数是 0时,商也是0,如0÷4.5=0。 方法提示: 求一个数里面有几个 另一个数,用除法计算。．．．．．． 重点提示: 求出的商的近似值末 尾是 0时,末尾的 0不能去 掉。 第3页 3.商的近似值。 (1)取商的近似值的方法:先看保留几位小数．．．．．．．．,．保留几位小数．．．．．．,． 就除到比需要保留的小数位数多一位．．．．．．．．．．．．．．．．,．再按照．．．“．四舍五入法．．．．．”．取商．． 的近似值。．．．．． (2)用“进一法”解决实际问题。 “进一法”:在解决问题时,根据实际情况,不管省略部分最高．．．．．．．． 位上的数字是多少．．．．．．．．,．都要向前一位进．．．．．．．1．。．用“进一法”得到的近似 值比准确值大。 (3)用“去尾法”解决实际问题。 “去尾法”:在解决问题时,根据实际情况,不管省略部分最高．．．．．．．． 位上的数字是多少．．．．．．．．,．都要舍去。．．．．．用“去尾法”得到的近似值比准确 值小。 4.循环小数。 (1)一个小数的小数部分从某一位起,一个数字或者几个数．．．．．．．．． 字依次不断地重复出现．．．．．．．．．．,．这样的小数叫作循环小数。 例如,1.666… 1.1363636… (2)循环节。 一个循环小数的小数部分,依次不断重复出现的数字就是 这个小数的循环节。例如,在 1.666…中,“6”是小数部分依次不断 重复出现的数字,“6”就是这个循环小数的循环节;在 1.1363636…中,“36”是小数部分依次不断重复出现的数字,“36” 就是这个循环小数的循环节。 (3)循环小数的简便写法。 ①循环节是一个数字的循环小数,可以只写一个循环数字,并 在这个数字的上面记一个小圆点,如 1.666…写作:1. 。 易错题: 5.7÷9≈0.6333… 错解分析:商 0.6333…是循环小数,它 是一个准确值,不能用“≈” 连接。 正确答案: 5.7÷9=0.6333… 易错题: 98989898.9898 是循 环小数。(√) 错解分析:题中所给的 数虽然是由 9和 8 两个数 字重复组成的,但是这两个 数字在小数部分只重复出 现了两次,小数部分是四位 小数,这是一个有限小数。 正确答案:✕ 点拨: 循环小数的小数部分．．．．．．．．． 的位数是无限的．．．．．．．,．而这个小．．．． 数的整数部分的位数是有．．．．．．．．．．． 限的。．．． 第4页 ②循环节是多个数字的循环小数,可以只写一组循环数字, 并在这组循环数字的首位数字和末位数字上面各记一个小圆 点,如 1.1363636…写作:1.1 ; 3.5437437…写作:3.5 3 。 (4)拓展提高。 纯循环小数:循环节从小数部分的十分位开始的小数叫作．．．．．．．．．．．．．．．．．．． 纯循环小数。．．．．．．例如,5. ,2.777…。 混循环小数:循环节不是从小数部分的十分位开始的小数．．．．．．．．．．．．．．．．．．． 叫作混循环小数。．．．．．．．．例如,2.18585…。 (5)取循环小数的近似值的方法: 可以用“四舍五入法”取循环小数的近似值。 二、解决问题 在解决实际问题的过程中,要准确找出题中的信息,根据题 中的信息分析数量关系,找出解题策略。 三、探索规律:揭示除法中的秘密 被除数和除数．．．．．．(．均不为．．．0．)．交换位置后．．．．．,．所得的商和原商相乘．．．．．．．．．,． 积都等于．．．．1．。．用字母表示:如果 a÷b=m,b÷a=n(a、b均不为 0), 那么 m×n=1。 方法提示: 理清题目中的数量关 系是解题关键。 要点提示: (a÷b)×(b÷a) =a÷b×b÷a =1 a、b 均不为 0。 第5页 三 平行四边形、梯形和三角形 一、平行四边形 1.平行四边形的定义。 两组对边分别平行的四边形叫作平行四边形。 2.平行四边形的基本特征。 平行四边形的两组对边分别平行且相等。 3.长方形、正方形和平行四边形之间的关系。 长方形和正方形同平行四边形一样,都是两组对边分别平 行且相等,长方形和正方形具有平行四边形的一切特征,所以 长方形和正方形都是特殊的平行四边形。正方形不仅具备长 方形的所有特征,并且四条边都相等,所以正方形是特殊的长 方形。 4.平行四边形的特性。 平行四边形具有不稳定性,容易变形。 5.平行四边形的面积。 (1)认识平行四边形的底和高。 从平行四边形一条边上的任意一点向对边引垂线,这点到 垂足间的线段叫作平行四边形的高,垂足所在的边叫作平行四 边形的底。平行四边形有无数条高,一般能画出两种长度的高。 (2)平行四边形的面积。 通过剪拼发现:长方形的面积与平行四边形的面积相等, 重点提示: 在拉动长方形的过程 中,长方形的形状改变,但两 组对边的长度不变。 易错题: 平行四边形的对边一定 相等,邻边一定不相等。( ) 错解分析:此题错在对 平行四边形的特征理解不准 确,平行四边形一定具备对 边相等的特征,但对邻边没 有要求,所以平行四边形的 邻边也可以相等。 正确答案:✕ 重点提示: 平行四边形的底和高是 一组相互依存且对应的概念 (底边上的高,高所对应的 底)。 易错题:周长相等的两 第6页 平行四边形的底等于长方形的长．．．．．．．．．．．．．．;．平行四边形的高等于长方形．．．．．．．．．．．． 的宽．．。 长方形的面积=长×宽 平行四边形的面积=底×高 如果用 S表示平行四边形的面积,a 和 h分别表示平行四 边形的底和高,那么平行四边形的面积的字母公式为 S=ah。 二、梯形 1.梯形的定义。 只有一组对边平行的四边形叫作梯形。 2.平行四边形和梯形的异同点。 相同点:都是四边形;都有平行的对边。 不同点:平行四边形的两组对边分别平行且相等;梯形只 有一组对边平行,且平行的这组对边不相等。 3.认识梯形各部分的名称。 在梯形中,互相平行的一组对边分别叫作梯形的上底和下 底;不平行的一组对边叫作梯形的腰。从上底的任意一点向下 底引垂线,这点到垂足间的线段叫作梯形的高。 4.认识直角梯形和等腰梯形。 (1)直角梯形。 有一个角是直角的梯形叫作直角梯形。 (2)等腰梯形。 两腰相等的梯形叫作等腰梯形。 等腰梯形是轴对称图形,它只有一条对称轴;直角梯形不 是轴对称图形。 5.梯形的面积。 个平行四边形,面积也相等。 (√) 错解分析:平行四边形 的面积是由底和高共同决定 的,两个平行四边形的周长 相等,它们的底和高的乘积 却不一定相等,因此面积不 一定相等。 正确答案:✕ 易错题:有一组对边平 行的四边形是梯形。(√) 错解分析:此题错在没 有掌握梯形的特征。“有一组 对边平行”和“只有一组对边 平行”要注意区分,题中没有 强调“只有一组对边平行”,所 以是错的。 正确答案:✕ 重点提示: 一个直角梯形有两个直 角。 第7页 两个完全一样的梯形可以拼成一个平行四边形。平行四 边形的底等于梯形的上、下底之和,高等于梯形的高。每个梯 形的面积等于这个平行四边形面积的一半。 平行四边形的面积=(上底+下底)×高,所以梯形面积=(上 底+下底)×高÷2。 如果用 a、b、h、S分别表示上底、下底、高和面积,则 S=(a+b)×h÷2。 6.梯形面积计算公式的应用。 (1)已知梯形的上底、下底和高,可以直接运用梯形的面积 公式来计算,即梯形的面积．．．．．=．(．上底．．+．下底．．)．×．高．÷．2．。． (2)高=面积×2÷(上底+下底) 上底+下底=面积×2÷高 三、三角形 1.三角形的含义和各部分的名称。 (1)三角形的含义。 由三条线段顺次首尾相接组成的图形叫作三角形。 (2)三角形各部分的名称。 三角形有三条边、三个顶点和三个角。 (3)三角形的特性。 三角形具有稳定性,不易变形。 (4)三角形三条边之间的关系。 三角形任意两边的和大于第三边。．．．．．．．．．．．．．．． 2.三角形的分类。 (1)三角形按角分类: 锐角三角形:三个角都是锐角的三角形叫作锐角三角形。 直角三角形:有一个角是直角的三角形叫作直角三角形。 钝角三角形:有一个角是钝角的三角形叫作钝角三角形。 (2)三角形按边分类。 不等边三角形:三条边都不相等的三角形叫作不等边三角 要点提示: 等腰梯形的两腰相等．．．．．．．．．,． 两个底角也相等。．．．．．．．． 易错题: 两个面积相等的梯形一 定可以拼成一个平行四边 形。(√) 错解分析:两个梯形面 积相等,上底、下底和高不一 定相等,所以面积相等的梯 形不一定能拼成平行四边 形。完全相同的两个梯形才 能拼成一个平行四边形。 正确答案:✕ 易错题:由三条线段组 成的图形叫作三角形。(√) 错解分析:由三条线段 组成的图形不一定都是三角 形,由三条线段顺次首尾相 接组成的封闭图形才是三角 形。 正确答案:✕ 重点提示: 在一个三角形中至少有．．．．．．．．．． 两个角是锐角。．．．．．．． 第8页 形。 等腰三角形:有两条边相等的三角形叫作等腰三角形。 等边三角形:三条边都相等的三角形叫作等边三角形。 (3)等边三角形的三个角都是 60°。等边三角形和等腰三角．．．．．．．．．． 形都是轴对称图形。．．．．．．．．． (4)拓展提高。 在一个三角形中,相等的边所对的角一定相等;反之,如果 两个角相等,那么它们所对的边一定也相等。 3.三角形的内角和。 (1)三角形的内角和定理。 通过观察发现:锐角三角形和钝角三角形各自拼成了一个 平角。直角三角形的两个锐角拼起来和它的直角相等,三个角 的度数相加的和是 180°。 (2)三角形的内角和定理的应用。 已知三角形两个内角的度数,根据三角形的内角和等于 180°,用内角和 180°连续减去已知的两个角的度数,即可求出 第三个角的度数。 在直角三角形中,已知一个锐角的度数,可以直接用 90°减 去已知锐角的度数,即可求出另一个锐角的度数。 4.三角形的面积。 (1)三角形的底和高。 从三角形的一个顶点向它的对边作一条垂线,顶点到垂足 之间的线段叫作三角形的高,垂足所在的边叫作三角形的底。 任意一个三角形都有三条高。 (2)三角形面积公式的推导。 易错提示: 等边三角形一定是等腰 三角形,但等腰三角形不一 定是等边三角形。 易错题: 三角形中两个锐角的度 数和一定大于 90°。(√) 错解分析:这个结论只 适用于锐角三角形,在直角 三角形和钝角三角形中不成 立。 正确答案:✕ 点拨: 钝角三角形中两个锐角 的度数和小于 90°,直角三角 形中两个锐角的度数和等于 90°。 画法提示: 画高时必须由顶点向它 的对边画垂线,当对边不够 长时,可以画虚线将对边延 第9页 两个完全一样的三角形可以拼成一个平行四边形。．．．．．．．．．．．．．．．．．．．．．． 平行四边形的底=三角形的底 平行四边形的高=三角形的高 平行四边形的面积=底×高 三角形的面积=底×高÷2 用 S 表示三角形的面积,a 表示底,h 表示高,则 S=ah÷2。 (3)三角形面积公式的应用。 三角形的高 h=2S÷a 三角形的底 a=2S÷h 四、组合图形 1.认识组合图形。 组合图形是由简单图形组合而成的。 2.组合图形的面积。 计算组合图形的面积时,要根据已知条件对图形进行分 解,先转化成已学过的简单图形,分别计算出它们的面积,再求 和或求差。 五、千米 2和公顷 1.认识千米 2和公顷。 (1)千．米． 2．和公顷是常用的测量较大土地面积的计量单位．．．．．．．．．．．．．．．．．．．．。． (2)边长．．是．10．．0．米的正方形的面积．．．．．．．．是．1．公顷．．;．边长．．是．1．千米．． (．1000．．．．米．)．的正方形的面积是．．．．．．．．1．千米．． 2．。． 2.公顷和千米 2之间的进率。 1公顷=10000 米 2 1 千米 2=100 公顷=1000000 米 2 3. 千米 2、公顷、米 2之间的换算方法。 千米2换算成公顷,把小数点向右移动两位,反之,向左移动 两位;公顷换算成米 2,把小数点向右移动四位,反之,向左移动 四位;千米 2换算成米 2,把小数点向右移动六位,反之,向左移动 六位。 长。所画的高用虚线表示．．．．．．．．．,． 并标上直角符号。．．．．．．．． 易错题: 三角形的面积等于平行 四边形面积的一半。(√) 错解分析:此题错在没 有强调三角形与平行四边形 等底等高这一条件。 正确答案:✕ 提示: 计算每个简单图形的面 积时,要找准对应的数据。 方法提示: 由高级单位换算成低级 单位,要乘进率;由低级单位 换算成高级单位,要除以进 率。 第10页 四 统计图表与可能性 一、统计表 1.认识复式统计表。 某电器连锁店2011年四种家用电器销售情况统计 表 2012年 2月 为了便于分析和比较,有时需要把几个有联系 的简单统计表合并成一个比较复杂的统计表,即复 式统计表。 是表头,店别表示竖栏的类别;种 类表示横栏的类别,即四种家用电器的名称;销售额 /万元表示栏中的数据。 “合计”是指两家分店每种家用电器的销售总 额。 2.简单统计表和复式统计表的联系与区别。 区别:简单统计表只对某一项目的数量进行统．．．．．．．．．．．．．．．．． 计．;．复式统计表的统计项目在两个或两个以上。复．．．．．．．．．．．．．．．．．．．． 式统计表的表内部分比简单统计表的表内部分复．．．．．．．．．．．．．．．．．．．．． 杂。．． 联系:都分为表外和表内两部分．．．．．．．．．．．,．表外部分都包．．．．．． 提示: 如果表头中已标明单位 名称,填写栏中数据时不需要 加单位名称;如果没有标明, 填写栏中数据时,数据后要加 单位名称。 重点提示: 计算时,将同一竖栏中的 数据合在一起,填在对应竖栏 的合计处。 方法总结: 第11页 括统计表的名称和制作时间。．．．．．．．．．．．．． 二、平均数 求较复杂的平均数的方法: 先求出每组数据的总数量．．．．．．．．．．．(．用每组数据的平均．．．．．．．． 数．×．数据个数．．．．),．然后求出全部数据的总数量及总份．．．．．．．．．．．．．．． 数．,．最后用．．．“．总数量．．．÷．总份数．．．”．求出平均数。．．．．．． 三、统计图 认识并绘制复式统计图: 1.复式条形统计图: 用两种(或两种以上)直条表示不同数量的条形 统计图,称为复式条形统计图。 2.复式条形统计图的绘制方法: 与单式条形统计图的绘制方法基本相同,只是 每组中表示两组(或两组以上)数据,需要用不同颜 色(或底纹)的直条来表示,同时要注明图例。 3.复式条形统计图的作用: 不仅可以清楚地反映出各组数量的多少．．．．．．．．．．．．．．．．．,．还可．． 以把各组数量进行对比．．．．．．．．．．,．从而获取更多的信息。．．．．．．．．．． 总数量÷总份数=平均数 平均数×总份数=总数量 总数量÷平均数=总份数 提示: 1.画直条时,一般先画一 种直条,再画另一种直条。 2.在绘制复式条形统计 图时,要写出统计图的名称和 制图时间,并注明图例,图中．． 的直条宽窄要相同．．．．．．．．,．单位长度．．．． 要统一。．．．． 重点提示: 事件发生的可能性存在．．．．．．．．．． 确定性和不确定性。．．．．．．．．． 第12页 四、可能性 判断事件发生的可能性: 1.事件发生的可能性的大小与物体数量的多 少有关。物体在总数中所占的数量越多．．．．．．．．．．．．．,．发生的可．．．． 能性越大．．．．,．所占的数量越少．．．．．．．,．发生的可能性越小。．．．．．．．．． 2.事件发生的可能性的大小能反映出物体数 量的多少。可能性大,对应的物体数量相对较多。 第13页 五 方 程 一、用字母表示数 1.用字母可以表示数,用含有字母的式子也可以表 示数。 2.含有字母的式子的简便写法。 在含有字母的式子里,数和字母、字母和字母相乘 时,乘号可以省略不写。省略乘号时,数字要写在字母的 前面,数字是 1时,可以省略不写。例如,1×x 可以写成 x;3×x 可以写成 3x;8×b 可以写成8b;a×a可以写成 a2, 读作 a的平方,表示两个 a相乘。 3.用含有字母的式子表示数量关系并求值。 (1)用含有字母的式子可以表示数量关系,当字母 的值确定时,含有字母的式子的值也随之确定。 (2)求含有字母的式子的值时,将字母的值代入原 式,直接计算求出得数即可。 二、方程 1.等式和方程。 (1)认识等式。 把相等的量、式子或数用等号连接起来就成了等．．．．．．．．．．．．．．．．．．．．． 式。．． 例如,329-9=180+140 3a=9b a-8=b+9 (2)等式的基本性质。 等式的基本性质:等式两边都加上．．．．．．．(．或减去．．．)．同一个．．． 数．,．左右两边仍然相等．．．．．．．．;．等式两边都乘同一个数．．．．．．．．．．(．或除以．．． 同一个不为．．．．．0．的数．．),．左右两边仍然相等。．．．．．．．．． (3)方程的意义。 含有未知数的等式叫作方程。．．．．．．．．．．．．． (4)方程与等式的关系。 所有的方程都是等式,但等式不一定是方程。 易错题: a2=(2)×(a) 错解分析: a2表示两个 a相乘,不表示 a的 2 倍,应是 a×a。 正确答案: a2=(a)×(a) 方法提示: 将数据代入原式求值时,原来含 有字母的式子中被省略的乘号要还 原。 易错题: 3x+12 是方程。(√) 错解分析: 3x+12 中虽然含有未知数,但只 是一个式子,并不是等式,因此不是 方程。 正确答案:✕ 重点提示: 方程必须具备两个条件: 1.是等式。．．．． 2.含有未知数。．．．．．． 提示: 方程的解中的“解”是名词,是一 个数值;解方程中的“解”是一个动词, 第14页 2.解方程。 (1)用等式的基本性质解一步方程 ①一步方程可以直接利用等式的基本性质求解。 ②形如 ax=b(a≠0)的方程的解法。 ax=b 解:ax÷a=b÷a→根据等式的基本性质 x=b÷a ③使方程左右两边相等的未知数的值．．．．．．．．．．．．．．．,．叫作方程．．．． 的解．．;．求方程解的过程叫作解方程。．．．．．．．．．．．．． ④方程的检验:把求出的 x的值代入原方程,看方 程的左右两边是否相等,如果相等,则求出的 x的值是 方程的解;如果方程的左右两边不相等,则不是原方程 的解。 (2)用等式的基本性质解稍复杂的方程。 解稍复杂的方程,可以先将方程化简,再利用等式 的基本性质求解。 解形如 ax±bx=c(a±b≠0)的方程的解法。 ax±bx=c 解:(a±b)x=c (a±b)x÷(a±b)=c÷(a±b) x=c÷(a±b) 3.列方程解应用题。 列方程解应用题的步骤和方法: (1)弄清题意找出未知量,用 x 表示。 (2)找出题中的等量关系,列方程。 (3)解方程。 (4)检验并写出答语。 是指演算的过程。 重点提示: 解方程之前要先写“解”字,再计 算。解方程时等号要上下对齐,且每 一步得到的都是等式。 重点提示: 列方程时一般设 1倍量(即标准 量)为 x。 第15页 六 数学百花园 一、密铺。 1.认识密铺。 2.密铺的意义。 用正方形、长方形或其他形状的地砖铺地,可以使 它们彼此之间不留空隙、不重叠地铺成一片,通常把这 种铺法叫作密铺。 3.通过动手拼一拼可知:正方形、长方形、平行四 边形、正六边形等都可以单独密铺;用两种或两种以上 的不同的图形进行搭配也可以密铺;有一些不规则的 图形也可以密铺。 二、鸡兔同笼 1.“鸡兔同笼”问题。 “鸡兔同笼”问题是我国古代的趣味名题,出自古代 数学名著《孙子算经》,因其计算同一个笼中鸡和兔的 只数而得名。 2.“鸡兔同笼”问题的解法。 解答“鸡兔同笼”问题可以用画图法、列表法、假 设法、方程法。 假设法的过程是假设—计算—推理—解答。 假设全是鸡,则兔的只数=(实际腿数-鸡的只数 ×2)÷(4—2)。 假设全是兔,则鸡的只数=(兔的只数×4—实际腿 数)÷(4—2)。 方程法:根据头数和腿数之间的数量关系列出方 程进行解答。 重点提示: 多边形可以密铺的条件:拼接在 一起的边相等,围绕一点拼在一起的 多边形的内角加在一起恰好组成一 个周角。 重点提示: 用．“．假设法．．．”．求．“．鸡兔同笼．．．．”．问题时．．．,． 假设笼子里全是兔时．．．．．．．．．,．先求出的是鸡．．．．．． 的只数．．．;．假设笼子里全是鸡时．．．．．．．．．,．先求．． 出的是兔的只数。．．．．．．．． 第16页