- 2021-12-10 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
五年级下册数学教案-第6单元 打电话-人教版 (4)
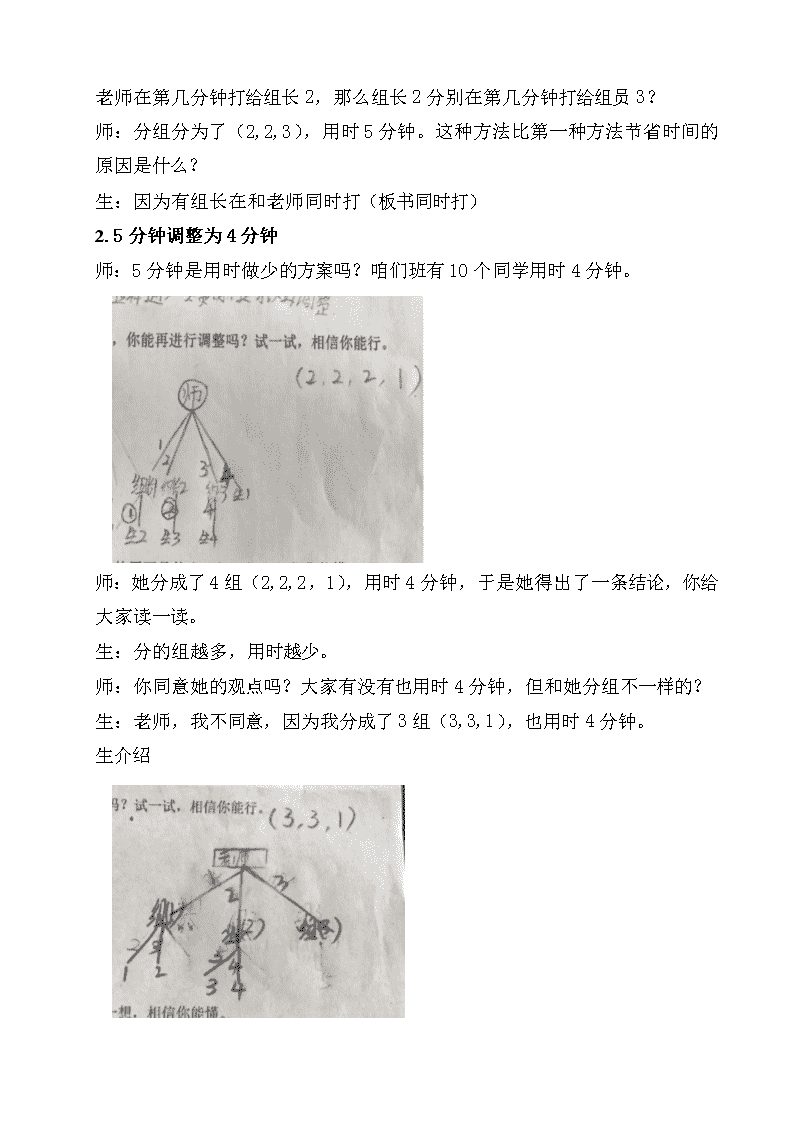
《打电话》 一、教学内容 人教版义务教育教科书五年级下册第七单元《打电话》 二、教材分析 (一)本节课与前后知识的联系 “打电话”所使用的素材是学生所熟悉的,问题和学生的生活经验密切结合,学生对这一问题的研究很有兴趣。“打电话”这一问题正是为学生提供了可探究的空间,学生尝试寻找“答案”时,不是简单地应用已知的信息,也没有可直接利用的方法、公式。尽管不是所有的学生最终都能出色地完成任务,但是他们都尽自己的思维能力“走”得足够远。很有让学生去研究的价值。 (二)教学目标 1、利用学生熟悉的生活情境,通过画图的方式,使学生找到打电话的最优方法; 2、渗透数形结合的思想,培养学生借助图形解决问题的意识; 3、进一步体会数学与生活的密切联系以及优化思想在生活中的应用, (三)教学重难点 1、教学重点:理解打电话的各个方案并从中优化出最好的方案。 2、教学难点:突破“知识本位”,让学生充分经历了解决问题的过程,体会到优化的思想。 三、学情分析: 这一内容安排在五年级下学期,从生活经验看,大多学生有通知多个人的生活经历,因此,已有的生活经验足以支持完成此任务。其次,从已有知识储备看,参与完成此任务虽涉及画图表达、计算等综合知识,但都是较简单的计算与表达。从思想方法看,在四年级上册的《数学广角》中教材已安排了有关优化思想的学习。 教学重点:绘制网络图设计最省时的打电话方案。 教学难点:通过观察网络图,探寻规律。 四、教学过程 (一)导入 师:课前老师给大家布置了打电话的任务(出示课件) 一个合唱队,共有7人。暑假期间有一个紧急演出,老师需要尽快的通知到每一个队员,为了让每一名队员都能收到消息,老师采用打电话的方式,而每通知一名队员需要1分钟。请你帮我设计一个打电话的方案。 师:在这个数学问题中,你觉得哪些信息比较关键?对于通知有什么要求? 师:我看了大家的预学单,大部分人想到了这样的7分钟方法,你们觉得这种方法不符合哪个要求? 师:然后大家都调整了自己的方案,用时也不一样,大家先在小组内交流自己的想法,组织一下语言,想想怎样才能给大家讲明白。 组内交流 (二)展示 1.7分钟调整为5分钟 生介绍(2,2,3) 引导语言:谁第几分钟给谁打电话? 师:老师在第几分钟打给组长1,那么组长1分别在第几分钟打给组员1,2?老师在第几分钟打给组长2,那么组长2分别在第几分钟打给组员3? 师:分组分为了(2,2,3),用时5分钟。这种方法比第一种方法节省时间的原因是什么? 生:因为有组长在和老师同时打(板书同时打) 2.5分钟调整为4分钟 师:5分钟是用时做少的方案吗?咱们班有10个同学用时4分钟。 师:她分成了4组(2,2,2,1),用时4分钟,于是她得出了一条结论,你给大家读一读。 生:分的组越多,用时越少。 师:你同意她的观点吗?大家有没有也用时4分钟,但和她分组不一样的? 生:老师,我不同意,因为我分成了3组(3,3,1),也用时4分钟。 生介绍 师:分成4组用4分钟,分成这样的3组,也用时4分钟,看来并不是分的组越多,越省时间。 师:对比4分钟的分组方案和5分钟的分组方案,又节省时间的原因是什么?看看这组员数有什么特点? 师:后知道消息的人却通知了更多的人。前面的组长闲下来了,后面的组长还在干活。 3.3分钟 师:有没有比4分钟还省时的方案呢?咱们班有7个人特别会动脑筋,竟然用了3分钟,想不想听一听? (1)分步图 引导语言:第2分钟,谁和谁同时打给几个人?现在知道消息的有几个人?第3分钟,几个人同时打给几个人? 师:谁听明白了?再来说一说? (2)综合图 师:谁和他的想法一样,也来展示一下你的画法? 生介绍 师:大家比较一下(2,2,2,1)、(3,3,1)和3分钟的方法,第几分钟不一样?为什么可以4个人同时通知?所以省时的原因是什么呢? (板书:所有知道消息的人) (三)精讲 1、梳理画法(师配合板书) 师:第1分钟,工作人数?新接通知人数?1分钟后,知道消息总人数?知道消息学生人数? 师:第2分钟,工作人数?咱们可以先添枝再加叶,这样不会遗漏。新接通知人数?2分钟后,知道消息总人数?知道消息学生人数? 师:第3分钟,工作人数?还是先添枝再加叶,新接通知人数?3分钟后,知道消息总人数?知道消息学生人数? 师:在第3分钟时,还能否再多通知一个人?为什么? 2.学生练画 学生边说边画。 3.师:通知7人,需要3分钟,通知15人,最少需要多长时间呢?你怎么知道的?(配合板书) 4.发现规律 预设1:工作人数等于新接到通知的人数 预设2:知道消息的总人数是前一分钟的2倍。 师:为什么是2倍呢? 师:这些数字和“2”还有更进一步的缘分,1分钟后,知道消息的总人数是2人,2分钟后,知道消息的总人数是2*2,3分钟后,知道消息的总人数是2*2*2,4分钟后,知道消息的总人数是2*2*2*2,n分钟后,知道消息的总人数就是n个2相乘。 预设3:知道消息的学生人数比总人数少1。这1是谁? 预设4:知道消息的学生人数是乘2加1的规律。为什么? 根据规律继续跟随课件填表5到10分钟。 (四)演练 师:咱们学校有180人,最少花多长时间能通知到每个人呢?为什么? 师:要想使咱们的方案在现实生活中切实可行,还需要做些什么呢? (应事先设计好整个流程,知道谁通知谁,这样才能不重不漏) 师:按照这种方法,10分钟最多可以通知多少人? 师:从一开始只有老师1个人知道消息,到第10分钟就有了1024人知道,你现在有什么感觉? (五)总结拓展 1.优化思想总结 师:大家回忆我们原来学习的数学知识中,有没有如何节约时间的数学问题呢?(烙饼问题)怎样烙才最省时?(让锅都不空着)我们称为满锅优化(板书) 师:今天学习了《打电话》,怎样打最省时?我们称为满员优化(板书),这都是优化的数学思想。 2.倍增现象拓展 师:像这种成倍增长的问题,数学上还有一个著名的小故事,就是我们课前搜集的“棋盘上的麦粒学问”。 生介绍 师:这就是被爱因斯坦称为“第八大奇迹”的几何倍增学的来历。 师:在现实生活中,还有很多现象蕴含着 “倍增现象”,比如,细胞分裂,浮萍现象等,有兴趣的同学下课查阅一下这方面的资料。 五、板书设计 六、教学反思 1、课前完成预学单 在这个过程中,让每个孩子充分思考了,表达了,先经历一个自我优化的过程,可能优化后还不是最省时的,但很多孩子明白了省时的原因是什么。例如有的孩子说“有组长帮忙通知”,有的说“第一个方法是老师通知7个人,第二个方法是老师通知3个人,剩下的人同学通知”…,还有的说“通知的人数增加了”等等,说明孩子真的充分比较了自己的两种方法,经历了从低效到高效,从基本到优化。 2、课堂展示的更充分了 因为有了课前预学,我更清楚了孩子的认知水平,也更加清楚了谁和谁比,什么时候比,比的目的是什么。能够做到以学定教。所以课堂上分成三个层次选取了有代表性的方案展示,进而通过生生、师生之间的思辨进行比较找到最优方案。 3、规律的出示与板书相呼应 找规律环节没有借助表格,而是结合直观图示的讲解为规律作准备,因为规律本身就是和打电话用时最少的方案是相呼应的。 这样的调整就使学生对方案理解的更加透彻了。在画图中重点和孩子们强调了“先添枝后画页”的方法从而做到不重不漏。 两次课堂以来,我认为自己最大的变化是对教学目标的把握更准了,第一次课时,整节课节奏很快,7分钟1个人,4分钟展示1个人,对比,然后3分钟1个人,对比,得出方案,整个过程只是在为找最优方案而进行;而今天的过程,是让学生真的经历了这种逐步优化的过程,尊重学生的思维差异,通过充分的交流逐步经历探究的过程。 七、主持人点评 通过本次课堂实践效果来看,我更加坚定了两个做法: 1.提前设置预学。 兰老师针对“内容的丰富”与“时间的紧迫”这一矛盾,打破了传统教学方法,巧用预学单,因材施教,因情施教,关键处的点拨很到位,为师生们呈现了一节既新颖又扎实有效的数学活动课。在交流展示环节,兰老师充分尊重学生间的差异,循循善诱,通过有效的追问、灵动的引领,点燃了孩子们的求知欲。可以说,没有课堂上前半时的深入思考,就不会有后半时的高潮。 2.图表法解决问题的可行性。 “发现规律”的环节抛弃了只有枯燥数字的表格,而是采用了“先添枝后画叶”的直观图示法,水到渠成,为发现规律打好了根基、做好了铺垫,让课堂大放异彩。同时,此环节积极性最高,这得益于前面的充分展示和板书的合理运用。 同时,兰老师在课堂上能做到充分尊重学生,尊重孩子之间的认知差异,即使孩子们说不出来,兰老师也不急于让其他孩子替代说,而是耐心等待,合理引导。在课堂的最后,兰老师将“满锅优化”和“满员优化”做了知识间的沟通,将“倍增现象”渗透到了生活的其他领域,极大地激发了孩子们的求知欲望。 但是,面对时间的紧迫,展示环节应该有“简”有“舍”,当学生体会到“同时通知能够节省时间”时,教师可以再放手,让他们围绕着“同时”再次修改自己的方案,这样参与的积极性就会更高了。展示不是目的,而是要让学习真实的发生。查看更多