二年级上册数学教案 平移和旋转 北京版 (4)

二年级上册数学教案 平移和旋转 北京版 (4)

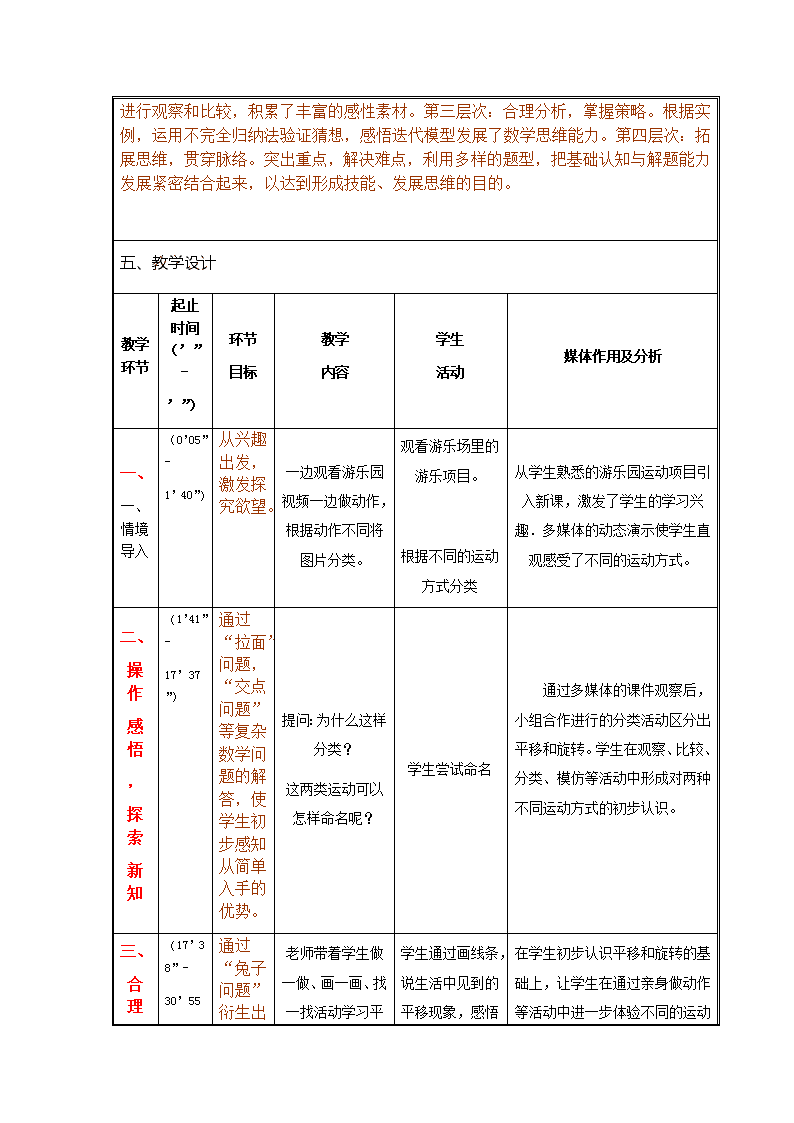
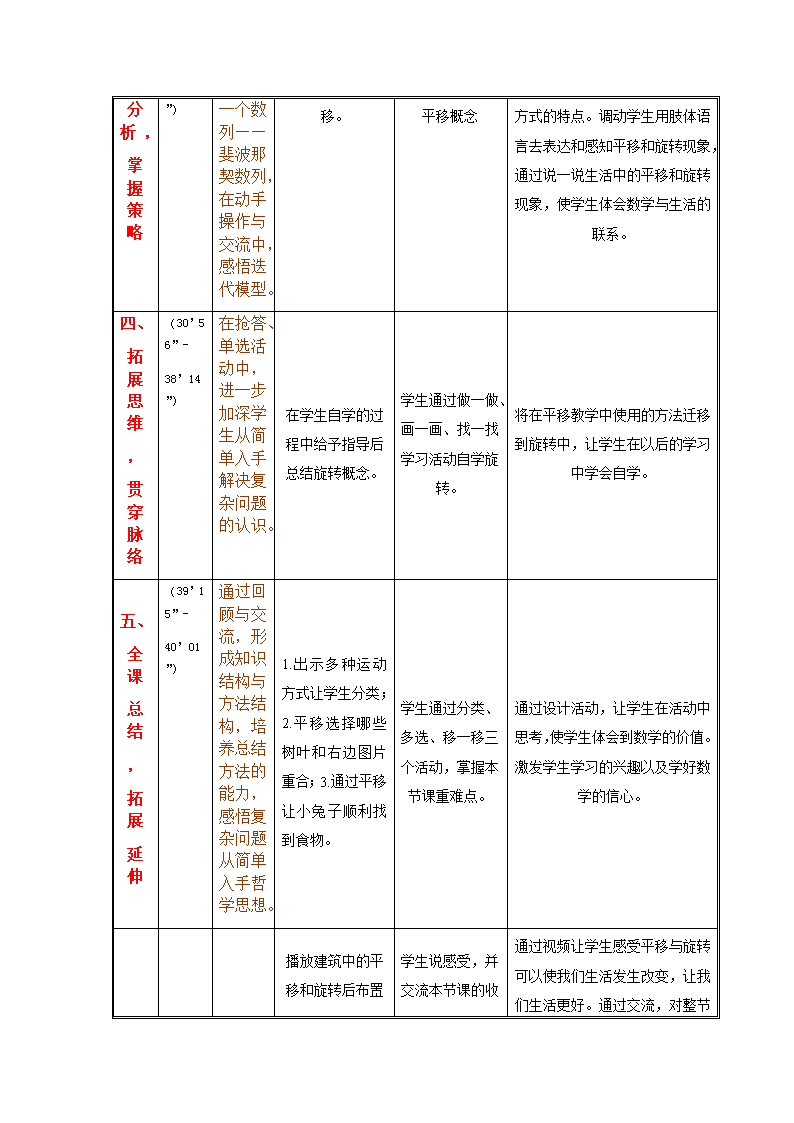
‎2019年新媒体新技术教学应用研讨会教学设计表 一、基本信息 学校 淮阴师范学院第一附属小学 课名 平移和旋转 教师姓名 学科（版本）‎ 小学数学（人教版）‎ 章节 学时 ‎1课时 年级 二年级 二、教学目标 ‎1. 学生通过观察现实生活中物体的运动，认识物体平移和旋转运动的特点；能区分、判断这两种不同的运动方式，能在平面图形上将物体按指定方向和距离（格数）平移。‎ ‎2. 学生经历观察、模拟、判断等活动过程，体会物体的运动，感受平移和旋转的不同方式，培养观察、判断等思维能力。‎ ‎3. 学生初步认识生活中的平移和旋转现象，感受数学与生活的密切联系；培养仔细观察、认真比较等意识。‎ 三、学习者分析 ‎1.学生在学习中对于遇到条件比较复杂，文字比较多，看起来很复杂的题目，往往不知道怎么去思考，无从下笔，没有先从简单情况思考的意识，长此以往学生遇到此类问题产生抵触情绪，消极对待生活与学习中的“难题”。‎ ‎2.解决问题的策略是小学数学的重要组成部分，学生以前已经学过列表法、枚举法，从问题（条件）思考等策略，这些都是本节课学生参与学习的能力基础。 ‎ ‎3.上课的学生全部都是城市孩子，他们都是伴随着新技术新产品成长起来的。平板、网络对于孩子们并不陌生；教室中的电子白板设备更是经常使用。这些现代化环境孕育了孩子们良好的信息技术素养。‎ 四、教学重难点分析及解决措施 教学重难点：学会从简单情况开始思考并且有步骤的解答“难题”。‎ 共分四个层次进行推进。第一层次：创设情境，激发兴趣。通过生活中熟知的视频，唤醒学生的已有生活经验，更好地做好教学的衔接，促进学生自觉实现知识迁移。第二层次：操作感悟，探索新知。让学生通过动手操作，研究具体的实例，并对数据进行观察和比较，积累了丰富的感性素材。第三层次：合理分析，掌握策略。根据实例，运用不完全归纳法验证猜想，感悟迭代模型发展了数学思维能力。第四层次：拓展思维，贯穿脉络。突出重点，解决难点，利用多样的题型，把基础认知与解题能力发展紧密结合起来，以达到形成技能、发展思维的目的。‎ 五、教学设计 教学环节 起止时间（’”-‎ ‎’”）‎ 环节 目标 教学 内容 学生 活动 媒体作用及分析 一、‎ 一、情境导入 ‎（0’05”-‎ ‎1’40”）‎ 从兴趣出发，激发探究欲望。‎ 一边观看游乐园视频一边做动作，根据动作不同将图片分类。‎ 观看游乐场里的游乐项目。‎ 根据不同的运动方式分类 从学生熟悉的游乐园运动项目引入新课，激发了学生的学习兴趣．多媒体的动态演示使学生直观感受了不同的运动方式。‎ 二、‎ 操作 感悟 ‎，‎ 探索 新知 ‎（1’41”-‎ ‎17’37”）‎ 通过“拉面”问题，“交点问题”等复杂数学问题的解答，使学生初步感知从简单入手的优势。‎ 提问：为什么这样分类？‎ 这两类运动可以怎样命名呢？‎ 学生尝试命名 通过多媒体的课件观察后，小组合作进行的分类活动区分出平移和旋转。学生在观察、比较、分类、模仿等活动中形成对两种不同运动方式的初步认识。‎ 三、‎ ‎（17’38”-‎ ‎30’55‎ 通过“兔子问题”‎ 合理分析 ，‎ 掌握策略 ‎”）‎ 衍生出一个数列——斐波那契数列，在动手操作与交流中，感悟迭代模型。‎ 老师带着学生做一做、画一画、找一找活动学习平移。‎ 学生通过画线条，说生活中见到的平移现象，感悟平移概念 在学生初步认识平移和旋转的基础上，让学生在通过亲身做动作等活动中进一步体验不同的运动方式的特点。调动学生用肢体语言去表达和感知平移和旋转现象，通过说一说生活中的平移和旋转现象，使学生体会数学与生活的联系。‎ 四、‎ 拓展思维 ‎，‎ 贯穿脉络 ‎（30’56”-‎ ‎38’14”）‎ 在抢答、单选活动中，进一步加深学生从简单入手解决复杂问题的认识。‎ 在学生自学的过程中给予指导后总结旋转概念。‎ 学生通过做一做、画一画、找一找学习活动自学旋转。‎ 将在平移教学中使用的方法迁移到旋转中，让学生在以后的学习中学会自学。‎ 五、‎ 全课 总结 ‎，‎ 拓展 延伸 ‎（39’15”-‎ ‎40’01”）‎ 通过回顾与交流，形成知识结构与方法结构，培养总结方法的能力，感悟复杂问题从简单入手哲学思想。‎ ‎1.出示多种运动方式让学生分类；2.平移选择哪些树叶和右边图片重合；3.通过平移让小兔子顺利找到食物。 ‎ 学生通过分类、多选、移一移三个活动，掌握本节课重难点。‎ 通过设计活动，让学生在活动中思考，使学生体会到数学的价值。激发学生学习的兴趣以及学好数学的信心。‎ 播放建筑中的平移和旋转后布置作业。‎ 学生说感受，并交流本节课的收获。‎ 通过视频让学生感受平移与旋转可以使我们生活发生改变，让我们生活更好。通过交流，对整节课的内容有了一个整体认识。‎ 板书设计 ‎……‎ 图示法 列举法 枚举法 面条问题 读题思考 ‎ ‎ 选择方法 交点问题 从简单入手 找出规律 兔子问题 解答检验