2011普陀区中考数学模拟试题

2011普陀区中考数学模拟试题

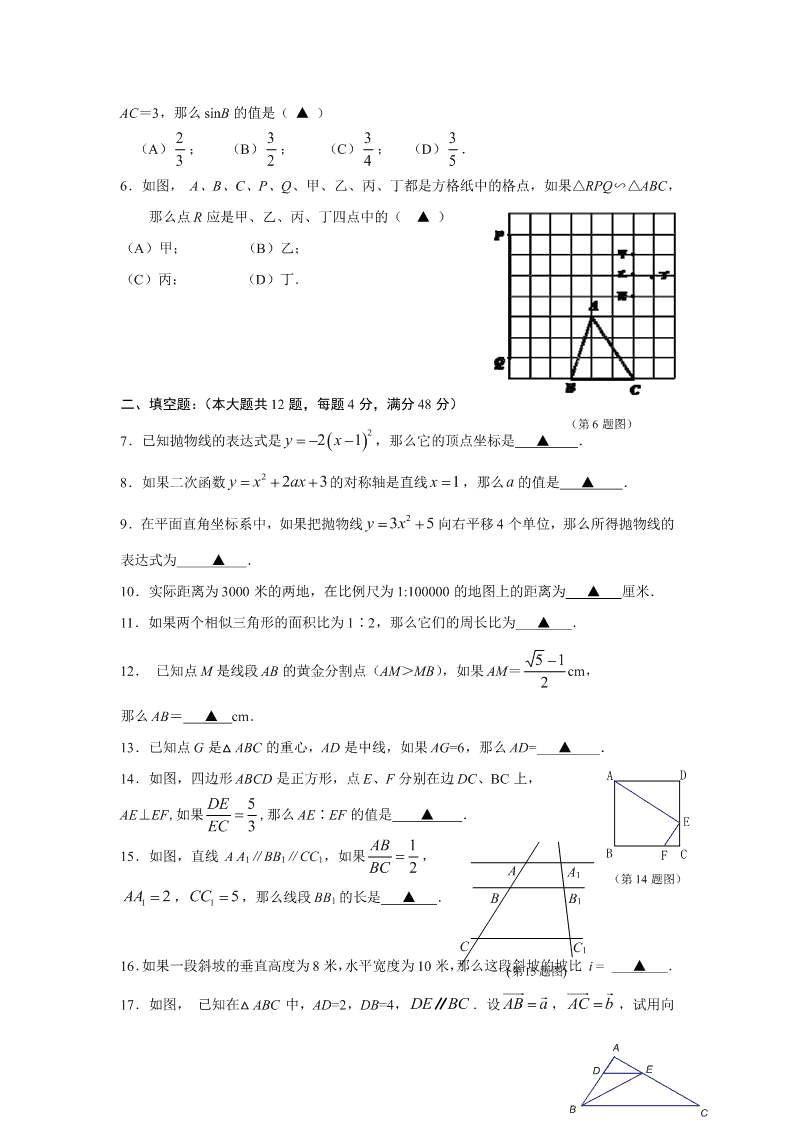
2011 年普陀区第一学期期末考试九年级数学试卷 （时间：100 分钟，满分：150 分） 考生注意： 1．本试卷含三个大题，共 25 题．答题时，考生务必按答题要求在答题纸规定的位置上作答， 在草稿纸、本试卷上答题一律无效． 2．除第一、二大题外，其余各题如无特别说明，都必须在答题纸的相应位置上写出证明或 计算的主要步骤． 一、单项选择题：（本大题共 6 题，每题 4 分，满分 24 分） [下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸 的相应位置上] 1．下列四个函数中，一定是二次函数的是（ ▲ ） （A） 2 1yxx； （B） 2y ax bx c   ； （C）  22 7y x x   ； （D） ( 1)(2 1)y x x   ． 2．下列说法中不正确．．．的是（ ▲ ） （A）如果 m 、 n 为实数，那么 m n a ma na   ； （B）如果 0k  或 0a  ，那么 0ka  ； （C）长度为 1 的向量叫做单位向量； （D）如果 为实数，那么 ()m a b ma mb   ． 3．已知二次函数 cbxaxy  2 的图像如图所示，那么 a、b、c 的符号为（ ▲ ） （A） a ＞0，b ＞0，c ＞0； （B） ＜0，b ＜0，c ＜0； （C） ＜0，b ＞0，c ＞0； （D） ＜0，b ＜0，c ＞0． 4．如图，能推得 DE∥BC 的条件是（ ▲ ） （A）AD∶AB=DE∶BC； （B）AD∶DB=DE∶BC； （C）AD∶DB=AE∶EC； （D）AE∶AC=AD∶DB． 5．如图，在 Rt△ABC 中，CD 是斜边 AB 上的中线，如果 CD＝2， （第 3 题图） O x y C A B D （第 5 题图） ED CB A （第 4 题图） AC＝3，那么 sinB 的值是（ ▲ ） （A） 2 3 ； （B） 3 2 ； （C） 3 4 ； （D） 3 5 ． 6．如图， A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点，如果△RPQ∽△ABC， 那么点 R 应是甲、乙、丙、丁四点中的（ ▲ ） （A）甲； （B）乙； （C）丙； （D）丁． 二、填空题：（本大题共 12 题，每题 4 分，满分 48 分） 7．已知抛物线的表达式是  221yx   ，那么它的顶点坐标是 ▲ ． 8．如果二次函数 2 23y x ax   的对称轴是直线 1x  ，那么 a 的值是 ▲ ． 9．在平面直角坐标系中，如果把抛物线 235yx向右平移 4 个单位，那么所得抛物线的 表达式为 ▲ ． 10．实际距离为 3000 米的两地，在比例尺为 1:100000 的地图上的距离为 ▲ 厘米． 11．如果两个相似三角形的面积比为 1∶2，那么它们的周长比为 ▲ ． 12． 已知点 M 是线段 AB 的黄金分割点（AM＞MB），如果 AM＝ 2 15  cm， 那么 AB＝ ▲ cm． 13．已知点 G 是△ ABC 的重心，AD 是中线，如果 AG=6，那么 AD= ▲ ． 14．如图，四边形 ABCD 是正方形，点 E、F 分别在边 DC、BC 上， AE⊥EF,如果 5 3 DE EC  ,那么 AE∶EF 的值是 ▲ ． 15．如图，直线 A A1∥BB1∥CC1，如果 1 2 AB BC  ， 1 2AA  ， 1 5CC  ，那么线段 BB1 的长是 ▲ ． 16．如果一段斜坡的垂直高度为 8 米，水平宽度为 10 米，那么这段斜坡的坡比 i = ▲ ． 17．如图， 已知在△ ABC 中，AD=2，DB=4， DE BC∥ ．设 AB a ， AC b ，试用向 （第 17 题图） ED CB A (第15题图) A B C A1 B1 C1 （第 6 题图） F E D CB A （第 14 题图） 量 a 、b 表示向量 BE = ▲ ． 18．已知在 ABC 中， 20AB  ， 12AC  ， 16BC  ，点 D 是射线 BC 上的一点（不与端点 B 重合），联结 AD，如果△ ACD 与△ ABC 相似， 那么 BD＝ ▲ ． 三、解答题：（本大题共 7 题，满分 78 分） 19．（本题满分 10 分） 计算：  02tan 60 cot 45 2011 cos60cos30 sin30         ． 20．（本题满分 10 分） 如图，已知两个不平行的向量a 、b ．先化简，再求作：2(a ＋ 1 2 b )－ 1 2 (2a －4b )． （不要求写作法，但要指出图中表示结论的向量） 21．（本题满分 10 分） 已知一个二次函数的图像经过  0,1A 、  1,3B 、  1,1C  三点， 求这个函数的解析式，并用配方法求出图像的顶点坐标． 22.（本题满分 10 分） 某学校体育场看台的侧面如图阴影部分所示，看台有四级高度相等的小台阶，每级小台 阶都为 0.4 米.现要做一个不锈钢的扶手 AB 及两根与 FG 垂直且长均为 l 米的不锈钢架杆 AD 和 BC（杆子的底端分别为 D，C），且 66DAB. （第 20 题图） a b 660 A B C G F H D 1 米 E （1）求点 D 与点 C 的高度差 DH 的长度； （2）求所用不锈钢材料的总长度l （即 AD＋AB＋BC， 结果精确到 0.1 米）. （参考数据：sin66 0.91 ， cos66 0.41 ， tan66 2.25 ， cot 66 0.45 ） 23．（本题满分 12 分） 如图，在 ABC△ 中， 90BAC，AD 是 BC 边上的高，点 E 在线段 DC 上，EF AB ， EG AC ，垂足分别为 FG， ．求证： （1） EG CG AD CD ； （2） FD ⊥ DG ． 24. （本题满分 12 分） 如图，已知 为直角三角形， 90ACB， AC BC ，点 A、C 在 x 轴上，点 B 坐标为（3，m）(m＞0)，线段 AB 与 y 轴相交于点 D，以 P（1，0）为顶点的二次函数图像 经过点 B、D． （1）用 m 表示点 A、D 的坐标； （2）求这个二次函数的解析式； G F ED CB A （第 23 题图） （第 24 题图） y x D O P C B A （3）点 Q 为二次函数图像上点 P 至点 B 之间的一点， 且点 Q 到 ABC△ 边 BC 、 AC 的距离相等，联结 PQ、BQ， 求四边形 ABQP 的面积． 25、（本题满分 14 分） 在 ABC△ 中， 90ACB， 4AC  , 3BC  ，D 是边 AC 上一动点（不与端点 A 、C 重合），过动点 的直线 l 与射线 AB 相交于点 E ，与射线 BC 相交于点 F， （1）设 1CD  ，点 在边 上， ADE△ 与 相似，求此时 BE 的长度． （2）如果点 E 在边 AB 上，以点 E、B、F 为顶点的三角形与以点 E、A、D 为顶点的三角 形相似，设 CD＝x， BF＝y，求 y 与 x 之间的函数解析式并写出函数的定义域． （3）设 ，以点 E、B、F 为顶点的三角形与以点 E、A、D 为顶点的三角形相似， A B C A B C 求 :△ △EBF EADSS的值．