2009年山东省济宁市中考数学试卷(全解全析)

2009年山东省济宁市中考数学试卷(全解全析)

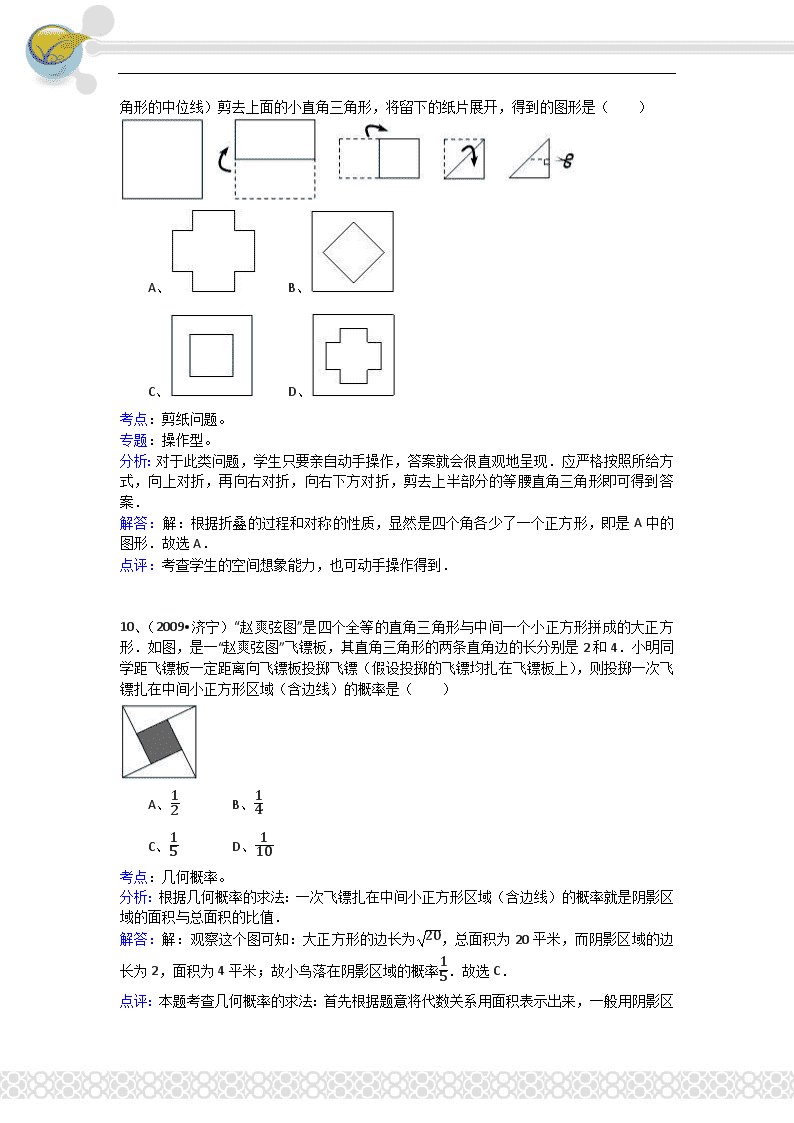
点评：正确理解负整数指数次幂的含义，幂的乘方，积的乘方的运算法则是解答此题的关键．‎ ‎4、（2009•济宁）山东省地矿部门经过地面磁测，估算济宁磁异常铁矿的内蕴经济资源量为10 800 000 000吨．这个数据用科学记数法表示为（　　）‎ ‎ A、108×108吨 B、10.8×109吨 ‎ C、1.08×1010吨 D、1.08×1011吨 考点：科学记数法—表示较大的数；估算无理数的大小。‎ 专题：应用题。‎ 分析：由于把一个数M记成a×10n（1≤|a|＜10，n为整数）的形式，这种记数的方法叫做科学记数法，其中确定a×10n（1≤|a|＜10，n为整数）中n的值是易错点，由于10 800 000 000有11位，所以可以确定n=11﹣1=10．‎ 解答：解：10 800 000 000=1.08×1010吨．‎ 故选C．‎ 点评：此题主要考查了利用科学记数法解决实际问题，把一个数M记成a×10n（1≤|a|＜10，n为整数）的形式，这种记数的方法叫做科学记数法．规律：‎ ‎（1）当|a|≥1时，n的值为a的整数位数减1；‎ ‎（2）当|a|＜1时，n的值是第一个不是0的数字前0的个数，包括整数位上的0．‎ ‎5、（2009•牡丹江）下列图形中，既是中心对称图形又是轴对称图形的是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：中心对称图形；轴对称图形；生活中的旋转现象。‎ 分析：根据轴对称图形与中心对称图形的概念和图形特点求解．‎ 解答：解：A、D：都只是轴对称图形；‎ B：只是中心对称图形；‎ C：既是轴对称图形，也是中心对称图形．‎ 故选C．‎ 点评：掌握好中心对称图形与轴对称图形的概念．同时要注意，轴对称图形的关键是寻找对称轴，两部分折叠后可重合．中心对称图形是要寻找对称中心，图形旋转180度后与原图重合．‎ ‎6、（2010•常州）在函数y=‎‎1‎x﹣3‎中，自变量x的取值范围是（　　）‎ ‎ A、x≠3 B、x≠0‎ ‎ C、x＞3 D、x≠﹣3‎ 考点：函数自变量的取值范围；分式有意义的条件。‎ 专题：计算题。‎ 分析：求函数自变量的取值范围，就是求函数解析式有意义的条件，分式有意义的条件是：分母不等于0．‎ 解答：解：根据题意得：x﹣3≠0‎ 解得：x≠3；‎ 故选A．‎ 点评：当函数表达式是分式时，函数要有意义，则要使分式的分母不能为0．‎ ‎7、（2009•济宁）如图，在长为8cm、宽为4cm的矩形中，截去一个矩形，使得留下的矩形（图中阴影部分）与原矩形相似，则留下矩形的面积是（　　）‎ ‎ A、2cm2 B、4cm2‎ ‎ C、8cm2 D、16cm2‎ 考点：相似多边形的性质。‎ 分析：利用相似多边形的对应边的比相等，对应角相等分析．‎ 解答：解：长为8cm、宽为4cm的矩形的面积是32cm2，‎ 留下的矩形（图中阴影部分）与原矩形相似，‎ 相似比是4：8=1：2，‎ 因而面积的比是1：4，‎ 因而留下矩形的面积是32×‎1‎‎4‎=8cm2．‎ 故选C．‎ 点评：本题考查相似多边形的性质．相似多边形面积之比等于相似比的平方．‎ ‎8、（2009•济宁）已知a为实数，那么‎﹣‎a‎2‎等于（　　）‎ ‎ A、a B、﹣a ‎ C、﹣1 D、0‎ 考点：二次根式的性质与化简。‎ 分析：根据非负数的性质，只有a=0时，‎﹣‎a‎2‎有意义，可求根式的值．‎ 解答：解：根据非负数的性质a2≥0，根据二次根式的意义，﹣a2≥0，‎ 故只有a=0时，‎﹣‎a‎2‎有意义，‎ 所以，‎﹣‎a‎2‎=0．故选D．‎ 点评：注意：平方数和算术平方根都是非负数，这是解答此题的关键．‎ ‎9、（2009•‎ 济宁）将一正方形纸片按下列顺序折叠，然后将最后折叠的纸片沿虚线（直角三角形的中位线）剪去上面的小直角三角形，将留下的纸片展开，得到的图形是（　　）‎ ‎ A、 B、‎ ‎ C、 D、‎ 考点：剪纸问题。‎ 专题：操作型。‎ 分析：对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．应严格按照所给方式，向上对折，再向右对折，向右下方对折，剪去上半部分的等腰直角三角形即可得到答案．‎ 解答：解：根据折叠的过程和对称的性质，显然是四个角各少了一个正方形，即是A中的图形．故选A．‎ 点评：考查学生的空间想象能力，也可动手操作得到．‎ ‎10、（2009•济宁）“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形．如图，是一“赵爽弦图”飞镖板，其直角三角形的两条直角边的长分别是2和4．小明同学距飞镖板一定距离向飞镖板投掷飞镖（假设投掷的飞镖均扎在飞镖板上），则投掷一次飞镖扎在中间小正方形区域（含边线）的概率是（　　）‎ ‎ A、‎1‎‎2‎ B、‎‎1‎‎4‎ ‎ C、‎1‎‎5‎ D、‎‎1‎‎10‎ 考点：几何概率。‎ 分析：根据几何概率的求法：一次飞镖扎在中间小正方形区域（含边线）的概率就是阴影区域的面积与总面积的比值．‎ 解答：解：观察这个图可知：大正方形的边长为‎20‎，总面积为20平米，而阴影区域的边长为2，面积为4平米；故小鸟落在阴影区域的概率‎1‎‎5‎．故选C．‎ 点评：‎ 本题考查几何概率的求法：首先根据题意将代数关系用面积表示出来，一般用阴影区域表示所求事件（A）；然后计算阴影区域的面积在总面积中占的比例，这个比例即事件（A）发生的概率；关键是得到两个正方形的边长．‎ ‎11、（2009•济宁）一个几何体的三视图如图所示，那么这个几何体的侧面积是（　　）‎ ‎ A、4π B、6π ‎ C、8π D、12π 考点：由三视图判断几何体。‎ 分析：根据三视图正视图以及左视图都为矩形，底面是圆形，则可想象出这是一个圆柱体．侧面积=底面周长×高．‎ 解答：解：∵圆柱的直径为2，高为3，∴侧面积为2×‎1‎‎2‎×2×3π=6π．故选B．‎ 点评：本题难点是确定几何体的形状，关键是找到等量关系里相应的量．‎ ‎12、（2009•济宁）小强从如图所示的二次函数y=ax2+bx+c的图象中，观察得出了下面五条信息：（1）a＜0；（2）c＞1；（3）b＞0；（4）a+b+c＞0；（5）a﹣b+c＞0．你认为其中正确信息的个数有（　　）‎ ‎ A、2个 B、3个 ‎ C、4个 D、5个 考点：二次函数图象与系数的关系。‎ 分析：由抛物线的开口方向判断a与0的关系，由抛物线与y轴的交点判断c与0的关系，然后根据对称轴及抛物线与x轴交点情况进行推理，进而对所得结论进行判断．‎ 解答：解：（1）由抛物线的开口向下知a＜0，故正确；‎ ‎（2）由抛物线与y轴的交点为在y轴的正半轴上且大于1，可推出c＞1，故正确；‎ ‎（3）由图可知对称轴为x=‎﹣‎b‎2a＞0，可推出a、b异号，又∵a＜0，∴b＞0，故正确；‎ ‎（4）因为抛物线与x轴的交点可以看出，当x=1时，y＞0，所以a+b+c＞0，故正确，‎ ‎（5）因为抛物线与x轴的交点可以看出，当x=﹣1时，y＜0，所以a﹣b+c＜0，错误．‎ ‎∴正确答案为4个．‎ 故选C．‎ 点评：二次函数y=ax2+bx+c系数符号的确定物线开口方向、对称轴和抛物线与y轴的交点确定．‎ 二、填空题（共6小题，每小题3分，满分18分）‎ ‎13、（2009•济宁）分解因式：ax2﹣a= ．‎ 考点：提公因式法与公式法的综合运用。‎ 分析：应先提取公因式a，再利用平方差公式进行二次分解．‎ 解答：解：ax2﹣a，‎ ‎=a（x2﹣1），‎ ‎=a（x+1）（x﹣1）．‎ 点评：主要考查提公因式法分解因式和利用平方差公式分解因式，分解因式要彻底，直到不能再分解为止．‎ ‎14、（2009•济宁）已知两圆的半径分别是2和3，圆心距为6，那么这两圆的位置关系是 ．‎ 考点：圆与圆的位置关系。‎ 分析：先计算两圆半径的和与差，再与圆心距比较，即可得出两圆的位置关系．‎ 解答：解：因为R+r=5＜6，根据圆心距大于两圆半径的和可知，两圆外离．‎ 点评：本题主要考查两圆的位置关系．两圆的位置关系有：相离（d＞R+r）、相切（外切：d=R+r或内切：d=R﹣r）、相交（R﹣r＜d＜R+r）．‎ ‎15、（2009•济宁）在等腰梯形ABCD中，AD∥BC，AD=3cm，AB=4cm，∠B=60°，则下底BC的长为 cm．‎ 考点：等腰梯形的性质。‎ 分析：解决此题的关键是作等腰梯形的两条高，再通过中间的平行四边形转化边的关系，利用直角三角形求出BE的长，然后就可求出下底的长．‎ 解答：解：如图所示，分别过A，D点作高AE，DF ‎∵在RT△ABE中，AB=4cm，∠B=60°‎ ‎∴BE=2cm ‎∵△ABE≌△DCF ‎∴BE=CF ‎∵AD∥BC，AE，DF分别是两条高 ‎∴AD=EF ‎∴BC=2BE+AD=4+3=7cm 点评：此题考查了学生对等腰梯形的性质及三角函数的掌握情况．‎ ‎16、（2009•济宁）如图，⊙A和⊙B都与x轴和y轴相切，圆心A和圆心B都在反比例函数y=‎1‎x的图象上，则图中阴影部分的面积等于 （结果保留π）．‎ 考点：反比例函数图象的对称性。‎ 专题：计算题。‎ 分析：根据两函数的对称性和圆的对称性，将阴影部分面积转化为一个圆的面积来解．‎ 解答：解：由题意得，图中阴影部分的面积即为一个圆的面积．‎ ‎⊙A和x轴y轴相切，‎ 因而A到两轴的距离相等，即横纵坐标相等，‎ 设A的坐标是（a，a），‎ 点A在函数y=‎1‎x的图象上，因而a=1．‎ 故阴影部分的面积等于π．‎ 故答案为：π．‎ 点评：能够观察到阴影部分的面积是圆面积，是解决本题的关键．‎ ‎17、（2009•济宁）请你阅读下面的诗句：“栖树一群鸦，鸦树不知数，三只栖一树，五只没去处，五只栖一树，闲了一棵树，请你仔细数，鸦树各几何”诗句中谈到的鸦为 只，树为 棵．‎ 考点：二元一次方程组的应用。‎ 专题：阅读型。‎ 分析：通过理解题意可知本题存在两个等量关系，即3×树的棵树+5=鸦的只数，5×（树的棵树﹣1）=鸦的只数，根据这两个等量关系可列出方程组．‎ 解答：解：可设鸦有x只，树y棵．‎ 则‎&3y+5=x‎&5（y﹣1）=x，解得‎&x=20‎‎&y=5‎．‎ 答：鸦有20只，树有5棵．‎ 点评：解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系，列出方程组，再求解．‎ ‎18、（2009•济宁）观察图中每一个大三角形中白色三角形的排列规律，则第5‎ 个大三角形中白色三角形有 个．‎ 考点：规律型：图形的变化类。‎ 专题：规律型。‎ 分析：解决此题关键在观察、分析已知数据，寻找它们之间的以及与第一个图形的相互联系，探寻其规律．‎ 解答：解：第1个大三角形中白色三角形有1个；第2个大三角形中白色三角形有（1+3）个；第3个大三角形中白色三角形有（1+3+32）个；那么第5个大三角形中白色三角形有（1+3+32+33+34）=121个．‎ 点评：此类题型是规律性问题．注意由特殊到一般的分析方法，此题的规律为（1+3+32+…+3n﹣1）．‎ 三、解答题（共8小题，满分66分）‎ ‎19、（2009•济宁）计算：（π﹣1）0+‎（‎‎1‎‎2‎‎）‎‎﹣1‎+‎∣5﹣‎27‎∣‎﹣2‎‎3‎ 考点：实数的运算；零指数幂；负整数指数幂；二次根式的性质与化简。‎ 分析：按照实数的运算法则依次计算；‎ 考查知识点：负指数幂、0指数幂、绝对值、二次根式的化简．‎ 解答：解：原式=1+2+（‎27‎﹣5）﹣2‎‎3‎ ‎=3+3‎3‎﹣5﹣2‎‎3‎ ‎=‎3‎﹣2．‎ 点评：传统的小杂烩计算题．涉及知识：负指数为正指数的倒数；任何非0数的0次幂等于1；绝对值的化简；二次根式的化简．‎ ‎20、（2010•遵义）解方程：‎x﹣3‎x﹣2‎‎+1=‎‎3‎‎2﹣x 考点：解分式方程。‎ 专题：计算题。‎ 分析：观察可得2﹣x=﹣（x﹣2），所以可确定方程最简公分母为：（x﹣2），然后去分母将分式方程化成整式方程求解．注意检验．‎ 解答：解：方程两边同乘以（x﹣2），‎ 得：x﹣3+（x﹣2）=﹣3，‎ 解得x=1，‎ 检验：x=1时，x﹣2≠0，‎ ‎∴x=1是原分式方程的解．‎ 点评：（1）解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．‎ ‎（2）解分式方程一定注意要验根．‎ ‎（3）去分母时有常数项的不要漏乘常数项．‎ ‎21、（2009•济宁）作为一项惠农强农应对当前国际金融危机、拉动国内消费需求的重要措施，“家电下乡”工作已经国务院批准从2008年12月1日起在我市实施．我市某家电公司营销点自去年12月份至今年5月份销售两种不同品牌冰箱的数量如下图：‎ ‎（1）完成下表：‎ ‎（2）请你依据折线图的变化趋势，对营销点今后的进货情况提出建议．‎ 考点：算术平均数；折线统计图；方差。‎ 专题：图表型。‎ 分析：（1）读图可得数据，故甲品牌的方差为‎1‎‎6‎（9+4+1+1+9）=‎13‎‎3‎；乙品牌的平均数为‎1‎‎6‎（9+10+11+9+11+10）=10；‎ ‎（2）根据折线图，分析可得建议，答案不唯一．‎ 解答：解：（1）计算平均数、方差如下表：‎ ‎（2）建议如下：从折线图来看，甲品牌冰箱的月销售量呈上升趋势，进货时可多进甲品牌冰箱．‎ 点评：本题考查平均数、方差的计算，及根据折线图分析数据，解决问题的能力．‎ ‎22、（2009•济宁）坐落在山东省汶上县宝相寺内的太子灵踪塔始建于北宋（公元1112年），为砖彻八角形十三层楼阁式建筑．数学活动小组开展课外实践活动，在一个阳光明媚的上午，他们去测量太子灵踪塔的高度，携带的测量工具有：测角仪、皮尺、小镜子．‎ ‎（1）小华利用测角仪和皮尺测量塔高．图1为小华测量塔高的示意图．她先在塔前的平地上选择一点A，用测角仪测出看塔顶（M）的仰角α=35°，在A点和塔之间选择一点B，测出看塔顶（M）的仰角β=45°，然后用皮尺量出A、B两点的距离为18.6m，自身的高度为1.6m．请你利用上述数据帮助小华计算出塔的高度；（tan35°≈0.7，结果保留整数）‎ ‎（2）如果你是活动小组的一员，正准备测量塔高，而此时塔影NP的长为am（如图2），你能否利用这一数据设计一个测量方案如果能，请回答下列问题：‎ ‎①在你设计的测量方案中，选用的测量工具是： ；‎ ‎②要计算出塔的高，你还需要测量哪些数据 ．‎ 考点：解直角三角形的应用-仰角俯角问题。‎ 专题：阅读型；方案型。‎ 分析：（1）根据题意构造直角三角形，利用其公共边构造方程求解．‎ ‎（2）根据题目中的情景，结合解三角形的知识设计测量方法．‎ 解答：解：（1）设CD的延长线交MN于E点，MN长为x，‎ 则ME=x﹣1.6．‎ ‎∵β=45°，‎ ‎∴DE=ME=x﹣1.6．‎ ‎∴CE=x﹣1.6+18.6=x+17．‎ ‎∵MECE=tanα=tan35°，‎ ‎∴x﹣1.6‎x+17‎‎=0.7‎，‎ 解得x=45．‎ ‎∴太子灵踪塔（MN）的高度为45m．‎ ‎（2）①测角仪、皮尺；‎ ‎②站在P点看塔顶的仰角、自身的高度．‎ 点评：本题考查仰角的应用：要求学生借助仰角关系构造直角三角形，并结合图形解三角形或设计测量方法．‎ ‎23、（2009•济宁）阅读下面的材料：在平面几何中，我们学过两条直线平行的定义．下面就两个一次函数的图象所确定的两条直线，给出它们平行的定义：设一次函数y=k1x+b1（k1≠0）的图象为直线l1，一次函数y=k2x+b2（k2≠0）的图象为直线l2，若k1=k2，且b1≠b2，我们就称直线l1与直线l2互相平行．解答下面的问题：‎ ‎（1）求过点P（1，4）且与已知直线y=﹣2x﹣1平行的直线l的函数表达式，并画出直线l的图象；‎ ‎（2）设直线l分别与y轴、x轴交于点A、B，如果直线m：y=kx+t（t＞0）与直线l平行且交x轴于点C，求出△ABC的面积S关于t的函数表达式．‎ 考点：一次函数综合题。‎ 专题：阅读型；新定义；开放型。‎ 分析：（1）直线l与已知直线y=﹣2x﹣1平行，因而直线的一次项系数是﹣2，根据待定系数法就可以求出函数解析式．‎ ‎（2）点A、B的坐标可以求出，点C的位置应分在B点的左侧和右侧两种情况进行讨论．根据三角形的面积就可以求出C点的坐标．‎ 解答：解：（1）设直线l的函数表达式为y=kx+b，‎ ‎∵直线l与直线y=﹣2x﹣1平行，∴k=﹣2，‎ ‎∵直线l过点（1，4），‎ ‎∴﹣2+b=4，‎ ‎∴b=6．‎ ‎∴直线l的函数表达式为y=﹣2x+6．‎ 直线l的图象如图．‎ ‎（2）∵直线l分别与y轴、x轴交于点A、B，∴点A、B的坐标分别为（0，6）、（3，0）．‎ ‎∵l∥m，∴直线m为y=﹣2x+t．‎ ‎∴C点的坐标为（t‎2‎，0）．‎ ‎∵t＞0，∴t‎2‎＞0．‎ ‎∴C点在x轴的正半轴上．‎ 当C点在B点的左侧时，S=‎1‎‎2‎×（3﹣t‎2‎）×6=9﹣‎3t‎2‎；‎ 当C点在B点的右侧时，S=‎1‎‎2‎×（t‎2‎﹣3）×6=‎3t‎2‎﹣9．‎ ‎∴△ABC的面积S关于t的函数表达式为S=‎&9﹣‎3t‎2‎（0＜t＜6）‎‎&‎3t‎2‎﹣9（t＞6）‎．（8分）‎ 点评：本题主要考查了待定系数法求函数的解析式，以及函数平行的条件，是需要熟记的内容．‎ ‎24、（2009•济宁）如图，△ABC中，∠C=90°，AC=4，BC=3．半径为1的圆的圆心P以1个单位/s的速度由点A沿AC方向在AC上移动，设移动时间为t（单位：s）．‎ ‎（1）当t为何值时，⊙P与AB相切；‎ ‎（2）作PD⊥AC交AB于点D，如果⊙P和线段BC交于点E，证明：当t=‎16‎‎5‎s时，四边形PDBE为平行四边形．‎ 考点：切线的性质；平行四边形的判定；相似三角形的判定与性质。‎ 专题：综合题。‎ 分析：（1）当⊙P在移动中与AB相切时，设切点为M，连接PM，根据△APM∽△ABC可求得t的值；‎ ‎（2）由BC⊥AC，PD⊥AC，易得BC∥DP，再分别求得PD、BE的值，证明其相等，即可得出四边形PDBE为平行四边形的结论．‎ 解答：解：（1）当⊙P在移动中与AB相切时，‎ 设切点为M，连接PM，则∠AMP=90°，‎ ‎∴△APM∽△ABC，‎ ‎∴APAB‎=‎PMBC，‎ ‎∵AP=t，AB=AC‎2‎+BC‎2‎‎=5‎，‎ ‎∴t‎5‎‎=‎‎1‎‎3‎，‎ ‎∴t=‎‎5‎‎3‎．（4分）‎ ‎（2）证明：∵BC⊥AC，PD⊥AC，‎ ‎∴BC∥DP，‎ 当t=‎16‎‎5‎s时，AP=‎16‎‎5‎，‎ ‎∴PC=4﹣‎16‎‎5‎‎=‎‎4‎‎5‎，‎ ‎∴EC=‎PE‎2‎﹣PC‎2‎‎=‎1‎‎2‎‎﹣‎‎（‎4‎‎5‎）‎‎2‎=‎‎3‎‎5‎ ‎∴BE=BC﹣EC=3﹣‎3‎‎5‎‎=‎‎12‎‎5‎，‎ ‎∵△ADP∽△ABC，‎ ‎∴PDBC‎=‎APAC，‎ ‎∴PD‎3‎‎=‎‎16‎‎5‎‎4‎，‎ ‎∴PD=‎12‎‎5‎，‎ ‎∴PD=BE，‎ ‎∴当t=‎16‎‎5‎s时，四边形PDBE为平行四边形．（9分）‎ 点评：此题主要考查切线的性质、相似三角形的判定和性质以及平行四边形的判定．‎ ‎25、（2009•济宁）某体育用品商店购进一批滑板，每件进价为100元，售价为130元，每星期可卖出80件．商家决定降价促销，根据市场调查，每降价5元，每星期可多卖出20件．‎ ‎（1）求商家降价前每星期的销售利润为多少元？‎ ‎（2）降价后，商家要使每星期的销售利润最大，应将售价定为多少元？最大销售利润是多少？‎ 考点：二次函数的应用。‎ 分析：（1）已知原每天利润为130﹣100，每星期可卖出80件，则（130﹣100）×80=2400元．‎ ‎（2）设将售价定为x元，则销售利润为y=（x﹣100）（80+‎130﹣x‎5‎×20）=﹣4（x﹣125）2+2500，故可求出y的最大值．‎ 解答：解：‎ ‎（1）（130﹣100）×80=2400（元）；（4分）‎ ‎∴商家降价前每星期的销售利润为2400元 ‎（2）设应将售价定为x元，‎ 则销售利润y=（x﹣100）（80+‎130﹣x‎5‎×20）（6分）‎ ‎=﹣4x2+1000x﹣60000=﹣4（x﹣125）2+2500．（8分）‎ 当x=125时，y有最大值2500．‎ ‎∴应将售价定为125元，最大销售利润是2500元．（9分）‎ 点评：本题考查的是二次函数的应用．求二次函数的最大（小）值有三种方法，第一种可由图象直接得出，第二种是配方法，第三种是公式法．‎ ‎26、（2009•济宁）在平面直角坐标中，边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上，点O在原点．现将正方形OABC绕O点顺时针旋转，当A点第一次落在直线y=x上时停止旋转，旋转过程中，AB边交直线y=x于点M，BC边交x轴于点N（如图）．‎ ‎（1）求边OA在旋转过程中所扫过的面积；‎ ‎（2）旋转过程中，当MN和AC平行时，求正方形OABC旋转的度数；‎ ‎（3）设△MBN的周长为p，在旋转正方形OABC的过程中，p值是否有变化？请证明你的结论．‎ 考点：坐标与图形变化-旋转；全等三角形的判定；正方形的性质；扇形面积的计算。‎ 专题：综合题；压轴题。‎ 分析：（1）根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积；‎ ‎（2）解决本题需利用全等，根据正方形一个内角的度数求出∠AOM的度数；‎ ‎（3）利用全等把△MBN的各边整理到成与正方形的边长有关的式子．‎ 解答：解：（1）∵A点第一次落在直线y=x上时停止旋转，‎ ‎∴OA旋转了45度．‎ ‎∴OA在旋转过程中所扫过的面积为‎45π×‎‎2‎‎2‎‎360‎‎=‎π‎2‎．‎ ‎（2）∵MN∥AC，‎ ‎∴∠BMN=∠BAC=45°，∠BNM=∠BCA=45度．‎ ‎∴∠BMN=∠BNM．∴BM=BN．‎ 又∵BA=BC，∴AM=CN．‎ 又∵OA=OC，∠OAM=∠OCN，∴△OAM ≌△OCN．‎ ‎∴∠AOM=∠CON．∴∠AOM=‎1‎‎2‎（90°﹣45°）=22.5度．‎ ‎∴旋转过程中，当MN和AC平行时，正方形OABC旋转的度数为45°﹣22.5°=22.5度．‎ ‎（3）证明：延长BA交y轴于E点，则∠AOE=45°﹣∠AOM，∠CON=90°﹣45°﹣∠AOM=45°﹣∠AOM，‎ ‎∴∠AOE=∠CON．‎ 又∵OA=OC，∠OAE=180°﹣90°=90°=∠OCN．‎ ‎∴△OAE ≌△OCN．‎ ‎∴OE=ON，AE=CN．‎ 又∵∠MOE=∠MON=45°，OM=OM，‎ ‎∴△OME ≌△OMN．∴MN=ME=AM+AE．‎ ‎∴MN=AM+CN，‎ ‎∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4．‎ ‎∴在旋转正方形OABC的过程中，p值无变化．‎ 点评：本题用到的知识点是：扇形面积=nπr‎2‎‎360‎，求一些线段的长度或角的度数，总要整理到已知线段的长度上或已知角的度数上．‎ 参与本试卷答题和审题的老师有：‎ wdxwzk；lanchong；wangcen；lf2-9；HJJ；zcx；hnaylzhyk；lzhzkkxx；hbxglhl；张长洪；zhjh；开心；huangling；zhangCF；cook2360；MMCH；kaixinyike；zhehe；yu123；lanyan；csiya；mmll852；CJX；ln_86；wdxwwzy；workeroflaw；xinruozai；137-hui；lanyuemeng。（排名不分先后）‎ ‎2011年2月19日