2009中考数学分类汇编-二次函数与一元二次方程

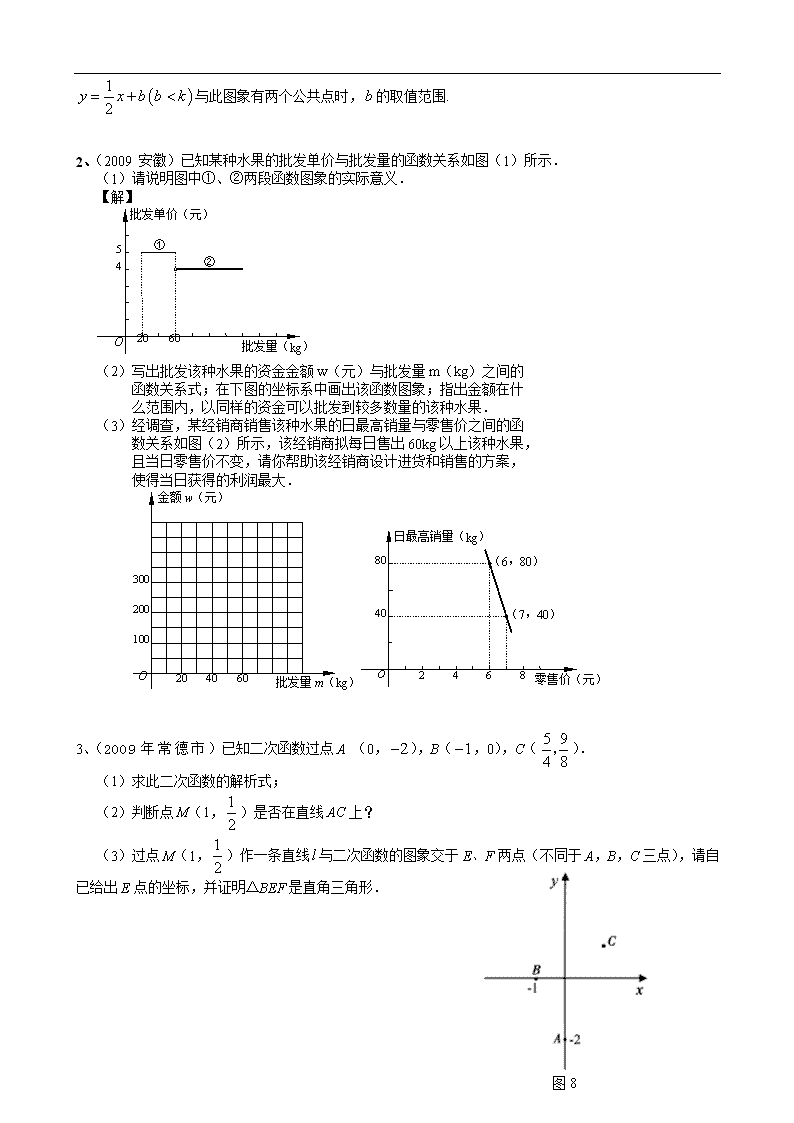
2009中考数学分类汇编-二次函数与一元二次方程

一、选择题 ‎1、（2009年台湾）下列哪一个函数，其图形与x轴有两个交点？‎ ‎ (A) y=17(x+83)2+2274 (B) y=17(x-83)2+2274 (C) y= -17(x-83)2-2274‎ ‎ (D) y= -17(x+83)2+2274。‎ ‎2、（2009年台州市）已知二次函数的与的部分对应值如下表：‎ ‎…‎ ‎0‎ ‎1‎ ‎3‎ ‎…‎ ‎…‎ ‎1‎ ‎3‎ ‎1‎ ‎…‎ 则下列判断中正确的是（　 　）‎ A．抛物线开口向上　　　　　　 B．抛物线与轴交于负半轴 C．当＝4时，＞0 D．方程的正根在3与4之间 二、填空题 ‎1、（2009年内蒙古包头）将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值是 cm2．‎ ‎2、（2009年甘肃白银）抛物线的部分图象如图8所示，请写出与其关系式、图象相关的2个正确结论：　　　　　　　　　，　　　　　　　　　　．（对称轴方程，图象与x正半轴、y轴交点坐标例外）‎ ‎3、（2009年甘肃庆阳）从地面垂直向上抛出一小球，小球的高度h（米）与小球运动时间t（秒）的函数关系式是，那么小球运动中的最大高度为 米．‎ ‎ ‎ ‎4、（2009年包头）将一条长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形，则这两个正方形面积之和的最小值 是 cm2． ‎ ‎5、（2009年包头）已知二次函数的图象与轴交于点、，且，与轴的正半轴的交点在的下方．下列结论：①；②；③；④．其中正确结论的个数是 个．‎ 三、解答题 ‎1、（2009年北京市）已知关于的一元二次方程有实数根，为正整数.‎ ‎（1）求的值；‎ ‎（2）当此方程有两个非零的整数根时，将关于的二次函数的图象向下平移8个单位，求平移后的图象的解析式；‎ ‎（3）在（2）的条件下，将平移后的二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线 与此图象有两个公共点时，的取值范围. ‎ ‎2、（2009 安徽）已知某种水果的批发单价与批发量的函数关系如图（1）所示．‎ ‎（1）请说明图中①、②两段函数图象的实际意义．‎ ‎【解】‎ O ‎60‎ ‎20‎ ‎4‎ 批发单价（元）‎ ‎5‎ 批发量（kg）‎ ‎①‎ ‎②‎ ‎（2）写出批发该种水果的资金金额w（元）与批发量m（kg）之间的 函数关系式；在下图的坐标系中画出该函数图象；指出金额在什 么范围内，以同样的资金可以批发到较多数量的该种水果．‎ ‎（3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函 数关系如图（2）所示，该经销商拟每日售出60kg以上该种水果，‎ 且当日零售价不变，请你帮助该经销商设计进货和销售的方案，‎ 使得当日获得的利润最大．‎ 金额w（元）‎ O 批发量m（kg）‎ ‎300‎ ‎200‎ ‎100‎ ‎20‎ ‎40‎ ‎60‎ O ‎6‎ ‎2‎ ‎40‎ 日最高销量（kg）‎ ‎80‎ 零售价（元）‎ ‎4‎ ‎8‎ ‎（6，80）‎ ‎（7，40）‎ ‎3、（2009年常德市）已知二次函数过点A （0，），B（，0），C（）．‎ ‎ （1）求此二次函数的解析式；‎ ‎ （2）判断点M（1，）是否在直线AC上？‎ 图8‎ ‎ （3）过点M（1，）作一条直线与二次函数的图象交于E、F两点（不同于A，B，C三点），请自已给出E点的坐标，并证明△BEF是直角三角形．‎ ‎4、（2009年湖南长沙）为了扶持大学生自主创业，市政府提供了80万元无息贷款，用于某大学生开办公司生产并销售自主研发的一种电子产品，并约定用该公司经营的利润逐步偿还无息贷款．已知该产品的生产成本为每件40元，员工每人每月的工资为2500元，公司每月需支付其它费用15万元．该产品每月销售量（万件）与销售单价（元）之间的函数关系如图所示．‎ ‎（1）求月销售量（万件）与销售单价（元）之间的函数关系式；‎ ‎（2）当销售单价定为50元时，为保证公司月利润达到5万元（利润＝销售额－生产成本－员工工资－其它费用），该公司可安排员工多少人？‎ ‎（3）若该公司有80名员工，则该公司最早可在几个月后还清无息贷款？‎ ‎4‎ ‎2‎ ‎1‎ ‎40‎ ‎60‎ ‎80‎ x ‎（元）‎ ‎（万件）‎ y ‎5、（2009年内蒙古包头）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．‎ ‎（1）求一次函数的表达式；‎ ‎（2）若该商场获得利润为元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？‎ ‎（3）若该商场获得利润不低于500元，试确定销售单价的范围．‎ ‎6、（2009年杭州市）已知平行于x轴的直线与函数和函数的图象分别交于点A和点B，又有定点P（2，0）．‎ ‎（1）若，且tan∠POB=，求线段AB的长；‎ ‎（2）在过A，B两点且顶点在直线上的抛物线中，已知线段AB=，且在它的对称轴左边时，y随着x的增大而增大，试求出满足条件的抛物线的解析式；‎ O ‎1‎ ‎1‎ P(2，0)‎ x y ‎（第24题）‎ ‎（3）已知经过A，B，P三点的抛物线，平移后能得到 的图象，求点P到直线AB的距离．‎ ‎7、（2009年娄底）已知关于x的二次函数y=x2-（‎2m-1）x+m2+‎3m+4. ‎（1）探究m满足什么条件时，二次函数y的图象与x轴的交点的个数. ‎（2）设二次函数y的图象与x轴的交点为A（x1，0），B（x2，0），且+=5，与y轴的交点为C，它的顶点为M，求直线CM的解析式.‎ ‎9、（2009烟台市）某商场将进价为2000元的冰箱以2400元售出，平均每天能售出8台，为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰箱的售价每降低50元，平均每天就能多售出4台．‎ ‎ （1）假设每台冰箱降价x元，商场每天销售这种冰箱的利润是y元，请写出y与x之间的函数表达式；（不要求写自变量的取值范围）‎ ‎ （2）商场要想在这种冰箱销售中每天盈利4800元，同时又要使百姓得到实惠，每台冰箱应降价多少元？‎ ‎ （3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？‎ ‎10、（2009年孝感）已知抛物线（k为常数，且k＞0）．‎ ‎（1）证明：此抛物线与x轴总有两个交点；‎ ‎（2）设抛物线与x轴交于M、N两点，若这两点到原点的距离分别为OM、ON，且，求k的值．‎ ‎11、（2009年新疆）（1）用配方法把二次函数变成的形成．‎ ‎（2）在直角坐标系中画出的图象．‎ ‎（3）若是函数图象上的两点，且，请比较的大小关系．（直接写结果）‎ ‎（4）把方程的根在函数的图象上表示出来．‎ ‎【‎ ‎12、（2009年天津市）已知函数为方程的两个根，点在函数的图象上．‎ ‎（Ⅰ）若，求函数的解析式；‎ ‎（Ⅱ）在（Ⅰ）的条件下，若函数与的图象的两个交点为，当的面积为时，求的值；‎ ‎（Ⅲ）若，当时，试确定三者之间的大小关系，并说明理由．‎ ‎12、（2009年广西梧州）如图（9）-1，抛物线经过A（，0），C（3，）两点，与轴交于点D，与轴交于另一点B．‎ ‎（1）求此抛物线的解析式；‎ ‎（2）若直线将四边形ABCD面积二等分，求的值；‎ ‎（3）如图（9）-2，过点E（1，1）作EF⊥轴于点F，将△AEF绕平面内某点旋转180°得△MNQ（点M、N、Q分别与点A、E、F对应），使点M、N在抛物线上，作MG⊥轴于点G，若线段MG︰AG＝1︰2，求点M，N的坐标．‎ E F M N G O B A x y 图（9）-2‎ Q D O B A x y C y=kx+1‎ 图（9）-1‎ ‎13、2009年包头）某商场试销一种成本为每件60元的服装，规定试销期间销售单价不低于成本单价，且获利不得高于45%，经试销发现，销售量（件）与销售单价（元）符合一次函数，且时，；时，．‎ ‎（1）求一次函数的表达式；‎ ‎（2）若该商场获得利润为元，试写出利润与销售单价之间的关系式；销售单价定为多少元时，商场可获得最大利润，最大利润是多少元？‎ ‎（3）若该商场获得利润不低于500元，试确定销售单价的范围．‎ ‎14、（2009年北京市）已知关于的一元二次方程有实数根，为正整数.‎ ‎（1）求的值；‎ ‎（2）当此方程有两个非零的整数根时，将关于的二次函数的图象向下平移8个单位，求平移后的图象的解析式；‎ ‎（3）在（2）的条件下，将平移后的二次函数的图象在轴下方的部分沿轴翻折，图象的其余部分保持不变，得到一个新的图象.请你结合这个新的图象回答：当直线 与此图象有两个公共点时，的取值范围. ‎ ‎15、（09湖南怀化）如图11，已知二次函数的图象与轴相交于两个不同的点、，与轴的交点为．设的外接圆的圆心为点．‎ ‎（1）求与轴的另一个交点D的坐标；‎ ‎（2）如果恰好为的直径，且的面积等于，求和的值． ‎ ‎16、(2009年达州)如图11，抛物线与轴相交于A、B两点（点A在点B右侧），过点A的直线交抛物线于另一点C，点C的坐标为（-2，6）.‎ ‎(1)求a的值及直线AC的函数关系式；‎ ‎(2)P是线段AC上一动点，过点P作y轴的平行线，交抛物线于点M，交x轴于点N.‎ ‎①求线段PM长度的最大值；‎ ‎②在抛物线上是否存在这样的点M，使得△CMP与△APN相似？如果存在，请直接写出所有满足条件的点M的坐标（不必写解答过程）；如果不存在，请说明理由. ‎ ‎17、（2009年邵阳市）如图（十二）直线l的解析式为y＝－x+4,　它与x轴、y轴分相交于A、B两点，平行于直线l的直线m从原点O出发，沿x轴的正方向以每秒1个单位长度的速度运动，它与x轴、y轴分别相交于M、N两点，运动时间为t秒（0

查看更多