2012年山东省威海市中考数学试题（含答案）

2012年山东省威海市中考数学试题（含答案）

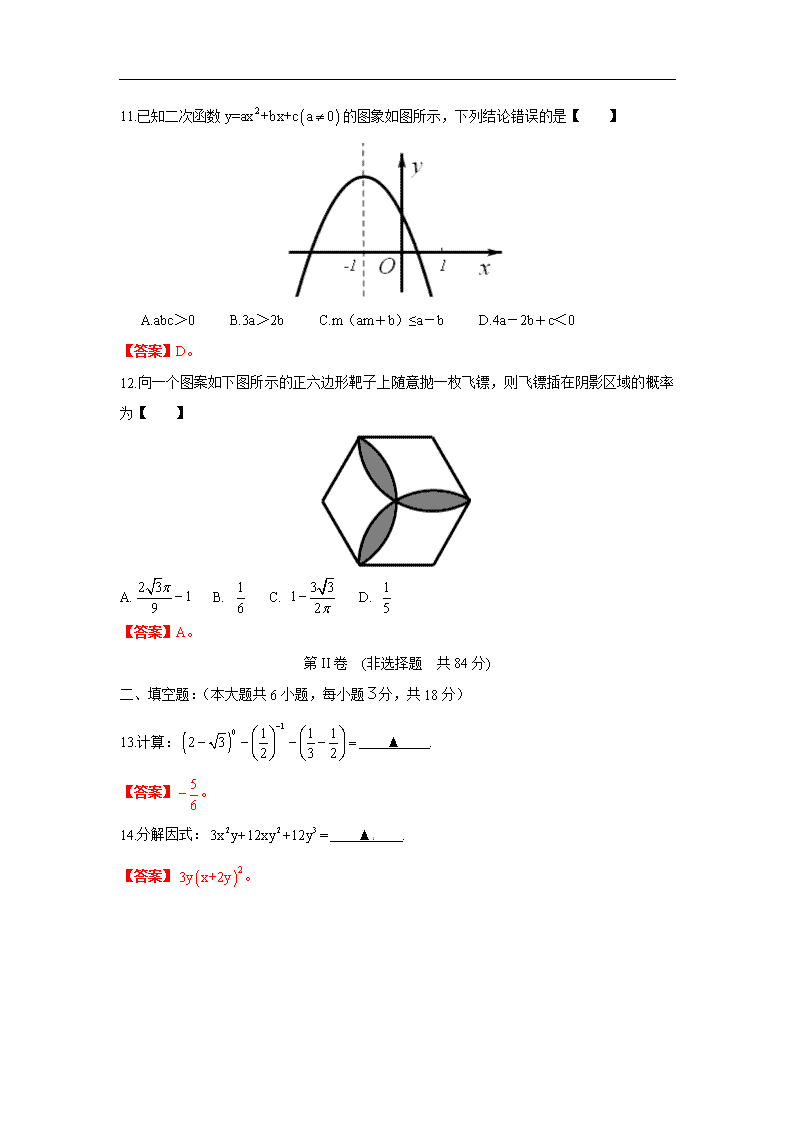
‎2012年中考数学试题（山东威海卷）‎ ‎（本试卷满分120分，考试时间120分钟）‎ 第Ⅰ卷 (选择题 共36分)‎ 一、选择题：（本大题共12小题，每小题３分，共36分）‎ ‎1. 64的立方根是【 】‎ A.8 B.±8 C.4 D.±4‎ ‎【答案】C。‎ ‎2. 2012年是威海市实施校安工程4年规划的收官年。截止4月底，全市已开工项目39个，投入资金4999万元。请将4999万用科学计数法表示【 】（保留两个有效数字）‎ A.4999×104 B. 4.999×107 C. 4.9×107 D. 5.0×107‎ ‎【答案】D。‎ ‎3.如图，a∥b，点A在直线a上，点C在直线b上，∠BAC=900，AB=AC。若∠1=200，则∠2的度数为【 】‎ ‎ A.250 B.650 C.700 D.750‎ ‎【答案】B。‎ ‎4.下列运算正确的是【 】‎ A. B. C. D. ‎ ‎【答案】C。‎ ‎5.如图所示的零件的左视图是【 】‎ ‎【答案】C。‎ ‎6.函数的自变量x的取值范围是【 】‎ A. x＞3 B. x≥3 C. x≠3 D. x＜－3‎ ‎【答案】A。[来源:学#科#网Z#X#X#K]‎ ‎7.某外贸公司要出口一批食品罐头，标准质量为每听454克，现抽取10听样品进行检测，它们的质量与标准质量的差值（单位：克）如下：‎ ‎ －10，＋5，0，＋5，0，0，－5，0，＋5，＋10。‎ 则这10听罐头质量的平均数及众数为【 】‎ A.454，454 B.455，454 C.454，459 D.455，0‎ ‎【答案】B。‎ ‎8.化简的结果是【 】‎ A. B. C. D. ‎ ‎【答案】B。‎ ‎9.下列选项中，阴影部分面积最小的是【 】‎ ‎【答案】C。‎ ‎10.如图，在ABCD中，AE，CF分别是∠BAD和∠BCD的平分线。添加一个条件，仍无法判断四边形AECF为菱形的是【 】‎ A.AE=AF B.EF⊥AC C.∠B=600 D.AC是∠EAF的平分线 ‎【答案】C。‎ ‎11.已知二次函数的图象如图所示，下列结论错误的是【 】‎ A.abc＞0 B.3a＞2b C.m（am＋b）≤a－b D.4a－2b＋c＜0‎ ‎【答案】D。‎ ‎12.向一个图案如下图所示的正六边形靶子上随意抛一枚飞镖，则飞镖插在阴影区域的概率为【 】‎ A. B. C. D. ‎ ‎【答案】A。‎ 第II卷 (非选择题 共84分)‎ 二、填空题：（本大题共6小题，每小题３分，共18分）‎ ‎13.计算： ▲ .‎ ‎【答案】。‎ ‎14.分解因式： ▲ .‎ ‎【答案】。[来源:Zxxk.Com]‎ ‎15.如图，直线l1，l2交于点A。观察图象，点A的坐标可以看作方程组 ▲ 的解.‎ ‎【答案】。‎ ‎16.若关于x的方程的两根互为倒数，则a= ▲ .【答案】－1。‎ ‎17.如图，在平面直角坐标系中，△ABC的顶点坐标分别为（4，0）（8，2），（6，4）。已知△A1B1C1的两个顶点的坐标为（1，3），（2，5）。若△ABC与△A1B1C1位似，则△A1B1C1的第三个顶点的坐标为 ▲ .‎ ‎【答案】（3，4）或（0，4）。‎ ‎18.如图，在平面直角坐标系中，线段OA1=1，OA1与x轴的夹角为300。线段A1A2=1，A1A2⊥OA1，垂足为A1；线段A2A3=1，A2A3⊥A1A2，垂足为A2；线段A3A4=1，A3A4⊥A2A3，垂足为A3；···按此规律，点A2012的坐标为 ▲ .‎ ‎【答案】。‎ 三、解答题：（本大题共7小题，共66分）‎ ‎19.解不等式组，并把解集表示在数轴上：‎ ‎【答案】解：解不等式①，得x≤－2，‎ ‎ 解不等式②，得x＞－3。‎ ‎ ∴原不等式组的解为－3＜x≤－2。‎ ‎ 原不等式组的解在数轴上表示为：‎ ‎20.如图，AB为⊙的直径，弦CD⊥AB，垂为点E。K为上一动点，AK、DC的延长线相交于点F，连接CK、KD。‎ ‎（1）求证：∠AKD=∠CKF；‎ ‎（2）若，AB=10，CD=6，求tan∠CKF的值。‎ ‎【答案】解：（1）证明：连接AD。‎ ‎ ∵∠CKF是圆内接四边形ADCK的外角，‎ ‎ ∴∠CKF=∠ADC。‎ ‎ ∵AB为⊙的直径，弦CD⊥AB，∴。‎ ‎ ∴∠ADC=∠AKD。∴∠AKD =∠CKF。‎ ‎（2）连接OD。‎ ‎ ∵AB为⊙的直径，AB=10，∴OD=5。‎ ‎ ∵弦CD⊥AB，CD=6，∴DE=3。‎ ‎ 在Rt△ODC中，。∴AE=9。‎ ‎ 在Rt△ADE中，。‎ ‎ ∵∠CKF=∠ADE，∴。‎ ‎21.某市为提高学生参与体育活动的积极性，2011年9月围绕“你喜欢的体育运动项目（只写一篇）”这一问题，对初一新生进行随机抽样调查。下面是根据调查结果绘制成的统计图（不完整），‎ 请你根据图中提供的信息解答下列问题：‎ ‎（1）本次抽样调查的样本容量是多少？‎ ‎（2）根据条形统计图中的数据，求扇形条形统计图中“最喜欢足球运动”的学生数对应扇形的圆心角度数。‎ ‎（3）请将条形统计图补充完整。‎ ‎（4）若该市2011年约有初一新生21000人，请我估计全市本届学生中“最喜欢足球运动”的学生约有多少人？‎ ‎【答案】解：（1）∵100÷20%=500，‎ ‎ ∴本次抽样调查的样本容量是500。‎ ‎ （2）∵，‎ ‎ ∴扇形条形统计图中“最喜欢足球运动”的学生数对应扇形的圆心角度数为43.20。‎ ‎ （3）补充条形统计图如下：‎ ‎ （4）∵（人），‎ ‎ ∴估计全市本届学生中“最喜欢足球运动”的学生约有2520人。‎ ‎22.小明计划用360元从大型系列科普丛书《什么是什么》（每本价格相同）中选购部分图书。“六一”期间，书店推出优惠政策：该系列丛书8折销售。这样，小明比原计划多买了6本。求每本书的原价和小明实际购买图书的数量。‎ ‎【答案】解：设每本书的原价为x元，则实际价格为0.8 x元，根据题意，得 ‎ 。‎ ‎ 解得，x=15。‎ ‎ 经检验，x=15是所列方程的根。‎ ‎ ∴（本）。‎ ‎ ∴每本书的原价为15元，小明实际购买图书30本。‎ ‎23. ‎ ‎（1）如图①，ABCD的对角线AC、BD交于点O。直线EF过点O，分别交AD、BC于点E、F ‎ 求证：AE=CF。‎ ‎（2）如图②，将ABCD（纸片）沿过对角线交点O的直线EF折叠，点A落在点A1处，点B落在点B1处。设FB1交CD于点G，A1B1分别交CD、DE于点H、I。‎ ‎ 求证：EI=FG。‎ ‎[来源:学科网ZXXK]‎ ‎【答案】证明：（1）∵四边形ABCD是平行四边形，∴AD∥BC。∴∠EAO=∠FCO，∠AEO=∠CFO。‎ ‎ 又∵四边形ABCD是平行四边形，∴OA=OC。‎ ‎ ∴△AOE≌△COF（AAS）。∴AE=CF。‎ ‎ （2）由（1）得，AE=CF。‎ ‎ ∵由折叠性质，得AE=A1E，∴A1E=CF。‎ ‎ ∵∠A1=∠A=∠C，∠B1=∠B=∠D，‎ ‎ ∴∠EIA1=∠DIH=1800－∠D－∠DHI=1800－∠B1－∠B1HG=∠B1GH=∠FGC。‎ ‎ 在△EIA1和△FGC中，∵∠A1=∠C，∠EIA1 =∠FGC，A1E=CF，‎ ‎ ∴△EIA1≌△FGC（AAS）。∴EI=FG。‎ ‎24. ‎ 探索发现：已知：在梯形ABCD中，CD∥AB，AD、BC的延长线相交于点E，AC、BD相交于点O，连接EO并延长交AB于点M，交CD于点N。‎ ‎（1）如图①，如果AD=BC，求证：直线EM是线段AB的垂直平分线；‎ ‎（2）如图②，如果AD≠BC，那么线段AM与BM是否相等？请说明理由。‎ 学以致用：仅用直尺（没有刻度），试作出图③中的矩形ABCD的一条对称轴。（写出作图步骤，保留作图痕迹）‎ ‎【答案】解：（1）证明：∵AD=BC，CD∥AB，∴AC=BD，∠DAB=∠CBA。∴AE=BE。‎ ‎ ∴点E在线段AB的垂直平分线上。‎ ‎ 在△ABD和△BAC中，∵AB=BA，AD=BC，AC=BD，‎ ‎ ∴△ABD≌△BAC（SSS）。∴∠DBA=∠CAB。∴OA=OB。‎ ‎ ∴点O在线段AB的垂直平分线上。[来源:学|科|网Z|X|X|K]‎ ‎ ∴直线EM是线段AB的垂直平分线。‎ ‎（2）相等。理由如下：‎ ‎ ∵CD∥AB，∴△EDN∽△EAM，△ENC∽△EMB，△EDC∽△EAB。‎ ‎∴。∴。∴。‎ ‎ ∵CD∥AB，∴△OND∽△OMB，△ONC∽△OMA，△OCD∽△OAB。‎ ‎∴。∴。∴。‎ ‎ ∴。∴AM2=BM2。∴AM=BM。‎ ‎（3）作图如下：‎ ‎ 作法：① 连接AC，BD，两线相交于点O1；‎ ‎ ② 在梯形ABCD外DC上方任取一点E，连接EA，EB，分别交DC于点G，H；‎ ‎ ③ 连接BG，AH，两线相交于点O2； ‎ ‎④ 作直线EO2，交AB于点M；‎ ‎⑤ 作直线MO1。‎ 则直线MO1。就是矩形ABCD的一条对称轴。‎ ‎25.如图，在平面直角坐标系中，抛物线的顶点为B（2，1），且过点A（0，2）。直线与抛物线交于点D、E（点E在对称轴的右侧）。抛物线的对称轴交直线于点C，交x轴于点G。PM⊥x轴，垂足为点F。点P在抛物线上，且位于对称轴的右侧，PM⊥x轴，垂足为点M，△PCM为等边三角形。‎ ‎ （1）求该抛物线的表达式；‎ ‎ （2）求点P的坐标；‎ ‎ （3）试判断CE与EF是否相等，并说明理由；‎ ‎（4）连接PE，在x轴上点M的右侧是否存在一点N，使△CMN与△CPE全等？若存在，试求出点N 的坐标；若不存在，请说明理由。‎ ‎【答案】解：（1）∵抛物线的顶点为B（2，1），‎ ‎ ∴可设抛物线的解析式为。‎ ‎ 将A（0，2）代入，得，解得。‎ ‎ ∴该抛物线的表达式。‎ ‎（2）将代入，得，‎ ‎ ∴点C的坐标为（2，2），即CG=2。‎ ‎ ∵△PCM为等边三角形，∴∠CMP=600，CM=PM。‎ ‎ ∵PM⊥x轴，，∴∠CMG=300。∴CM=4，GM=。∴OM=，PM=4。‎ ‎ ∴点P的坐标为（，4）。[来源:Z|xx|k.Com]‎ （3） 相等。理由如下：‎ 联立和得，解得，。‎ ‎ ∵不合题意，舍去，‎ ‎∴EF=，点E的坐标为（，）。‎ ‎ ∴。‎ ‎ 又∵，∴。‎ ‎ ∴CE=EF。‎ （4） 不存在。理由如下：‎ 假设在x轴上点M的右侧存在一点N，使△CMN≌△CPE，则CN=CE，∠MCN=∠PCE。‎ ‎ ∵∠MCP=600，∴∠NCE=600。‎ ‎∴△CNE是等边三角形。‎ ‎∴EN=CE，∠CEN=600。‎ 又∵由（3）CE=EF，∴EN=EF。‎ 又∵点E是直线上的点，∴∠CEF=450。‎ ‎∴点N与点F不重合。‎ ‎∵EF⊥x轴，这与“垂线段最短”矛盾，∴原假设错误，满足条件的点N不存在。‎