中考数学第一轮复习导学案函数综合应用

中考数学第一轮复习导学案函数综合应用

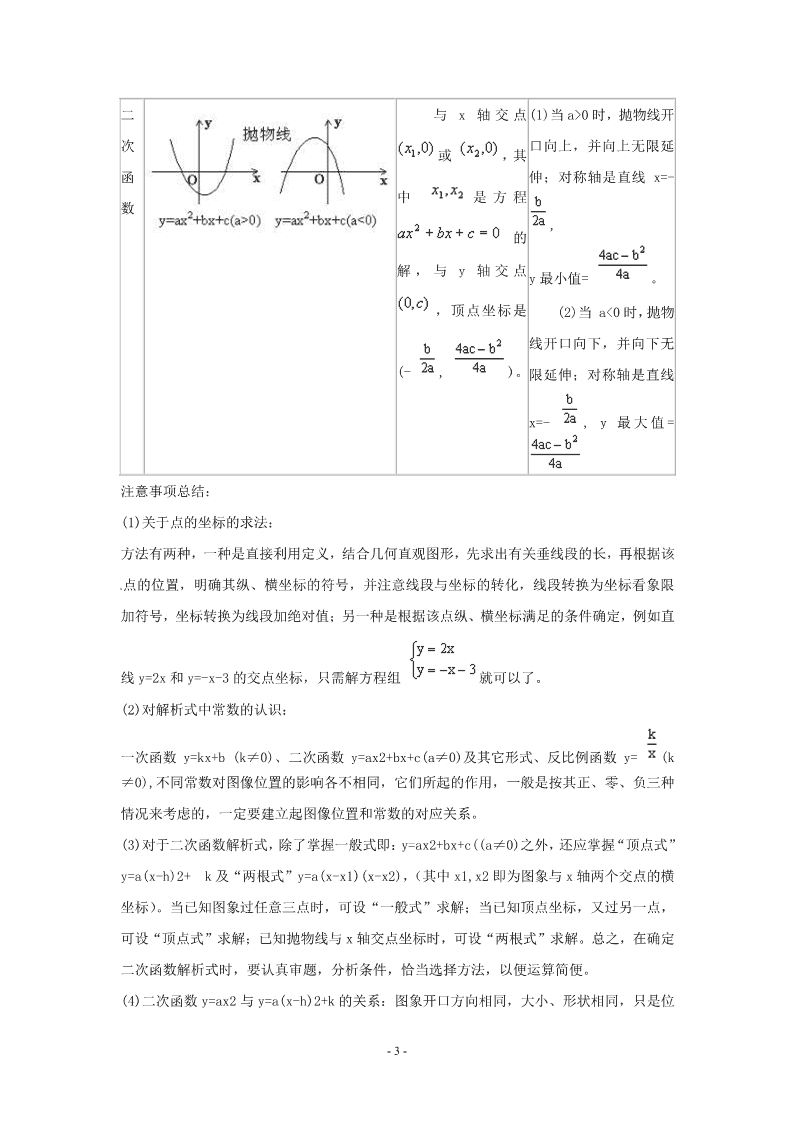
- 1 - 函数的综合应用 ◆ 课前热身 1．已知 y 关于 x 的函数图象如图所示，则当 0y  时，自变量 x 的取值范围是（ ） A． 0x  B． 11x   或 2x  C． 1x  D． 1x  或12x 2．在平面直角坐标系中，函数 1yx   的图象经过（ ） A．一、二、三象限 B．二、三、四象限 C．一、三、四象限 D．一、二、四象限 3.点 (13)P ， 在反比例函数 ky x （ 0k  ）的图象上，则 k 的值是（ ）． A． 1 3 B．3 C． 1 3 D． 3 4、如图为二次函数 2y ax bxc   的图象，给出下列说法： ① 0ab  ；②方程 2 0axbxc的根为 1213xx ， ；③ 0abc；④当 1x  时， y 随 x 值的增大而增大；⑤当 0y  时， 13x  ． 其中，正确的说法有 ．（请写出所有正确说法的序号） 【参考答案】 1. B 2. D 3. B 4.①②④ ◆考点聚焦 知识点 一次函数与反比例函数的综合应用；一次函数与二次函数的综合应用；二次函数与图象信息 1 O y x 1 2 - 2 - 类有关的实际应用问题 大纲要求 灵活运用函数解决实际问题 考查重点及常考题型 利用函数解决实际问题，常出现在解答题中 ◆备考兵法 1.四种常见函数的图象和性质总结 图象 特殊点 性质 一 次 函 数 与 x 轴交点 与 y 轴交点（0，b） (1)当 k>0 时，y 随 x 的增大而增大；(2)当 k<0 时，y 随 x 的增大而 减小. 正 比 例 函 数 与 x、y 轴交点是 原点(0,0)。 (1)当 k>0 时，y 随 x 的增大而增大，且直线 经过第一、三象限； (2)当 k<0 时，y 随 x 的增大而减小，且直线 经过第二、四象限 反 比 例 函 数 与坐标轴没有交 点，但与坐标轴无限 靠近。 (1)当 k>0 时，双曲 线经过第一、三象限， 在每个象限内，y 随 x 的 增大而减小； (2) 当 k<0 时，双 曲线经过第二、四象限， 在每个象限内，y 随 x 的 增大而增大。 - 3 - 二 次 函 数 与 x 轴 交 点 或 ，其 中 是 方 程 的 解，与 y 轴 交 点 ，顶点坐标是 (- , )。 (1)当 a>0 时，抛物线开 口向上，并向上无限延 伸；对称轴是直线 x=- , y 最小值= 。 (2)当 a<0 时，抛物 线开口向下，并向下无 限延伸；对称轴是直线 x=- , y 最大值= 注意事项总结： (1)关于点的坐标的求法： 方法有两种，一种是直接利用定义，结合几何直观图形，先求出有关垂线段的长，再根据该 点的位置，明确其纵、横坐标的符号，并注意线段与坐标的转化，线段转换为坐标看象限 加符号，坐标转换为线段加绝对值；另一种是根据该点纵、横坐标满足的条件确定，例如直 线 y=2x 和 y=-x-3 的交点坐标，只需解方程组 就可以了。 (2)对解析式中常数的认识： 一次函数 y=kx+b (k≠0)、二次函数 y=ax2+bx+c(a≠0)及其它形式、反比例函数 y= (k ≠0),不同常数对图像位置的影响各不相同，它们所起的作用，一般是按其正、零、负三种 情况来考虑的，一定要建立起图像位置和常数的对应关系。 (3)对于二次函数解析式，除了掌握一般式即：y=ax2+bx+c((a≠0)之外，还应掌握“顶点式” y=a(x-h)2+ k 及“两根式”y=a(x-x1)(x-x2)，（其中 x1,x2 即为图象与 x 轴两个交点的横 坐标）。当已知图象过任意三点时，可设“一般式”求解；当已知顶点坐标，又过另一点， 可设“顶点式”求解；已知抛物线与 x 轴交点坐标时，可设“两根式”求解。总之，在确定 二次函数解析式时，要认真审题，分析条件，恰当选择方法，以便运算简便。 (4)二次函数 y=ax2 与 y=a(x-h)2+k 的关系：图象开口方向相同，大小、形状相同，只是位 - 4 - 置不同。y=a(x-h)2+k 图象可通过 y=ax2 平行移动得到。当 h>0 时，向右平行移动|h|个单 位；h<0 向左平行移动|h|个单位；k>0 向上移动|k|个单位；k<0 向下移动|k|个单位；也可 以看顶点的坐标的移动, 顶点从（0，0）移到（h,k)，由此容易确定平移的方向和单位。 2.中考中的函数综合题，聊了灵活考查相关的基础知识外，还特别注重考查分析转化能力、 数形结合思想的运用能力以及探究能力．此类综合题，不仅综合了《函数及其图象》一章的 基本知识，还涉及方程（组）、不等式（组）及几何的许多知识点，是中考命题的热点．善 于根据数形结合的特点，将函数问题、几何问题转化为方程（或不等式）问题，往往是解题 的关键． ◆考点链接 1．点 A oyx ,0 在函数 cbxaxy  2 的图像上.则有 . 2. 求函数 bkxy  与 x 轴的交点横坐标，即令 ，解方程 ； 与 y 轴的交点纵坐标，即令 ，求 y 值 3. 求一次函数  0 knkxy 的图像 l 与二次函数  02  acbxaxy 的图像的交 点，解方程组 . 4．二次函数 cbxaxy  2 通过配方可得 2 2 4()24 b ac by a x aa    ， ⑴ 当 0a  时，抛物线开口向 ，有最 （填“高”或“低”）点, 当 x  时， y 有最 （“大”或“小”）值是 ； ⑵ 当 0a  时，抛物线开口向 ，有最 （填“高”或“低”）点, 当 时， 有最 （“大”或“小”）值是 ． 5. 每件商品的利润 P = － ；商品的总利润 Q = × . ◆典例精析 例 1（重庆市江津区）如图，反比例函数 xy 2 的图像与一次函数 bkxy  的图像交于点 A(ｍ，2)，点 B(－2, n )，一次函数图像与 y 轴的交点为 C。 - 5 - （1）求一次函数解析式； （2）求 C 点的坐标； （3）求△AOC 的面积。 解析：（1）确定一次函数的的关系式的关键是求出点 A、点 B 的坐标，分别把 A（m，2）， B （-2，n）代入反比例函数的关系式易求出 m=1、n=-1，由待定系数法确定出一次函数关系 式为 1yx的值； （2）令关系式 中的 x 为 0 求出 y=1，所以 C（0，1）； （3）△AOC 的面积等于 1 2 ×OC×1= . 解：由题意：把 A（m，2）， B（-2，n）代入 2y x 中得 1 1 m n    ∴A（1，2） B（-2，-1） 将 A.B 代入 y kx b中得 2 21 kb kb      1 1 k b    ∴一次函数解析式为： （2）C（0，1） - 6 - （3） 111122AOCS     例 2（内蒙古包头）某商场试销一种成本为每件 60 元的服装，规定试销期间销售单价不低 于成本单价，且获利不得高于 45%，经试销发现，销售量 y （件）与销售单价 x （元）符合 一次函数 y kx b，且 65x  时， 55y  ； 75x  时， 45y  ． （1）求一次函数 y kx b的表达式； （2）若该商场获得利润为W 元，试写出利润 与销售单价 x 之间的关系式；销售单价定 为多少元时，商场可获得最大利润，最大利润是多少元？ （3）若该商场获得利润不低于 500 元，试确定销售单价 x 的范围． 解析：（1）利用待定系数法确定出一次函数 的表达式； （2）利润 =每件的利润×销售件数，得 W 2( 90) 900x    ，根据二次函数的最值问题 确定单价为 90 元，最大利润为 900 元； （3）令 W=500，即 2500 180 7200xx    ，解得 1270 110xx， ，因为60 87x≤ ≤ ， 故单价定为 70 元. 解：（1）根据题意得 65 55 75 45. kb kb    ， 解得 1 120kb  ， ． 所求一次函数的表达式为 120yx   ． （2） ( 60) ( 120)W x x    2 180 7200xx    ， 抛物线的开口向下，当 90x  时，W 随 x 的增大而增大， 而 ， 当 87x  时， 2(87 90) 900 891W      ． 当销售单价定为 87 元时，商场可获得最大利润，最大利润是 891 元． （3）由 500W  ，得 ， 整理得， 2 180 7700 0xx   ，解得， ． - 7 - 由图象可知，要使该商场获得利润不低于 500 元，销售单价应在 70 元到 110 元之间，而 60 87x≤ ≤ ，所以，销售单价 x 的范围是 70 87x≤ ≤ ． 例 3（山东烟台） 某商场将进价为 2000 元的冰箱以 2400 元售出，平均每天能售出 8 台， 为了配合国家“家电下乡”政策的实施，商场决定采取适当的降价措施.调查表明：这种冰 箱的售价每降低 50 元，平均每天就能多售出 4 台． （1）假设每台冰箱降价 x 元，商场每天销售这种冰箱的利润是 y 元，请写出 y 与 x 之间 的函数表达式；（不要求写自变量的取值范围） （2）商场要想在这种冰箱销售中每天盈利 4800 元，同时又要使百姓得到实惠，每台冰 箱应降价多少元？ （3）每台冰箱降价多少元时，商场每天销售这种冰箱的利润最高？最高利润是多少？ 【解析】（1）利润=单价×销售件数，单价为（2400-2000-x），销售件数为(8 4 )50 x ； （2）令 y=4800，即 22 243200480025xx    ，解方程得 12100 200xx， ，老百姓 要想得到实惠，所以取 200x ； （3）利用二次函数的最值解决. 解：（1）根据题意，得 (24002000)8450 xyx    ， 即 22 24320025y x x   ． （2）由题意，得 ． 整理，得 2300200000xx  ． 解这个方程，得 ． 要使百姓得到实惠，取 ．所以，每台冰箱应降价 200 元． （3）对于 22 24320025y x x   ， 当 24 15022 25 x  时， 150(24002000150)8425020500050y 最大值 ． - 8 - 所以，每台冰箱的售价降价 150 元时，商场的利润最大，最大利润是 5000 元． ◆ 迎考精炼 一、选择题 1.（四川凉山州）若 0ab  ，则正比例函数 y ax 与反比例函数 by x 在同一坐标系中的 大致图象可能是（ ） 2．（黑龙江佳木斯）若关于ｘ的一元一次方程 2 2 1 0nx x   无实数根，则一次函数 ( 1)y n x n   的图像不经过（ ） A.第一象限 B. 第二象限 C. 第三象限 D. 第四象限 二、填空题 1．（湖北十堰）已知函数 1 xy 的图象与 x 轴、y 轴分别交于点 C.B，与双曲线 x ky  交 于点 A.D, 若 AB+CD= BC，则 k 的值为 ． 2．（内蒙古包头）如图，已知一次函数 1yx的图象与反比例函数 ky x 的图象在第一 象限相交于点 A ，与 x 轴相交于点C AB x， ⊥ 轴于点 B ， AOB△ 的面积为 1，则 AC 的 长为 （保留根号） ． 3．（青海）如图，函数 yx 与 4y x 的图象交于 A、B 两点，过点 A 作 AC 垂直于 y 轴，垂 足为 C，则 ABC△ 的面积为 ． y O x A C B y x O C． y x O A． y x O D． y x O B． - 9 - 三、解答题 1.（河南）如图，在平面直角坐标系中，已知矩形 ABCD 的三个顶点 B（4，0）、 C（8，0）、 D（8，8）.抛物线 y=ax2+bx 过 A、C 两点. (1)直接写出点 A 的坐标，并求出抛物线的解析式； (2)动点 P 从点 A 出发．沿线段 AB 向终点 B 运动，同时点 Q 从点 C 出发，沿线段 CD 向终点 D 运动．速度均为每秒 1 个单位长度，运动时间为 t 秒.过点 P 作 PE⊥AB 交 AC 于点 E ①过点 E 作 EF⊥AD 于点 F，交抛物线于点 G.当 t 为何值时，线段 EG 最长? ②连接 EQ．在点 P、Q 运动的过程中，判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的 t 值. 2.(贵州安顺)已知一次函数 ( 0)y kx b k   和反比例函数 2 ky x 的图象交于点 A(1，1) （1） 求两个函数的解析式； （2） 若点 B 是 x 轴上一点，且△AOB 是直角三角形，求 B 点的坐标。 3．（重庆綦江）如图，一次函数 y kx b( 0)k  的图象与反比例函数 ( 0)mymx的图 象相交于 A.B 两点． （1）根据图象，分别写出点 A.B 的坐标； （2）求出这两个函数的解析式． O A C B x y - 10 - 4.（辽宁锦州）某商场购进一批单价为 50 元的商品，规定销售时单价不低于进价，每件的 利润不超过40%.其中销售量y(件)与所售单价x(元)的关系可以近似的看作如图所表示的一 次函数. (1)求 y 与 x 之间的函数关系式，并求出 x 的取值范围； (2)设该公司获得的总利润(总利润=总销售额-总成本)为 w 元，求 w 与 x 之间的函数关 系式.当销售单价为何值时，所获利润最大？最大利润是多少？ 5．（安徽）已知某种水果的批发单价与批发量的函数关系如图（1）所示． （1）请说明图中①、②两段函数图象的实际意义． （2）写出批发该种水果的资金金额 w（元）与批发量 m（kg）之间的函数关系式；在下 图的坐标系中画出该函数图象；指出金额在什么范围内，以同样的资金可以批发到较多 数量的该种水果． O 60 20 4 批发单价（元） 5 批发量（kg） ① ② （1） 1 B A O x y 1 - 11 - （3）经调查，某经销商销售该种水果的日最高销量与零售价之间的函数关系如图（2） 所示，该经销商拟每日售出 60kg 以上该种水果，且当日零售价不变，请你帮助该经销 商设计进货和销售的方案，使得当日获得的利润最大． 6.（山东威海）一次函数 y ax b的图象分别与 x 轴、 y 轴交于点 ,MN，与反比例函数 ky x 的图象相交于点 ,AB．过点 A 分别作 AC x 轴， AE y 轴，垂足分别为 ,CE； 过点 B 分别作 BF x 轴，BD y 轴，垂足分别为 FD， ，AC 与 BD 交于点 K ，连接CD ． （1）若点 AB， 在反比例函数 的图象的同一分支上，如图 1，试证明： ① AEDK CFBKSS四边形 四边形 ； ② AN BM ． （2）若点 AB， 分别在反比例函数 的图象的不同分支上，如图 2，则 AN 与 BM 还相等吗？试证明你的结论． 7. （ 山东泰安）如 图 ， △ OAB 是 边 长 为 2 的 等 边 三 角 形 ， 过 点 A 的 直 线 金额 w（元） O 批发量 m（kg） 300 200 100 20 40 60 O 6 2 40 日最高销量（kg） 80 零售价（元） （2） 4 8 （6，80） （7，40） O C F M D E N K y x 11()A x y， 22()B x y， （图 1） O C D K F E N y x 33()B x y， M （图 2） - 12 - 。轴交于点与 Exmxy  3 3 （1） 求点 E 的坐标； （2） 求过 A.O、E 三点的抛物线解析式； （3） 若点 P 是（2）中求出的抛物线 AE 段上一动点（不与 A.E 重合），设四边形 OAPE 的面 积为 S，求 S 的最大值。 8．（湖北黄石）为了扩大内需，让惠于农民，丰富农民的业余生活，鼓励送彩电下乡，国家 决定对购买彩电的农户实行政府补贴．规定每购买一台彩电，政府补贴若干元，经调查某商 场销售彩电台数 y （台）与补贴款额 x（元）之间大致满足如图①所示的一次函数关系．随 着补贴款额 x 的不断增大，销售量也不断增加，但每台彩电的收益 Z（元）会相应降低且 与 x 之间也大致满足如图②所示的一次函数关系． （1）在政府未出台补贴措施前，该商场销售彩电的总收益额为多少元？ （2）在政府补贴政策实施后，分别求出该商场销售彩电台数 y 和每台家电的收益 与政府 补贴款额 x 之间的函数关系式； （3）要使该商场销售彩电的总收益 w （元）最大，政府应将每台补贴款额 x 定为多少？并 求出总收益 w 的最大值． 9.（内蒙古包头）已知二次函数 2y ax bxc  （ 0a  ）的图象经过点 (1 0)A ， ， (2 0)B ， ， (0 2)C ， ，直线 xm （ 2m ）与 x 轴交于点 D ． （1）求二次函数的解析式； 1200 800 0 400 y(台) x(元) z(元) x(元) 200 160 200 0 图① 图② - 13 - （2）在直线 xm （ 2m ）上有一点 E （点在第四象限），使得E DB、、为顶点的三角形与 以 AOC、、为顶点的三角形相似，求点坐标（用含 m 的代数式表示）； （3）在（2）成立的条件下，抛物线上是否存在一点 F ，使 得四边形 ABEF 为平行四边形？ 若存在，请求出 m 的值及四边形 ABEF 的面积；若不存在，请说明理由． 10.(四川成都)已知一次函数 2yx与反比例函数 ky x ，其中一次函数 的图 象经过点 P( k ，5)． (1)试确定反比例函数的表达式； (2)若点 Q 是上述一次函数与反比例函数图象在第三象限的交点，求点 Q 的坐标． y x O - 14 - 【参考答案】 一、选择题 1.B 2.Ｃ 二、填空题 1. 3 4 2. 22 3.4 三、解答题 1.(1)点 A 的坐标为（4，8） 将 A(4,8)、C（8，0）两点坐标分别代入 y=ax2+bx 8=16a+4b 得 0=64a+8b 解 得 a=- 1 2 ,b=4 ∴抛物线的解析式为：y=- x2+4x （2）①在 Rt△APE 和 Rt△ABC 中，tan∠PAE= PE AP = BC AB ,即 = 4 8 ∴PE= AP= t．PB=8-t． ∴点Ｅ的坐标为（4+ t，8-t）. ∴点 G 的纵坐标为：- （4+ t）2+4（4+ t）=- 1 8 t2+8. ∴EG=- t2+8-(8-t) =- t2+t. ∵- ＜0，∴当 t=4 时，线段 EG 最长为 2. ②共有三个时刻. t1=16 3 ， t2= 40 13 ，t3= 85 25 ． 2.（1）∵点 A（1，1）在反比例函数 x2 ky  的图象上, ∴k=2．∴反比例函数的解析式为： x 1y  ． - 15 - 一次函数的解析式为： bx2y  ． ∵点 A（1，1）在一次函数 的图象上 ∴ 1b  ． ∴一次函数的解析式为 1x2y  （2）∵点 A（1，1） ∴∠AOB=45o． ∵△AOB 是直角三角形 ∴点 B 只能在 x 轴正半轴上． ① 当∠OB1A=90 o 时，即 B1A⊥OB1. ∵∠AOB1=45o ∴B1A= OB1 ． ∴B1（1，0）． ② 当∠O A B2=90 o 时，∠AOB2=∠AB2O=45o, ∴B1 是 OB2 中点, ∴B2（2，0）． 综上可知，B 点坐标为（1，0）或（2，0）． 3.（1）解：由图象知，点 A 的坐标为( 6 1)， ， 点 B 的坐标为（3，2） （2）∵反比例函数 my x 的图象经过点 ， ∴ 2 3 m ，即 6m  ． ∴所求的反比例函数解析式为 6y x ． ∵一次函数 y kx b的图象经过 、 两点， ∴ 16 23 kb kb       解这个方程组，得 1 3 1 k b     ∴所求的一次函数解析式为 1 13yx． 4.解(1) 最高销售单价为 50(1+40%)=70(元). 根据题意，设 y 与 x 的函数关系式为 y=kx+b(k≠0). ∵函数图象经过点(60，400)和(70，300)， ∴ 解得 - 16 - ∴y 与 x 之间的函数关系式为 y=-10x+1000， x 的取值范围是 50≤x≤70. (2)根据题意，w=(x-50)(-10x+1000)， W=-10x2+1500x-50000,w=-10(x-75)2+6250. ∵a=-10 ，∴抛物线开口向下. 又∵对称轴是 x=75，自变量 x 的取值范围是 50≤x≤70 ， ∴y 随 x 的增大而增大. ∴当 x=70 时，w 最大值=-10(70-75)2+6250=6000(元). ∴当销售单价为 70 元时，所获得利润有最大值为 6000 元. 5.（1）解：图①表示批发量不少于 20kg 且不多于 60kg 的该种水果， 可按 5 元/kg 批发；……3 分 图②表示批发量高于 60kg 的该种水果，可按 4 元/kg 批发． （2）解：由题意得： 20 60 60 5 4 mm w mm    ≤ ≤（ ） ）＞（ ，函数图象如图所示． 由图可知资金金额满足 240＜w≤300 时，以同样的资金可 批发到较多数量的该种水果． （3）解法一： 设当日零售价为 x 元，由图可得日最高销量 320 40wm 当 m＞60 时，x＜6.5 由题意，销售利润为 2( 4)(320 40 ) 40[ ( 6) 4]y x m x       当 x＝6 时， 160y 最大值 ，此时 m＝80 即经销商应批发 80kg 该种水果，日零售价定为 6 元/kg， 当日可获得最大利润 160 元． 解法二： 设日最高销售量为 xkg（x＞60） 则由图②日零售价 p 满足： 320 40xp ，于是 320 40 xp  销售利润 2320 1( 4) ( 80) 16040 40 xy x x      - 17 - 当 x＝80 时， 160y 最大值 ，此时 p＝6 即经销商应批发 80kg 该种水果，日零售价定为 6 元/kg，当日可获得最大利润 160 元． 6.（1）① AC x⊥ 轴， AE y⊥ 轴， 四边形 AEOC 为矩形． BF x⊥ 轴， BD y⊥ 轴， 四边形 BDOF 为矩形． AC x⊥ 轴， BD y⊥ 轴， 四边形 AEDK DOCK CFBK， ， 均为矩形． 1 1 1 1OC x AC y x y k  ， ， ， 11AEOCS OC AC x y k  矩形 2 2 2 2OF x FB y x y k  ， ， ， 22BDOFS OF FB x y k  矩形 ． AEOC BDOFSS矩形 矩形 ． AEDK AEOC DOCKS S S矩形 矩形 矩形 ， CFBK BDOF DOCKS S S矩形 矩形 矩形 ， AEDK CFBKSS矩形 矩形 ． ②由（1）知 ． AK DK BK CK ． AK BK CK DK ． 90AKB CKD    °， AKB CKD△ ∽△ ． CDK ABK   ． AB CD∥ ． AC y∥ 轴， 四边形 ACDN 是平行四边形． - 18 -  AN CD ． 同理 BM CD ． AN BM ． （2） AN 与 BM 仍然相等． AEDK AEOC ODKCS S S矩形 矩形 矩形 ， BKCF BDOF ODKCS S S矩形 矩形 矩形 ， 又 AEOC BDOFS S k矩形 矩形 ， AEDK BKCFSS矩形 矩形 ． AK DK BK CK ． CK DK AK BK ． KK   ， CDK ABK△ ∽△ ． CDK ABK   ． AB CD∥ ． AC y∥ 轴， ∴四边形 ANDC 是平行四边形． ∴ AN CD ． 同理 BM CD ． ∴ AN BM ． 7.解：（1）作 AF⊥x 轴与 F ∴OF=OAcos60°=1，AF=OFtan60°= 3 ∴点 A（1， 3 ） 代入直线解析式，得 313 3  m ，∴m= 3 34 ∴ 3 34 3 3  xy - 19 - 当 y=0 时， 03 34 3 3  x 得 x=4， ∴点 E（4，0） （2） 设过 A.O、E 三点抛物线的解析式为 cbxaxy  2 ∵抛物线过原点 ∴c=0 ∴ ∴ ∴抛物线的解析式为 xxy 3 34 3 3 2  （3）作 PG⊥x 轴于 G，设 )( 00 yxP ， 2 )4( 2 )1)(3( 2 3 0000 yxxySSSS PGEFGPAOG  △△△ )353(2 1)33(2 1 0 2 000 xxyx  8 325)2 5(2 3 2 0  x 当 38 25 2 5 0  最大时，Sx 8.解：（1）该商场销售家电的总收益为800 200 160000 （元） （2）依题意可设 - 20 - 1 800y k x ， 2 200Z k x 有 1400 800 1200k  ， 2200 200 160k ， 解得 12 11 5kk  ， ． 所以 800yx ， 1 2005Zx   ． （3） 1( 800) 2005W yZ x x     21 ( 100) 1620005 x    政府应将每台补贴款额 x 定为 100 元，总收益有最大值． 其最大值为162000元． 9.解析：本题考查二次函数关系式求法、坐标系中有关线段的长度与点的坐标之间的关系， 探究三角形相似的条件和判定四边形为平行四边形的条件，涉及到一元二次方程的解法等 综合性较强，稍有疏忽就容易失分。 解：(1)根据题意，得 0 4 2 0 2 abc a b c c          ，解得 1 3 2 a b c      ∴ 2 32y x x  。 (2)当Δ EDB∽Δ AOC 时，得 AO CO ED BD 或 AO CO BD ED 。 ∵AO=1，CO=2，BD=m-2，当 AO CO ED BD 时，得 12 2ED m  ， ∴ 2 2 mED  。 ∵点 E 在第四象限， ∴ 1 2, 2 mEm  ，当 AO CO BD ED 时，得 12 2m ED ，∴ 24EDm， ∵点 E 在第四象限， ∴  1 ,42Em m 。 (3)假设抛物线上存在一点这 P，使得四边形 ABEF 为平行四边形，则 EF=AB=1，点 F 的横坐 标为 m-1,当点 1E 的坐标为 2, 2 mm   时，点 1F 的坐标为 21, 2 mm  ， ∵点 1F 在抛物线的图象上， ∴    22 13 122 mmm ， ∴ 22 11140mm ， ∴  2 7 20mm  ∴ 7,22mm(舍去) - 21 - ∴ 1 53,24F  ， ∴ 331 44ABEFS   。 当点 2E 的坐标为 ,4 2mm 时，点 2F 的坐标为 1,42mm ， ∵点 F2 在抛物线的图象 上， ∴    242 1312,mm m ∴ 2 7 100,mm   ∴  2 5 0mm  ∴ 2m (舍去)， 5m ∴  1 4, 6 ,F  ∴ 166ABEFS 平行四边形 点拨：（2）中讨论Δ EDB 与Δ AOC 相似的条件时，题目中未用相似符号连接应按不同的 对应关系分情况讨论，否则易漏解。在由线段的长度求 E 点坐标时要注意点的坐标的符号。 （3）中在求是否存在点 E 问题，应先假设存在，列得关系式如果有解，并且符合题意就存 在；如果无解或解得的结果不符合题意，就不存在. 10.（1）∵一次函数 y=x+2 的图像经过点 P ∴5=k+2 ∴k=3 ∴反比例函数解析式为 y= x 3 (2)由      xy xy 3 2 ，解得      1 3 y x 或      1 3 y x ∵点 Q 在第三象限 ∴Q(-3，-1)