2010年山东省泰安市中考数学真题

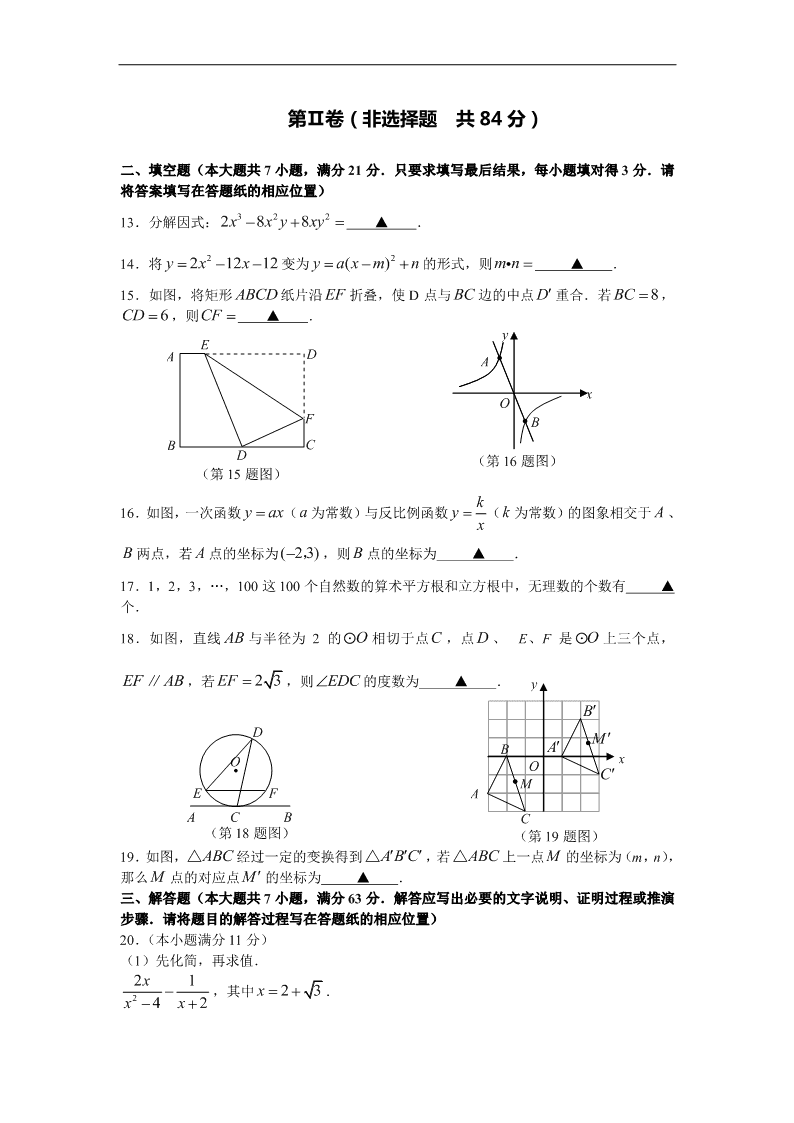
2010年山东省泰安市中考数学真题

试卷类型：A 泰安市二○一○年初中学生学业考试 数 学 试 题 本试题分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分．第Ⅰ卷 1 至 2 页，第Ⅱ卷 3 至 5 页，共 120 分．考试时间 120 分钟． 第Ⅰ卷（选择题 共 36 分） 注意事项： 1．答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目、试题类型涂、写在答 题卡上． 2．第Ⅰ卷每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动， 用橡皮擦干净后，再选涂其他答案标号． 3．答案答在试题上无效．考试结束后，试题和答题卡一并收回． 一、选择题（本大题共 12 小题，在每小题给出的四个选项中，只有一个是正确的，请把正 确的选项选出来，每小题选对得 3 分，选错、不选或选出的答案超过一个，均记零分） 1．| 5| 的倒数是（ ） A． 5 B． 1 5 C．5 Ｄ． 1 5 2．计算 32()a · 3a 的结果是（ ） A． 8a B． 9a C． 10a Ｄ． 18a 3．下列图形： A． B． C． Ｄ． 其中，既是轴对称图形，又是中心对称图形的个数是（ ） A．1 个 B．2 个 C．3 个 Ｄ．4 个 4．函数 21yx与函数 ky x 的图象相交于点(2 )m， ，则下列各点不在．．函数 的图 象上的是（ ） A．( 2 5)， B． 5( 4)2 ， C．( 110) ， Ｄ．(5 2)， 1 l1 l2 l3 l4 2 （第 5 题图） 5．如图 1 2 3 4 1 42l l l l ∥ ， ⊥ ， ，那么 2 的度数为（ ） A．48° B．42° C．38° Ｄ．21° 6．如图，数轴上 A 、 B 两点对应的实数分别为 a，b， 则下列结论不正确．．．的是（ ） A． 0ab B． 0ab  C． 0ab Ｄ．| | | | 0ab 7．如图是某几何体的三视图，则该几何体的全面积是（ ） A．36π B．60π C．96π Ｄ．120π 8．下列函数：① 3yx ② 21yx ③ 1 ( 0)yxx   ④ 2 23y x x    ，其中 y 的值随 x 值的增大而增大的函数有 （ ） A．4 个 B．3 个 C．2 个 Ｄ．1 个 9．如图，E 是□ ABCD的边 AD 的中点，CE 与 BA 的延长线交于 点 F ，若 FCD D   ，则下列结论不成立．．．的是（ ） A． AD CF B． BF CF C． AF CD Ｄ． DE EF 10．如图所示的两个转盘，每个转盘均被分成四个相 同的扇形，转动转盘时指针落在每一个扇形内的机会 均等，同时转动两个转盘，则两个指针同时落在标有 奇数扇形内的概率为（ ） A． 1 2 B． 1 3 C． 1 4 Ｄ． 1 8 11．若关于 x 的不等式 0 7 2 1 xm x    ， ≤ 的整数解共有 4 个，则 m 的取值范围是（ ） A．67m B．67m ≤ C．67m≤ ≤ Ｄ．67m ≤ 12．如图，矩形 ABCD的两对角线 AC 、 BD 交于点O ， 60AOB，设 cmAB x ， 矩形 ABCD的面积为 2cms ，则变量 s 与 x 之间的函数关系式为（ ） A． 23sx B． 23 3sx C． 23 3sx Ｄ． 21 2sx 1 1 2 0 B A （第 6 题图） 12 ８ （第 7 题图） F D E C B A （第 9 题图） 1 2 3 4 7 8 5 6 （第 10 题图） O D C A B （第 12 题图） 第Ⅱ卷（非选择题 共 84 分） 二、填空题（本大题共 7 小题，满分 21 分．只要求填写最后结果，每小题填对得 3 分．请 将答案填写在答题纸的相应位置） 13．分解因式： 3 2 22 8 8x x y xy   ▲ ． 14．将 22 12 12y x x   变为 2()y a x m n   的形式，则 mn ▲ ． 15．如图，将矩形 ABCD纸片沿 EF 折叠，使 D 点与 BC 边的中点 D 重合．若 8BC  ， 6CD  ，则CF  ▲ ． 16．如图，一次函数 y ax （ a 为常数）与反比例函数 ky x （ k 为常数）的图象相交于 A 、 B 两点，若 A 点的坐标为( 2 3) ， ，则 点的坐标为 ▲ ． 17．1，2，3，…，100 这 100 个自然数的算术平方根和立方根中，无理数的个数有 ▲ 个． 18．如图，直线 AB 与半径为 2 的 O 相切于点 C ，点 D 、 E、F 是 上三个点， EF AB∥ ，若 23EF  ，则 EDC 的度数为 ▲ ． 19．如图， ABC△ 经过一定的变换得到 ABC  △ ，若 上一点 M 的坐标为（m，n）， 那么 点的对应点 M 的坐标为 ▲ ． 三、解答题（本大题共 7 小题，满分 63 分．解答应写出必要的文字说明、证明过程或推演 步骤．请将题目的解答过程写在答题纸的相应位置） 20．（本小题满分 11 分） （1）先化简，再求值． 2 21 42 x xx ，其中 23x  ． A E D F C D B （第 15 题图） y x O A B （第 16 题图） y x O B A C A B C M （第 19 题图） M O F D E A C B （第 18 题图） （2）解方程： (3 2)( 3) 14x x x    ． 21．（本小题满分 8 分） 某中学为了了解本校初三学生体育成线，从本校初三 1200 名学生中随机抽取了部分学生进 行测试，并将测试成绩（满分 100 分，成绩均取整数）进行统计，绘制成如下图表（部分）： 组别 成绩 频数 频率 1 90.5— 100.5 8 0.08 2 80.5—90.5 m 0.24 3 70.5—80.5 40 n 4 60.5—70.5 25 0.25 5 50.5—60.5 3 0.03 合计 / / / 请根据上面的图形，解答下列各题： （1）m= ，n= ； （2）补全频数分布直方图； （3）指出这组数据的“中位数”落在哪一组（不要求说明理由）； （4）若成绩 80 分以上的学生为优秀，请估计该校初三学生体育成绩优秀的人数． 22．（本小题满分 8 分） 某电视机厂要印制产品宣传材料，甲印刷厂提出：每份材料收 1 元印刷费，另收 1000 元制 版费；乙厂提出：每份材料收 2 元印刷费，不收制版费． （1）分别写出两厂的收费 y（元）与印制数量 x（份）之间的函数关系式； （2）电视机厂拟拿出 3000 元用于印刷宣传材料，找哪家印刷厂印制的宣传材料能多一些？ （3）印刷数量在什么范围时，在甲厂印制合算？ 23．（本小题满分 8 分） 如图，在 ABC△ 中，D是BC边上一点，E是AC边上一点，且满足 AD AB ADE C   ， ． （1）求证： AED ADC DEC B     ， ； （2）求证： 2AB AE AC ． A E C D B （第 23 题图） 40 32 24 16 8 0 50.5 60.5 70.5 80.5 90.5 100.5 频数 频数分布直方图 成绩 （第 21 题图） 24．（本小题满分 8 分） 某商店经销一种泰山旅游纪念品，4 月份的营业额为 2000 元，为扩大销售量，5 月份该商店 对这种纪念品打 9 折销售，结果销售量增加 20 件，营业额增加 700 元． （1）求该种纪念品 4 月份的销售价格； （2）若 4 月份销售这种纪念品获利 800 元，5 月份销售这种纪念品获利多少元？ 25．（本小题满分 10 分） 如图， ABC△ 是等腰直角三角形， 90A ，点 P、Q 分别是 AB、AC 上的动点，且满足 BP AQ ，D 是 BC 的中点． （1）求证： PDQ△ 是等腰直角三角形； （2）当点 P 运动到什么位置时，四边形 APDQ 是正方形，并说明理由． 26．（本小题满分 10 分） 如图， 是等腰三角形， AB AC ，以 AC 为直径的 O 与 BC 交于点 D ， DE AB⊥ ，垂足为 E ， ED 的延长线与 AC 的延长线交于点 F ． （1）求证： DE 是 的切线； （2）若 的半径为 2， 1BE  ，求cos A的值． A Q C D B P （第 25 题图） F C D B E A O （第 26 题图）