2012年山东省济宁市中考数学真题

2012年山东省济宁市中考数学真题

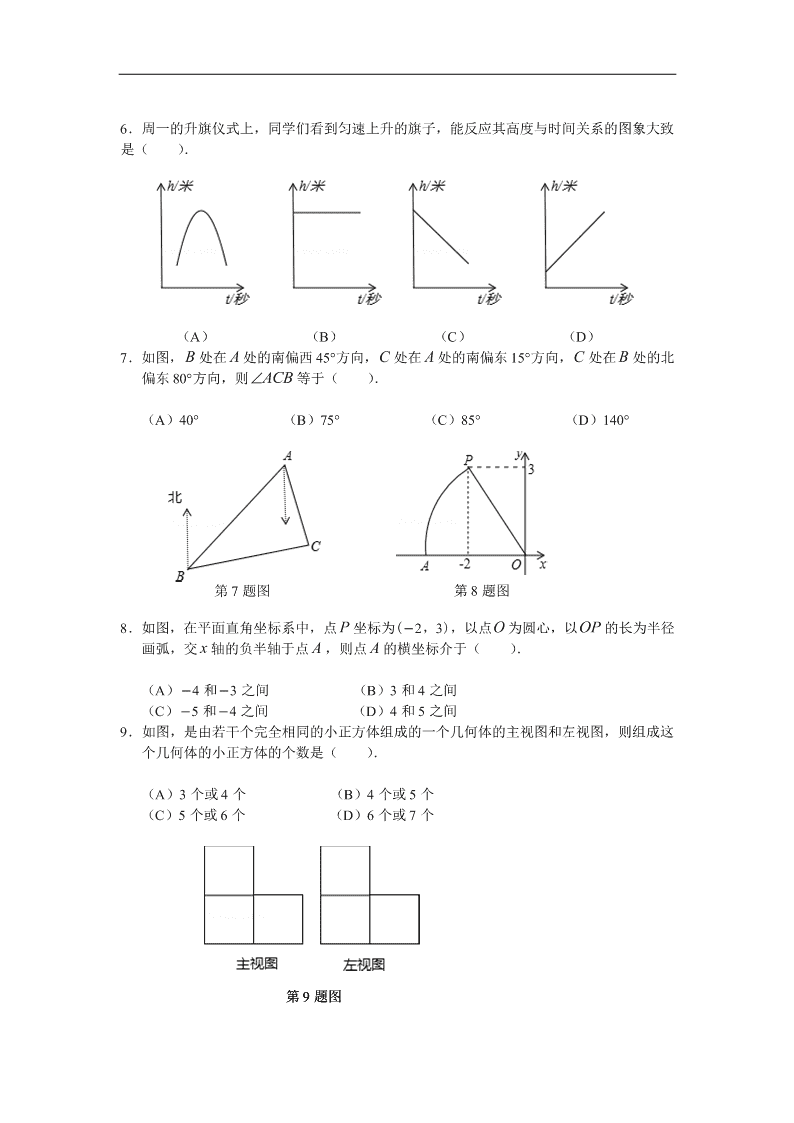
济宁市二 O 一二年高中阶段学校招生考试 数 学 试 题 注意事项： 1．本试题分第Ⅰ卷和第Ⅱ卷两部分，共 10 页.第Ⅰ卷 2 页为选择题，30 分；第Ⅱ卷 8 页为非选择题，70 分；共 100 分.考试时间为 120 分钟. 2．答第Ⅰ卷前务将自己的性名、考号、考试科目涂写在答题卡上，每题选出答案后， 都必须用 2B 铅笔把答题卡上对应题目的答案标号（ABCD）涂黑，如需改动，必须先用橡 皮擦干净，再改涂其他答案. 3．答第Ⅱ卷时，将密封线内的项目填写清楚，并将座号填写在第 8 页右侧，用钢笔或 圆珠笔直接答在试卷上.考试结束，试题和答题卡一并收回. 第Ⅰ卷（选择题 共 30 分） 一、选择题（下列各题的四个选项中，只有一项符合题意，每小题 3 分，共 30 分） 1．在数轴上到原点距离等于 2 的点所标示的数是（ ）． （A） 2 （B） 2 （C） 2 （D）不能确定 2．下列运算正确的是（ ）． （A）  2 3 1 6 1xx     （B）  2 3 1 6 1xx     （C）  2 3 1 6 2xx     （D）  2 3 1 6 2xx     3．空气是由多种气体混合而成的，为了简明扼要的介绍空气的组成情况，较好的描述数据， 最适合．．．使用的统计图是（ ）． （A）扇形图 （B）条形图 （C）折线图 （D）直方图 4．下列式子变形是因式分解的是（ ）． （A）  2 5 6 5 6x x x x     （B）   2 5 6 2 3x x x x     （C）   22 3 5 6x x x x     （D）   2 5 6 2 3x x x x     5．用直尺和圆规作一个角的平分线的示意图如图所示，则能说明 AOC BOC   的依据 是（ ）． （A）SSS （B） ASA （C） AAS （D）角平分线上的点到角两边距离相等 第5题图 6．周一的升旗仪式上，同学们看到匀速上升的旗子，能反应其高度与时间关系的图象大致 是（ ）． （A） （B） （C） （D） 7．如图， B 处在 A 处的南偏西 45°方向，C 处在 A 处的南偏东 15°方向，C 处在 B 处的北 偏东 80°方向，则 ACB 等于（ ）． （A）40° （B）75° （C）85° （D）140° 8．如图，在平面直角坐标系中，点 P 坐标为( 2，3)，以点O 为圆心，以OP 的长为半径 画弧，交 x 轴的负半轴于点 A ，则点 A 的横坐标介于（ ）． （A） 4 和 3 之间 （B）3 和 4 之间 （C） 5 和 4 之间 （D）4 和 5 之间 9．如图，是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图，则组成这 个几何体的小正方体的个数是（ ）． （A）3 个或 4 个 （B）4 个或 5 个 （C）5 个或 6 个 （D）6 个或 7 个 第 7 题图 第 8 题图 第 9 题图 第 9 题图 10．如图，将矩形 ABCD的四个角向内折起，恰好拼成一个无缝隙无重叠的四边形 EFGH ， 若 12EH  厘米， 16EF  厘米，则边 AD 的长是（ ）． （A）12 厘米 （B）16 厘米 （C）20 厘米 （D）28 厘米 济宁市二 O 一年高中阶段学校招生考试 数 学 试 题 二、填空题（每小题 3 分，共 15 分；只要求填写最后结果） 11．某种苹果的售价是每千克 x 元，用面值为 100 元的人民币购买了 5 千克，应找回 元． 12．数学课上，小明拿出了连续五日最低气温的统计表： 日期 一 二 三 四 五 最低气温(℃) 22 24 26 23 25 那么，这组数据的平均数和极差分别是 ． 13．在 ABC△ 中，若 A 、 B 满足， 2 12cos sin 022AB    ，则 C ＝ ． 14．如图，是反比例函数 2ky x  的图象的一个分支，对于给出的下列 说法： ①常数 k 的取值范围是 2k  ； ②另一个分支在第三象限； ③在函数图象上取点  11A a b， 和点  22B a b， ，当 12aa 时，则 12bb ； ④在函数图象的某一个分支上取点 和点 ，当 时，则 ； 其中正确的是 (在横线上填出正确的序号) 第 10 题图 第 14 题图 15．如图，在等边三角形 ABC 中，D 是 BC 边上的一点，延长 AD 至 E ， 使 AE AC ， BAE 的平分线交 ABC△ 的高 BF 于点O ，则 tan AEO ＝ ． 三、解答题（共 55 分，解答应写出文字说明、证明过程或推演步骤） 16．（5 分）解不等式组   5 2 3 1 5 x x xx     ， ≤ ， 并在数轴上表示出它的解集． 17．（5 分）如图， AD 是 ABC△ 的角平分线，过点 D 作 DE AB∥ ，DF AC∥ ，分别交 AC 、 AB 于点 E 和 F ． （1）在图中画出线段 DE 和 DF ； （2）连接 EF ，则线段 AD 和 EF 互相垂直平分，这是为什么？ 18．（6 分）一学校为了绿化校园环境，向某园林公司购买了一批树苗，园林公司规定：如 果购买树苗不超过 60 棵，每棵售价为 120 元；如果购买树苗超过 60 棵，每增加 1 棵， 所出售的这批树苗每棵售价均降低 0.5 元，但每棵树苗最低售价不得少于 100 元，该校 最终向园林公司支付树苗款 8 800 元，请问该校共购买了多少棵树苗？ 第 15 题图 第 17 题图 19．（6 分）问题情境： 用同样大小的黑色棋子按如图所示的规律摆放，则第 2012 个图共有多少枚棋子？ 建立模型： 有些规律问题可以借助函数思想来探讨，具体步骤：第一步，确定变量；第二步：在直 角坐标系中画出函数图象；第三步：根据函数图象猜想并求出函数关系式；第四步：把 另外的某一点代入验证，若成立，则用这个关系式去求解． 解决问题： 根据以上步骤，请你解答“问题情境”． 第 19 题图 第 19 题图 20．（7 分）如图， AB 是 O⊙ 的直径， AC 是弦，OD AC 于点 D ，过点 A 作 O⊙ 的切 线 AP ， 与OD 的延长线交于点 P ，连接 PC 、 BC . （1）猜想：线段 与 BC 有何数量和位置关系，并证明你的结论． （2）求证： PC 是 O⊙ 的切线． 21．（8 分）如图，在平面直角坐标系中，有一 Rt ABC△ ，且  13A  ， ，  31B ， ，  33C  ， ， 已知 11A AC△ 是由 ABC△ 旋转得到的． （1）请写出旋转中心的坐标是 ，旋转角是 度； （2）以（1）中的旋转中心为中心，分别画出 顺时针旋转 90°、180°的三角形； （3）设 Rt ABC△ 两直角边 BC a 、 AC b 、 AC b 、斜边 AB c ，利用变换 前后所形成的图案证明勾股定理． 第 20 题图 第 21 题图 22．（8 分）有四张形状、大小和质地相同的卡片 A 、 B 、C 、D ，正面分别写有一个正多 边形(所有正多边形的边长相等)，把四张卡片洗匀后正面朝下放在桌面上，从中随机抽 取一张(不放回)，接着再随机抽取一张． （1）请你用画树形图或列表的方法列举出可能出现的所有结果； （2）如果在（1)中各种结果被选中的可能性相同，求两次抽取的正多边形能构成平面 镶嵌的概率； （3）若两种正多边形构成平面镶嵌， p 、 q 表示这两种正多边形的个数， x 、 y 表示 对应正多边形的每个内角的度数，则有方程 360px qy ，求每种平面镶嵌中 p 、q 的值． 23．（10 分）如图，抛物线 2 4y ax bx   与 x 轴交于  40A ， 、  20B  ， 两点，与 y 轴交 于点C ，点 P 是线段 AB 上一动点(端点除外)，过点 P 作 PD AC∥ ，交 BC 于点 D ， 连接CP ． （1）求该抛物线的解析式； （2）当动点 运动到何处时， 2BP BD BC · ； （3）当 PCD△ 的面积最大时，求点 的坐标． 第 22 题图 第 23 题图