2020全国中考数学试卷分类汇编专题40 动态问题

2020全国中考数学试卷分类汇编专题40 动态问题

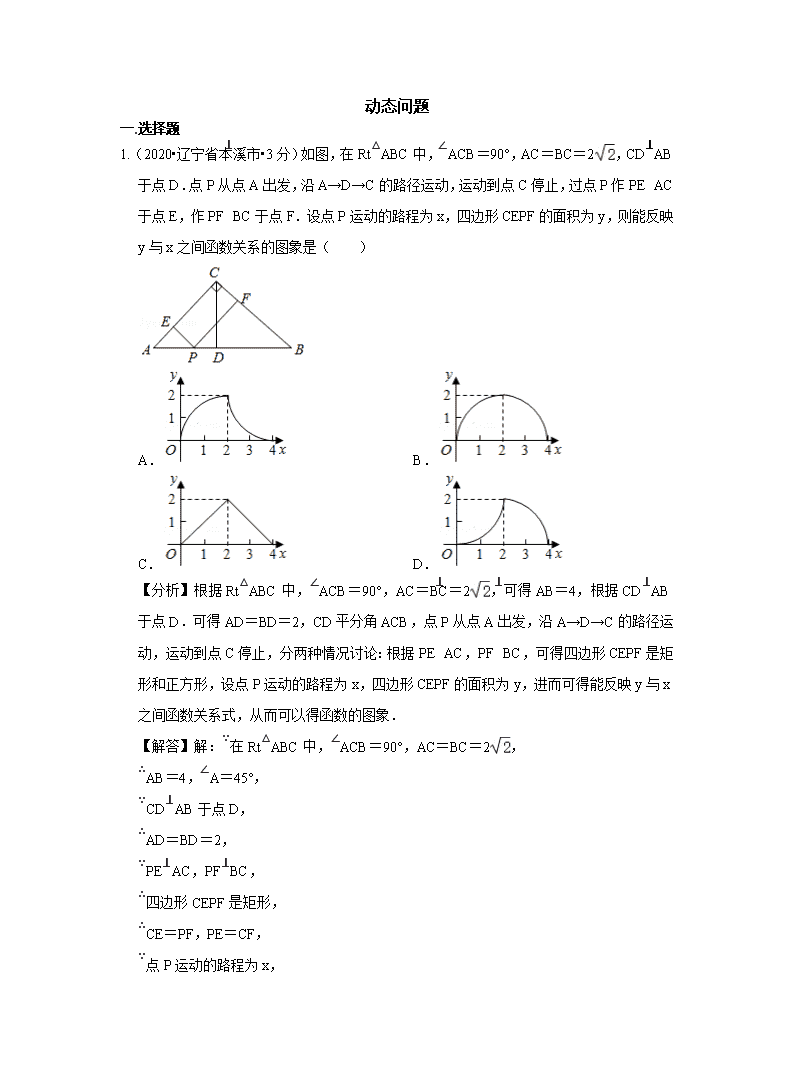
动态问题 一.选择题 ‎ ‎1.（2020•辽宁省本溪市•3分）如图，在Rt△ABC中，∠ACB＝90°，AC＝BC＝2，CD⊥AB于点D．点P从点A出发，沿A→D→C的路径运动，运动到点C停止，过点P作PE⊥AC于点E，作PF⊥BC于点F．设点P运动的路程为x，四边形CEPF的面积为y，则能反映y与x之间函数关系的图象是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据Rt△ABC中，∠ACB＝90°，AC＝BC＝2，可得AB＝4，根据CD⊥AB于点D．可得AD＝BD＝2，CD平分角ACB，点P从点A出发，沿A→D→C的路径运动，运动到点C停止，分两种情况讨论：根据PE⊥AC，PF⊥BC，可得四边形CEPF是矩形和正方形，设点P运动的路程为x，四边形CEPF的面积为y，进而可得能反映y与x之间函数关系式，从而可以得函数的图象．‎ ‎【解答】解：∵在Rt△ABC中，∠ACB＝90°，AC＝BC＝2，‎ ‎∴AB＝4，∠A＝45°，‎ ‎∵CD⊥AB于点D，‎ ‎∴AD＝BD＝2，‎ ‎∵PE⊥AC，PF⊥BC，‎ ‎∴四边形CEPF是矩形，‎ ‎∴CE＝PF，PE＝CF，‎ ‎∵点P运动的路程为x，‎ ‎∴AP＝x，‎ 则AE＝PE＝x•sin45°＝x，‎ ‎∴CE＝AC﹣AE＝2﹣x，‎ ‎∵四边形CEPF的面积为y，‎ ‎∴当点P从点A出发，沿A→D路径运动时，‎ 即0＜x＜2时，‎ y＝PE•CE ‎＝x（2﹣x）‎ ‎＝﹣x2+2x ‎＝﹣（x﹣2）2+2，‎ ‎∴当0＜x＜2时，抛物线开口向下；‎ 当点P沿D→C路径运动时，‎ 即2≤x＜4时，‎ ‎∵CD是∠ACB的平分线，‎ ‎∴PE＝PF，‎ ‎∴四边形CEPF是正方形，‎ ‎∵AD＝2，PD＝x﹣2，‎ ‎∴CP＝4﹣x，‎ y＝（4﹣x）2＝（x﹣4）2．‎ ‎∴当2≤x＜4时，抛物线开口向上，‎ 综上所述：能反映y与x之间函数关系的图象是：A．‎ 故选：A．‎ ‎【点评】本题考查了动点问题的函数图象，解决本题的关键是掌握二次函数的性质．‎ ‎2.（2020•山东淄博市•4分）如图1，点P从△ABC的顶点B出发，沿B→C→A匀速运动到点A，图2是点P运动时，线段BP的长度y随时间x变化的关系图象，其中M是曲线部分的最低点，则△ABC的面积是（　　）‎ A．12 B．24 C．36 D．48‎ ‎【分析】由图2知，AB＝BC＝10，当BP⊥AC时，y的值最小，即△ABC中，BC边上的高为8（即此时BP＝8），即可求解．‎ ‎【解答】解：由图2知，AB＝BC＝10，‎ 当BP⊥AC时，y的值最小，即△ABC中，BC边上的高为8（即此时BP＝8），‎ 当y＝8时，PC＝＝＝6，‎ ‎△ABC的面积＝×AC×BP＝8×12＝48，‎ 故选：D．‎ ‎【点评】本题是运动型综合题，考查了动点问题的函数图象、解直角三角形、图形面积等知识点．解题关键是深刻理解动点的函数图象，了解图象中关键点所代表的实际意义，理解动点的完整运动过程．‎ ‎3. （2020•安徽省•4分）如图，△ABC和△DEF都是边长为2的等边三角形，它们的边BC，EF在同一条直线l上，点C，E重合．现将△ABC在直线l向右移动，直至点B与F重合时停止移动．在此过程中，设点C移动的距离为x，两个三角形重叠部分的面积为y，则y随x变化的函数图象大致为（　　）‎ A． ‎ B． ‎ C． ‎ D．‎ ‎【分析】分为0＜x≤2.2＜x≤4两种情况，然后依据等边三角形的性质和三角形的面积公式可求得y与x的函数关系式，于是可求得问题的答案．‎ ‎【解答】解：如图1所示：当0＜x≤2时，过点G作GH⊥BF于H．‎ ‎∵△ABC和△DEF均为等边三角形，‎ ‎∴△GEJ为等边三角形．‎ ‎∴GH＝EJ＝x，‎ ‎∴y＝EJ•GH＝x2．‎ 当x＝2时，y＝，且抛物线的开口向上．‎ 如图2所示：2＜x≤4时，过点G作GH⊥BF于H．‎ y＝FJ•GH＝（4﹣x）2，函数图象为抛物线的一部分，且抛物线开口向上．‎ 故选：A．‎ ‎【点评】本题主要考查的是动点问题的函数图象，求得函数的解析式是解题的关键．‎ 二.填空题 ‎1.（2020•辽宁省营口市•3分）如图，△ABC为等边三角形，边长为6，AD⊥BC，垂足为点D，点E和点F分别是线段AD和AB上的两个动点，连接CE，EF，则CE+EF的最小值为　3　．‎ ‎【分析】过C作CF⊥AB交AD于E，则此时，CE+EF的值最小，且CE+EF的最小值＝CF，根据等边三角形的性质得到BF＝AB＝6＝3，根据勾股定理即可得到结论．‎ ‎【解答】解：过C作CF⊥AB交AD于E，‎ 则此时，CE+EF的值最小，且CE+EF的最小值＝CF，‎ ‎∵△ABC为等边三角形，边长为6，‎ ‎∴BF＝AB＝6＝3，‎ ‎∴CF＝＝＝3，‎ ‎∴CE+EF的最小值为3，‎ 故答案为：3．‎ ‎2. （2020•新疆维吾尔自治区新疆生产建设兵团•5分）如图，在△ABC中，∠A=90°，∠B=60°，AB=2，若D是BC边上的动点，则2AD+DC的最小值为_____．‎ ‎【答案】6‎ ‎【解析】‎ ‎【分析】‎ 取AC的中点F，过F作于G，延长FG至E，使EG=FG，连接AE交BC于D，则 此时最短，证明此时D为BC的中点，证明CD=2DF，从而可得答案．‎ ‎【详解】解：如图， ‎ ‎ ‎ 取AC的中点F，过F作于G，延长FG至E，使EG=FG，连接AE交BC于D，则 此时最短，‎ ‎ ‎ ‎ ‎ 过A作于H，则由 ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 为BC的中点，‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 即的最小值为6．‎ 故答案为：6．‎ ‎【点睛】本题考查的是利用轴对称求最小值问题，考查了锐角三角函数，三角形的相似的判定与性质，直角三角形的性质，勾股定理的应用，掌握以上知识是解题的关键．‎ 三.解答题 ‎1. （2020•四川省遂宁市•12分）如图，抛物线y＝ax2+bx+c（a≠0）的图象经过A（1，0），B（3，0），C（0，6）三点．‎ ‎（1）求抛物线的解析式．‎ ‎（2）抛物线的顶点M与对称轴l上的点N关于x轴对称，直线AN交抛物线于点D，直线BE交AD于点E，若直线BE将△ABD的面积分为1：2两部分，求点E的坐标．‎ ‎（3）P为抛物线上的一动点，Q为对称轴上动点，抛物线上是否存在一点P，使A.D.P、Q为顶点的四边形为平行四边形？若存在，求出点P的坐标；若不存在，请说明理由．‎ ‎【分析】（1）设抛物线解析式为：y＝a（x﹣1）（x﹣3），把点C坐标代入解析式，可求解；‎ ‎（2）先求出点M，点N坐标，利用待定系数法可求AD解析式，联立方程组可求点D坐标，可求S△ABD＝×2×6＝6，设点E（m，2m﹣2），分两种情况讨论，利用三角形面积公式可求解；‎ ‎（3）分两种情况讨论，利用平行四边形的性质可求解．‎ ‎【解答】解：（1）∵抛物线y＝ax2+bx+c（a≠0）的图象经过A（1，0），B（3，0），‎ ‎∴设抛物线解析式为：y＝a（x﹣1）（x﹣3），‎ ‎∵抛物线y＝a（x﹣1）（x﹣3）（a≠0）的图象经过点C（0，6），‎ ‎∴6＝a（0﹣1）（0﹣3），‎ ‎∴a＝2，‎ ‎∴抛物线解析式为：y＝2（x﹣1）（x﹣3）＝2x2﹣8x+6；‎ ‎（2）∵y＝2x2﹣8x+6＝2（x﹣2）2﹣2，‎ ‎∴顶点M的坐标为（2，﹣2），‎ ‎∵抛物线的顶点M与对称轴l上的点N关于x轴对称，‎ ‎∴点N（2，2），‎ 设直线AN解析式为：y＝kx+b，‎ 由题意可得：，‎ 解得：，‎ ‎∴直线AN解析式为：y＝2x﹣2，‎ 联立方程组得：，‎ 解得：，，‎ ‎∴点D（4，6），‎ ‎∴S△ABD＝×2×6＝6，‎ 设点E（m，2m﹣2），‎ ‎∵直线BE将△ABD的面积分为1：2两部分，‎ ‎∴S△ABE＝S△ABD＝2或S△ABE＝S△ABD＝4，‎ ‎∴×2×（2m﹣2）＝2或×2×（2m﹣2）＝4，‎ ‎∴m＝2或3，‎ ‎∴点E（2，2）或（3，4）；‎ ‎（3）若AD为平行四边形的边，‎ ‎∵以A.D.P、Q为顶点的四边形为平行四边形，‎ ‎∴AD＝PQ，‎ ‎∴xD﹣xA＝xP﹣xQ或xD﹣xA＝xQ﹣xP，‎ ‎∴xP＝4﹣1+2＝5或xP＝2﹣4+1＝﹣1，‎ ‎∴点P坐标为（5，16）或（﹣1，16）；‎ 若AD为平行四边形的对角线，‎ ‎∵以A.D.P、Q为顶点的四边形为平行四边形，‎ ‎∴AD与PQ互相平分，‎ ‎∴，‎ ‎∴xP＝3，‎ ‎∴点P坐标为（3，0），‎ 综上所述：当点P坐标为（5，16）或（﹣1，16）或（3，0）时，使A.D.P、Q为顶点的四边形为平行四边形．‎ ‎【点评】本题是二次函数综合题，考查了待定系数法求解析式，一次函数的性质，平行四边形的性质，利用分类讨论思想解决问题是本题的关键．‎ ‎2. （2020•四川省自贡市•14分）在平面直角坐标系中，抛物线与轴相交于、，交轴于点，点抛物线的顶点，对称轴与轴交于点. ‎ ‎⑴.求抛物线的解析式；‎ ‎⑵.如图1，连接，点是线段上方抛物线上的一动点，于点；过点作轴于点，交于点.点是轴上一动点，当取最大值时.‎ ‎①.求的最小值；‎ ‎②.如图2，点是轴上一动点，请直接写出的最小值. ‎ ‎【解析】（1）将A（-3，0）、B（1，0）代入二次函数得 解之得，∴二次函数的解析式为 ‎（2）①将二次函数配方得，∴M（-1，4）‎ 设直线AM的解析式为，将代入直线可得 解得，∴直线AM的解析式为 过E作直线，平行于直线AM，且解析式为，∵E在直线AM上方的抛物线上，‎ ‎∴；‎ 当直线与AM距离最大时，EF取得最大值，‎ ‎∴当与抛物线只有一个交点时，EF取得最大值 将直线的解析式代入抛物线得 由题意可得，△=，经计算得，将代入二次方程可得 ‎，∴，即E点的横坐标为-2，将代入抛物线得 ‎∴，又∵⊥轴，∴，将代入直线AM，∴‎ ‎∵，∴B.C两点关于轴对称，∴‎ ‎∴，当P、B.D三点不共线时 当P、B.D三点共线时，‎ ‎∴当P、B.D三点共线时PC+PD取得最小值，‎ 在Rt△BHD中。DH=2，BH=3，∴BD=‎ ‎∴的最小值为；‎ ②过Q作直线平行于轴，并在轴右侧该直线上取一点G，使得 QG=，∴，当三点共线时 DQ+QG取得最小值，设Q（0，y），则 ‎∵QG∥轴，∴，∴‎ ‎∴的最小值为 ‎3.（2020•宁夏省•10分）如图（1）放置两个全等的含有30°角的直角三角板ABC与DEF（∠B＝∠E＝30°），若将三角板ABC向右以每秒1个单位长度的速度移动（点C与点E重合时移动终止），移动过程中始终保持点B.F、C.E在同一条直线上，如图（2），AB与DF、DE分别交于点P、M，AC与DE交于点Q，其中AC＝DF＝，设三角板ABC移动时间为x秒．‎ ‎（1）在移动过程中，试用含x的代数式表示△AMQ的面积；‎ ‎（2）计算x等于多少时，两个三角板重叠部分的面积有最大值？最大值是多少？‎ ‎【分析】（1）解直角三角形ABC求得EF＝BC＝3，设CF＝x，可求，，根据三角形面积公式即可求出结论；‎ ‎（2）根据“S重叠＝S△ABC﹣S△AMQ﹣S△BPF”列出函数关系式，通过配方求解即可．‎ ‎【解答】解：（1）解：因为Rt△ABC中∠B＝30°，‎ ‎∴∠A＝60°，‎ ‎∵∠E＝30°，‎ ‎∴∠EQC＝∠AQM＝60°，‎ ‎∴△AMQ为等边三角形，‎ 过点M作MN⊥AQ，垂足为点N．‎ 在Rt△ABC中，，‎ ‎∴EF＝BC＝3，‎ 根据题意可知CF＝x，‎ ‎∴CE＝EF﹣CF＝3﹣x，‎ ‎∴，‎ ‎∴，而，‎ ‎∴，‎ ‎（2）由（1）知BF＝CE＝3﹣x，‎ ‎∴＝＝，‎ 所以当x＝2时，重叠部分面积最大，最大面积是．‎ ‎【点评】本题属于几何变换综合题，考查了平移变换，等边三角形的性质和判定，解直角三角形，二次函数的性质等知识，解题的关键是灵活运用所学知识解决问题，学会用分类讨论的思想思考问题，属于中考压轴题．‎ ‎4.（2020•广东省深圳市•9分）如图1，抛物线y=ax2+bx+3（a≠0）与x轴交于A（-3，0）和B（1，0），与y轴交于点C，顶点为D ‎（1）求解抛物线解析式 ‎（2）连接AD，CD，BC，将△OBC沿着x轴以每秒1个单位长度的速度向左平移，得到，点O、B.C的对应点分别为点，，，设平移时间为t秒，当点与点A重合时停止移动。记△与四边形AOCD的重叠部分的面积为S，请直接写出S与时间t的函数解析式;‎ ‎（3）如图2，过抛物线上任意一点M（m，n）向直线l:作垂线，垂足为E，试问在该抛物线的对称轴上是否存在一点F，使得ME-MF=？若存在，请求F点的坐标；若不存在，请说明理由。‎ 图2‎ 图1‎ ‎【考点】二次函数，变量之间的关系，存在性问题 ‎【解析】‎ 解：（1）将A（-3，0）和B（1，0）代入抛物线解析式y=ax2+bx+3中，可得：‎ ‎∴抛物线解析式为y=-x2-2x+3‎ ‎（2）①如图所示，当0

查看更多