北师大版九年级数学下册第二章测试题及答案

北师大版九年级数学下册第二章测试题及答案

北师大版九年级数学下册第二章测试题及答案 ‎(考试时间：120分钟　满分：120分)‎ 分数：____________　‎ 一、选择题(本大题共6小题，每小题3分 ，共18分，每小题只有一个正确选项)‎ ‎1．下面的函数中是二次函数的是 (　C　)‎ A．y＝3x＋1 B．y＝ C．y＝x2＋2x D．y＝ ‎2．将抛物线y＝x2－4x－4向左平移3个单位，再向上平移5个单位，得到抛物线的函数表达式为 (　D　)‎ A．y＝(x＋1)2－13 B．y＝(x－5)2－3‎ C．y＝(x－5)2－13 D．y＝(x＋1)2－3‎ ‎3．二次函数y＝ax2＋bx＋c的图象如图所示，那么一次函数y＝ax＋b的图象大致是 (　A　)‎ 第3题图 4． 若二次函数y＝|a|x2＋bx＋c的图象经过A(m，n)，B(0，y1)，C(3－m ‎，n)，D(，y2)，E(2，y3)，则y1，y2，y3的大小关系是 ‎ ‎(　D　)‎ A．y1＜y2＜y3 B．y1＜y3＜y2 C．y3＜y2＜y1 D．y2＜y3＜y1‎ ‎5．当a≤x≤a＋1时，函数y＝x2－2x＋1的最小值为1，则a的值为(　D　)‎ A．－1 B．2 C．0或2 D．－1或2‎ ‎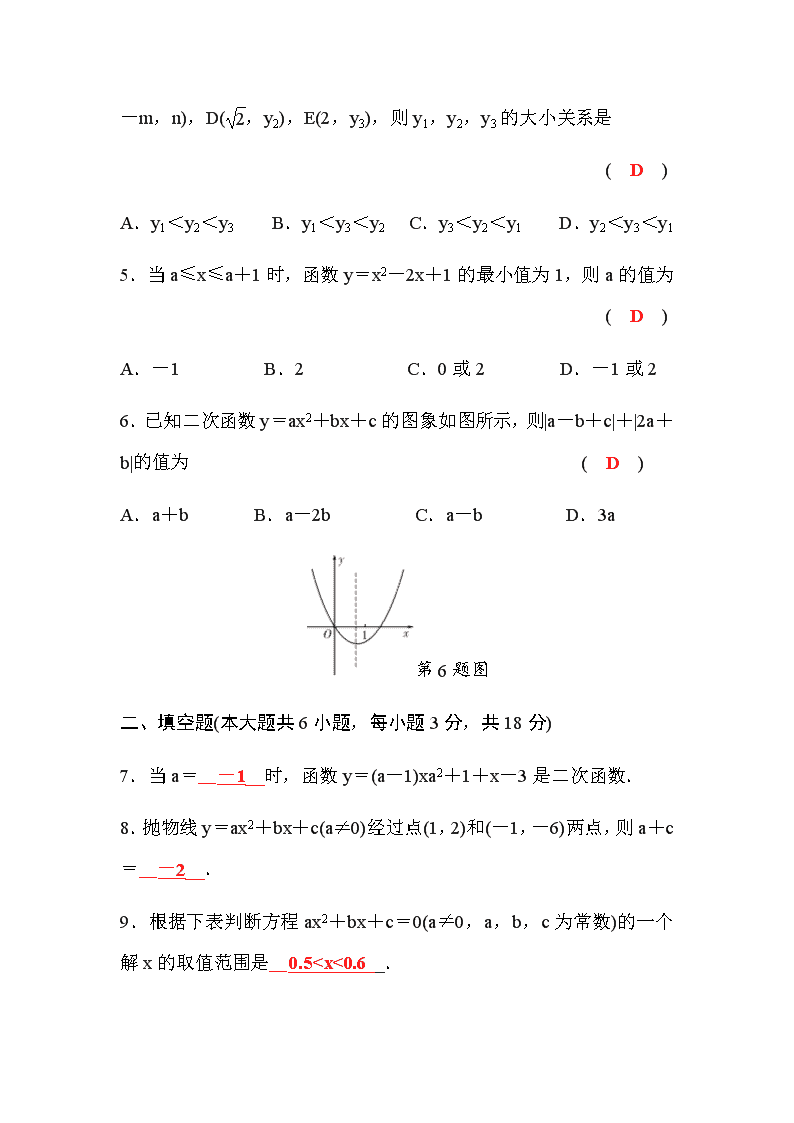6．已知二次函数y＝ax2＋bx＋c的图象如图所示，则|a－b＋c|＋|2a＋b|的值为 (　D　)‎ A．a＋b B．a－2b C．a－b D．3a ‎ 第6题图 二、填空题(本大题共6小题，每小题3分，共18分)‎ ‎7．当a＝__－1__时，函数y＝(a－1)xa2＋1＋x－3是二次函数．‎ ‎8．抛物线y＝ax2＋bx＋c(a≠0)经过点(1，2)和(－1，－6)两点，则a＋c＝__－2__．‎ ‎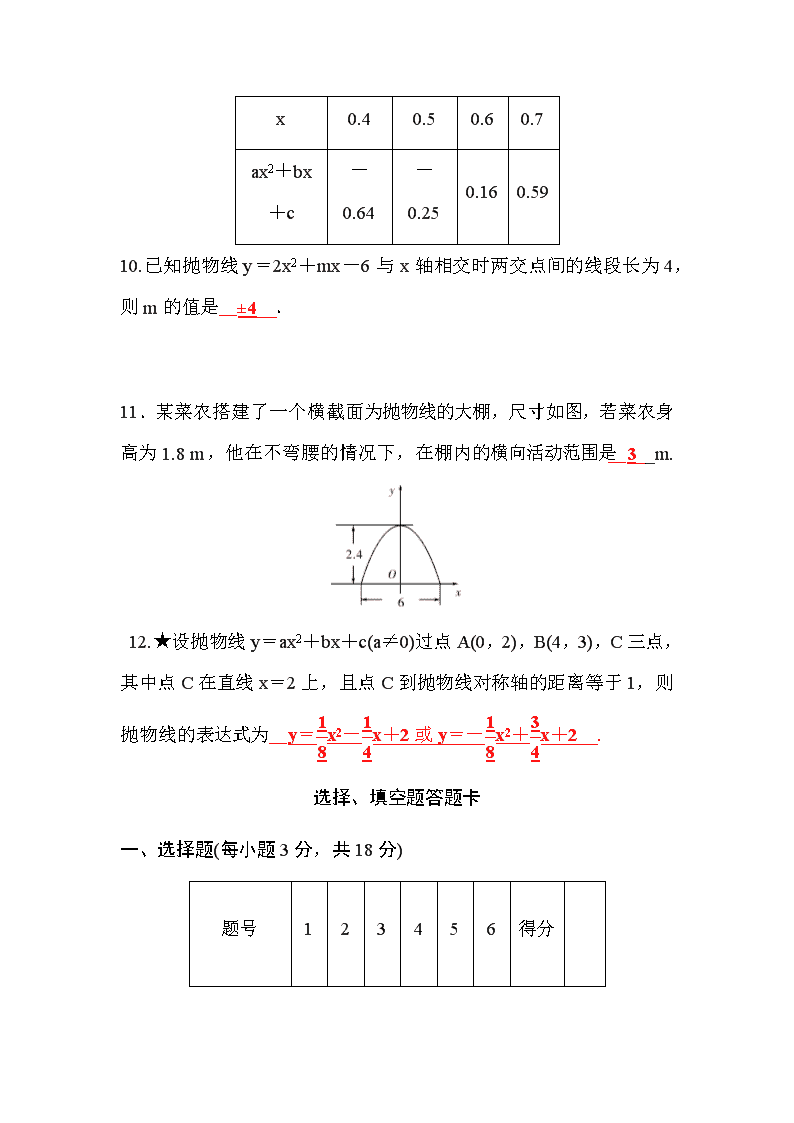9．根据下表判断方程ax2＋bx＋c＝0(a≠0，a，b，c为常数)的一个解x的取值范围是__0.50，‎ ‎∴m取任何实数时，‎ 抛物线y＝2x2－(m＋5)x＋(m＋1)与x轴必有两个交点．‎ ‎14．(玉田县期末)已知二次函数y＝a(x－1)2＋k的图象与y轴交于点C(0，－8)，与x轴的一个交点坐标是A(－2，0).‎ ‎(1)求二次函数的表达式；‎ ‎(2)当x为何值时，y＜0.‎ 解：(1)该二次函数的表达式为y＝(x－1)2－9.‎ ‎(2)由(1)可知点A(－2，0)，点B(4，0).‎ ‎∴当－2＜x＜4时，y＜0.‎ ‎15．如图，二次函数y＝(x＋2)2＋m的图象与y轴交于点C，点B在抛物线上，且与点C关于抛物线的对称轴对称，已知一次函数y＝kx＋b的图象经过该二次函数图象上的点A(－1，0)及点B.‎ ‎(1)求二次函数与一次函数的表达式；‎ ‎(2)根据图象，写出满足(x＋2)2＋m≥kx＋b的x的取值范围．‎ 解：(1)由题易得二次函数表达式为y＝x2＋4x＋3，‎ 一次函数表达式为y＝－x－1.‎ (2) 由图象可知，满足(x＋2)2＋m≥kx＋b的x的取值范围为 x≤－4或x≥－1.‎ ‎16．如图，已知二次函数y＝x2＋ax＋3的图象经过点P(－2，3).‎ ‎(1)求a的值和图象的顶点坐标；‎ ‎(2)点Q(m，n)在该二次函数图象上．‎ ‎①当m＝2时，求n的值；‎ ‎②若点Q到y轴的距离小于2，请根据图象直接写出n的取值范围.‎ 解：(1)把点P(－2，3)代入y＝x2＋ax＋3中，‎ 解得a＝2，∴y＝x2＋2x＋3＝(x＋1)2＋2，‎ ‎∴a的值是2，图象的顶点坐标为(－1，2).‎ ‎(2)①当m＝2时，n＝11；‎ ‎②点Q到y轴的距离小于2，∴|m|＜2，‎ ‎∴－2＜m＜2，∴2≤n＜11.‎ ‎∴n的取值范围是2≤n<11.‎ ‎17．(埇桥区期末)二次函数的图象经过A，C，B三点，点A的坐标为(－1，0)，点B的坐标为(4，0)，点C在y轴正半轴上，‎ 且AB＝OC，求二次函数的表达式．‎ 解：∵A(－1，0)，B(4，0)‎ ‎∴AO＝1，OB＝4，‎ AB＝AO＋OB＝1＋4＝5，‎ ‎∴OC＝5，即点C的坐标为(0，5)，‎ 设二次函数的表达式为y＝ax2＋bx＋c，‎ ‎∵二次函数的图象经过A，C，B三点，‎ ‎∴将点A(－1，0)，B(4，0)，C(0，5)代入易得二次函数的 表达式为y＝－x2＋x＋5.‎ 四、(本大题共3小题，每小题8分，共24分)‎ ‎18．如图，抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C，D两点，点P是x轴上的一个动点．‎ ‎(1)求此抛物线的表达式；‎ ‎(2)当PA＋PB值最小时，求点P的坐标．‎ 解：(1)抛物线的表达式为y＝－x2＋2x＋3.‎ ‎(2)作点B关于x轴的对称点E(0，－3)，连接AE交x轴于点P.‎ 此时PA＋PB值最小，最小值为AE的长．‎ 设AE的解析式为y＝kx＋b，‎ 则解得∴y＝7x－3.‎ ‎∵当y＝0时，x＝，‎ ‎∴点P的坐标为.‎ ‎19．如图，一座拱桥的轮廓是抛物线型，拱高6 m，在长度为8 m的两支柱OC和AB之间，还安装着三根支柱，相邻两支柱间的距离均为5 m．‎ ‎(1)建立如图所示的平面直角坐标系，求拱桥抛物线的函数表达式；‎ 解：根据题意，易得抛物线的函数表达式为y＝－x2＋x.‎ ‎(2)求支柱EF的长度；‎ ‎(3)拱桥下面拟铺设行车道，要保证高3 m的汽车能够通过(车顶与拱桥的距离不小于0.3 m)，行车道最宽可以铺设多少米？‎ 解：(2)由题意得点F的坐标为，‎ ‎∴EF＝8－＝(m)＝3.5(m).‎ ‎(3)当y＝3＋0.3＝3.3时，有 ‎－x2＋x＝3.3，化简，得x2－20x＋55＝0，‎ 解得x1＝10－3，x2＝10＋3，‎ ‎∴x2－x1＝6.‎ ‎∴行车道最宽可以铺设6 米．‎ ‎20．如图，在矩形OABC中，OA＝3，OC＝2，F是AB上的一个动点(F不与A，B重合)，过点F的反比例函数y＝(k>0)的图象与BC边交于点E.当k为何值时，△EFA的面积最大，最大面积是多少？‎ 解：由题意知E，F两点坐标分别为E，F，‎ ‎∴S△EFA＝AF·BE＝×k ‎＝k－k2‎ ‎＝－(k－3)2＋.‎ ‎∵点F在边AB上，不与A，B重合，即0<<2，‎ 解得0a，‎ ‎∴经过B，D，C的图象是y＝(a＋3)x2＋(b－15)x＋c＋18的图象．‎ ‎(2)解方程组 解得x1＝2，x2＝3，‎ ‎∴点B，D的横坐标分别为2，3.‎ ‎(3)设右边函数表达式为y＝a(x－3)2－2，‎ 把点B的坐标(2，0)代入，解得a＝2，‎ 即y＝2x2－12x＋16，‎ 因此易得左边抛物线的表达式为y＝－x2＋3x－2.‎ 六、(本大题共12分)‎ ‎23．如图，在平面直角坐标系中，已知抛物线y＝ax2＋bx－8与x轴交于A，B两点，与y轴交于点C，直线l经过坐标原点O，与抛物线的一个交点为D，与抛物线的对称轴交于点E，连接CE，已知点A，D的坐标分别为(－2，0)，(6，－8).‎ ‎(1)求抛物线的表达式，并分别求出点B和点E的坐标；‎ ‎(2)试探究抛物线上是否存在点F，使△FOE≌△FCE.若存在，请直接写出点F的坐标；若不存在，请说明理由．‎ 解：(1)抛物线的表达式为y＝x2－3x－8；‎ B(8，0)；E(3，－4).‎ ‎(2)抛物线上存在点F，使△FOE≌△FCE.‎ 由题易得OE＝CE＝5，‎ ‎∵FO＝FC，‎ ‎∴点F在OC的垂直平分线上，此时点F的纵坐标为－4，‎ ‎∴x2－3x－8＝－4，解得x＝3± ，‎ ‎∴点F的坐标为(3－，－4)或(3＋，－4).‎