正方形的性质与判定学案1

正方形的性质与判定学案1

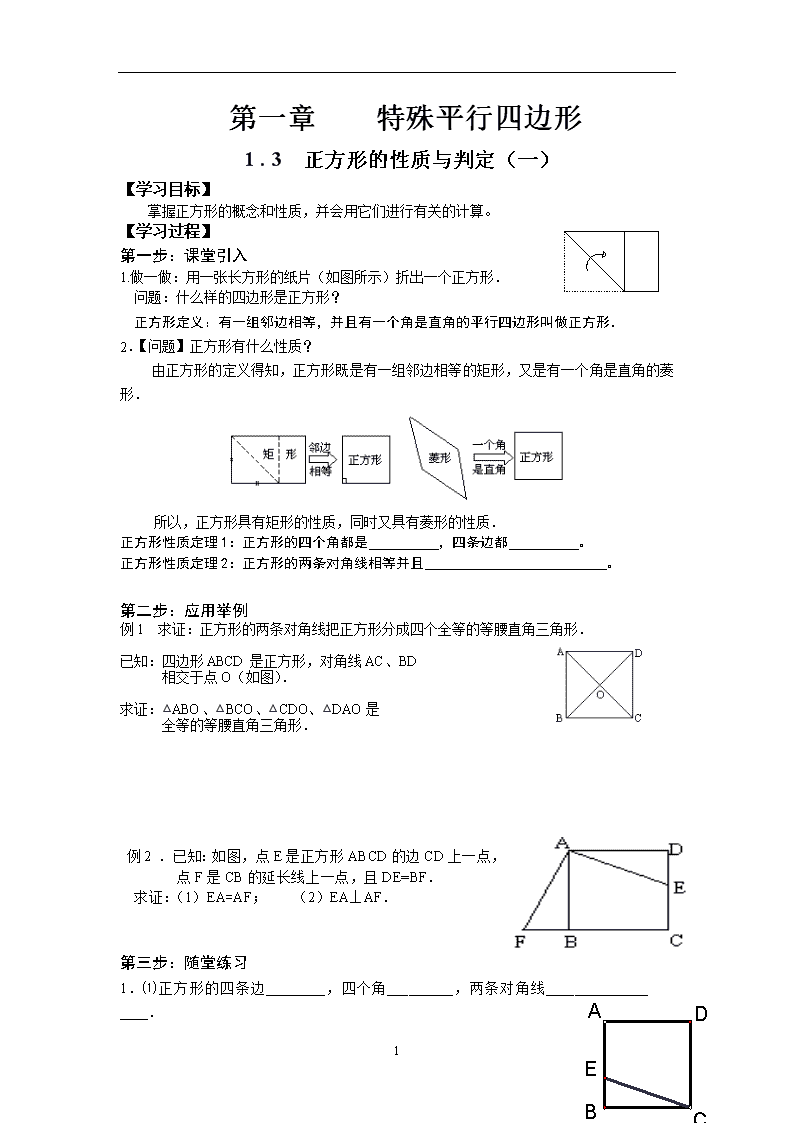
第一章 ‎ 特殊平行四边形 ‎1 . 3 正方形的性质与判定（一）‎ ‎【学习目标】‎ 掌握正方形的概念和性质，并会用它们进行有关的计算。‎ ‎【学习过程】‎ 第一步：课堂引入 ‎1.做一做：用一张长方形的纸片（如图所示）折出一个正方形．‎ 问题：什么样的四边形是正方形？‎ 正方形定义：有一组邻边相等，并且有一个角是直角的平行四边形叫做正方形．‎ ‎2．【问题】正方形有什么性质？‎ 由正方形的定义得知，正方形既是有一组邻边相等的矩形，又是有一个角是直角的菱形．‎ 所以，正方形具有矩形的性质，同时又具有菱形的性质．‎ 正方形性质定理1：正方形的四个角都是 ，四条边都 。‎ 正方形性质定理2：正方形的两条对角线相等并且 。‎ 第二步：应用举例 例1 求证：正方形的两条对角线把正方形分成四个全等的等腰直角三角形．‎ 已知：四边形ABCD是正方形，对角线AC、BD ‎ 相交于点O（如图）．‎ 求证：△ABO、△BCO、△CDO、△DAO是 全等的等腰直角三角形．‎ ‎ 例2 ．已知：如图，点E是正方形ABCD的边CD上一点，‎ 点F是CB的延长线上一点，且DE=BF．‎ 求证：（1）EA=AF； （2）EA⊥AF．‎ 第三步：随堂练习 ‎1．⑴正方形的四条边____ __，四个角___ ____，两条对角线____ _______ ____．‎ 2‎ ‎⑵正方形的两条对角线把正方形分成四个全等的__________________‎ ‎⑶正方形的边长为6，则面积为__________‎ ‎⑷正方形的对角线长为6，则面积为__________‎ ‎2．如右图，E为正方形ABCD边AB上的一点，已知EC=30, EB=10, ‎ 则正方形ABCD的面积为_______________，对角线为______ ____．‎ ‎3．如右图，E为正方形ABCD内一点，且△EBC是等边三角形，‎ 求∠EAD与∠ECD的度数．‎ 知识再现：‎ ‎ ⑴ 对边平行 边 ‎ ⑵ 四边相等 ‎ ⑶ 四个角都是直角 角 正方形 ⑷ 对角线相等 ‎ 互相垂直 对角线 ‎ 互相平分 ‎ 平分一组对角 2‎