- 2021-11-10 发布 |
- 37.5 KB |
- 6页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
江苏省无锡市华士中学2020–2021学年第一学期九年级数学第19周练习
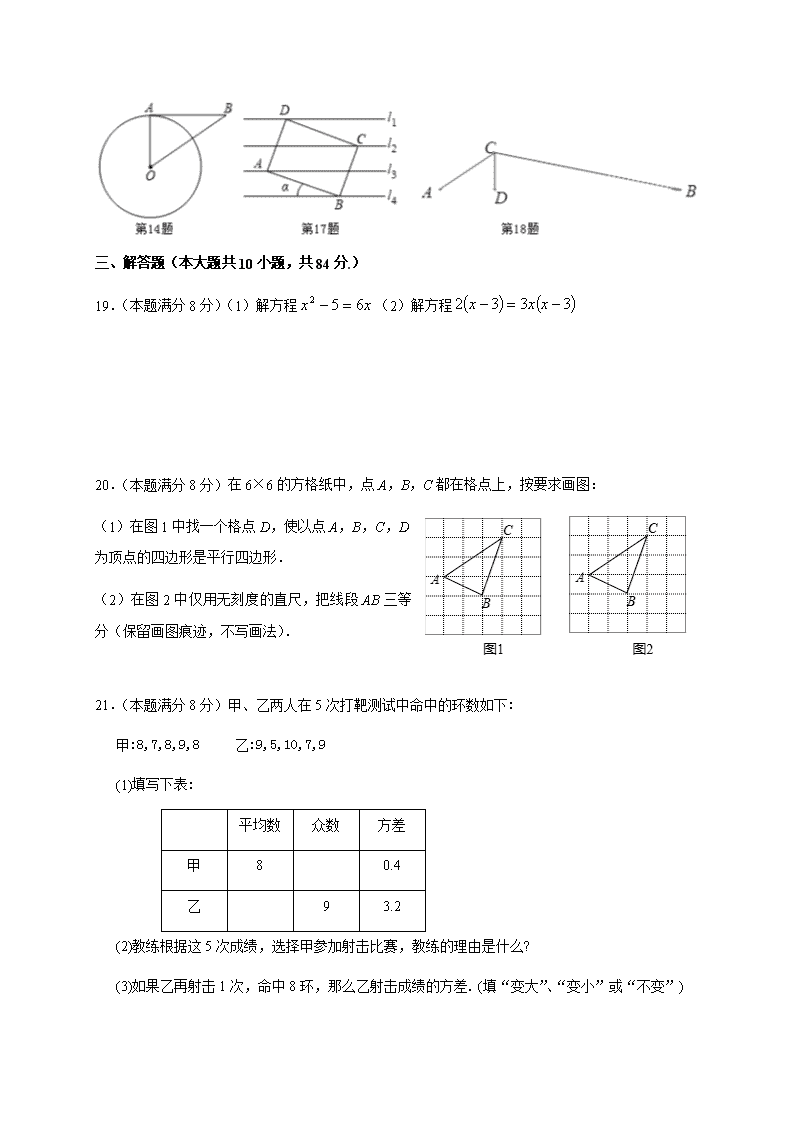
江苏省无锡市华士中学 2020–2021 学年第一学期九年级数学第 19 周练习 一、选择题(本大题共有 10 小题,每小题 3 分,共 30 分) 1.方程 x2=4 的解为() A.x=4B.x=2C.x1=4,x2=﹣4D.x1=2,x2=﹣2 2.一组数据 2,4,3,5,2 的中位数是( ) A.5 B.3.5 C.3 D.2.5 3.若△ABC∽△DEF,相似比为 1:3,则△ABC 与△DEF 的面积比为() A .1:3B.3:1C.1:9D.1: 4.把抛物线 2xy 沿 y 轴向上平移 1 个单位,所得的新抛物线的函数表达式为() A. 12 xy B. 21 xy C. 12 xy D. 21 xy 5.已知在 Rt△ABC 中,∠C=90°,BC=1,AC=2,则 tanA 的值为() A.2 B. 1 2 C. 5 5 D. 2 5 5 6.国家统计局统计数据显示,我国快递业务收入逐年增加.2017 年至 2019 年我国快递业务收入由 5000 亿元增加到 7500 亿元.设我国 2017 年至 2019 年快递业务收入的年平均增长率为 x,则可 列方程为( ) A.500(1+2x)=7500 B.5000×2(1+x)=7500 C.5000(1+x)2=7500 D.5000+5000(1+x)+5000(1+x)2=7500 7.如图,四边形 ABCD 内接于 ⊙ O,AB=CD,A 为 ��� 中点,∠BDC=60°,则∠ADB 等于( ) A.40° B.50° C.60° D.70° 8.如图,Rt△ABC 中,∠C=90°,点 D 在 AC 上,∠DBC=∠A.若 AC=4,cosA � � � ,则 BD 的 长度为( ) A.9 4 B.12 5 C.15 4 D.4 9.如图,在△ABC 中,∠A=90°,D 是 AB 的中点,过点 D 作 BC 的平行线交 AC 于点 E,作 BC 的垂线交 BC 于点 F,若 AB=CE,且△DFE 的面积为 1,则 BC 的长为( ) A.2 5 B.5 C.4 5 D.10 10.如图,点 A,B 的坐标分别为 A(2,0),B(0,2),点 C 为坐标平面内一点,BC=1,点 M 为线段 AC 的中点,连接 OM,则 OM 的最大值为( ) A. 2+11 2 B. 2+1 2 C.2 2+1 D.2 2-1 2 二、填空题(本大题共 8 小题,每小题 2 分,共 16 分.) 11.抛物线 53 2 xy 顶点坐标是. 12.已知关于 x 的方程 x2+2x+k=0 有两个相等的实数根,则 k 的值是 . 13.圆锥底面圆半径为 5,母线长为 6,则圆锥侧面积等于 .(结果保留 π ) 14.如图,AB 是 ⊙ O 的切线,A 为切点,连接 OA,OB.若∠B=35°,则∠AOB 的度数为 . 15.方程 x2+2x﹣3=0 的两根为 x1、x2,则 x1•x2 的值为 . 16.在矩形 ABCD 中,AB=6,BC=8,点 O 在对角线 AC 上,圆 O 的半径为 2,如果圆 O 与矩形 ABCD 的各边都没有公共点,那么线段 AO 长的取值范围是 . 17.如图,矩形 ABCD 的四个顶点分别在直线 l3,l4,l2,l1 上.若直线 l1∥l2∥l3∥l4 且间距相等, AB=4,BC=3,则 tan α 的值为 . 18.如图,在△ABC 中,∠ACB=135°,CD⊥AB 于 D,AD=6,BD=20,则 CD 的长度为 . 三、解答题(本大题共 10 小题,共 84 分.) 19.(本题满分 8 分)(1)解方程 xx 652 (2)解方程 3332 xxx 20.(本题满分 8 分)在 6×6 的方格纸中,点 A,B,C 都在格点上,按要求画图: (1)在图 1 中找一个格点 D,使以点 A,B,C,D 为顶点的四边形是平行四边形. (2)在图 2 中仅用无刻度的直尺,把线段 AB 三等 分(保留画图痕迹,不写画法). 21.(本题满分 8 分)甲、乙两人在 5 次打靶测试中 命中的环数如下: 甲:8,7,8,9,8 乙:9,5,10,7,9 (1)填写下表: 平均数 众数 方差 甲 8 0.4 乙 9 3.2 (2)教练根据这 5 次成绩,选择甲参加射击比赛,教练的理由是什么? (3)如果乙再射击 1 次,命中 8 环,那么乙射击成绩的方差. (填“变大”、“变小”或“不变”) 22.(本题满分 8 分)一只不透明的袋子中,装有三个大小、质地都相同的乒乓球,球面上分别标有 字母 A、O、K.搅匀后先从袋中任意摸出一个球,将对应字母记入图中的左边方格内;然后将球 放回袋中搅匀,再从袋中任意摸出一个球,将对应字母记入图中的右边方格内. (1)第一次摸到字母 A 的概率为 ; (2)用画树状图或列表等方法求两个方格中的字母从左往右恰好组成“OK”的概率. 23.(本题满分 8 分)如图,在平面直角坐标系 xOy 中,二次函数图象的顶点坐标为(4,﹣3),该 图象与 x 轴相交于点 A、B,与 y 轴相交于点 C,其中点 A 的横坐标为 1. (1)求该二次函数的表达式; (2)求 tan∠ABC. 24.(本题满分 8 分)如图,在△ABC 中,∠ACB=90°,点 D 是 BC 的中点,连接 AD,CE⊥AD 于 E,连接 BE. (1)求证:CD2=DE•DB; (2)若∠DEA=39°,求∠DAB 的度数. 25.(本题满分 8 分)某水果商店销售一种进价为 40 元/千克的优质水果,若售价为 50 元/千克,则 一个月可售出 500 千克;若售价在 50 元/千克的基础上每涨价 1 元,则月销售量就减少 10 千克. (1)当售价为 55 元/千克时,每月销售水果多少千克? (2)当月利润为 8750 元时,每千克水果售价为多少元? 26.(本题满分 8 分)如图,AB 与 ⊙ O 相切于点 B,AO 交 ⊙ O 于点 C,AO 的延长线交 ⊙ O 于点 D, E 是优弧 BCD 上不与 B,D 重合的点,sinA � � � . (1)求∠BED 的大小; (2)若 ⊙ O 的半径为 3,点 F 在 AB 的延长线上,且 BF=3 � ,求证:DF 与 ⊙ O 相切. 27.(本题满分 10 分)如图 1,点 B 在线段 CE 上,Rt△ABC≌Rt△CEF,∠ABC=∠CEF=90°, ∠BAC=30°,BC=1. (1)点 F 到直线 CA 的距离是 ; (2)固定△ABC,将△CEF 绕点 C 按顺时针方向旋转 30°,使得 CF 与 CA 重合,并停止旋转. ① 请你在图 1 中用直尺和圆规画出线段 EF 经旋转运动所形成的平面图形(用阴影表示,保留画 图痕迹,不要求写画法).该图形的面积为 ; ② 如图 2,在旋转过程中,线段 CF 与 AB 交于点 O,当 OE=OB 时,求 OF 的长. 28.(本题满分 10 分)如图,在矩形 ABCD 中,AB=4cm,BC=10cm,点 P 从点 A 出发,以 1cm/s 的速度沿射线 AB 方向匀速移动.连接 PD、AC 相交于点 E,过点 A 作 AF⊥PD,垂足为点 F.设 运动时间为 t(s). (1)当点 F 为 PD 中点时,t=_________; (2)当点 F 落在边 BC 上时,求 t 的值; (3)当△PAE 为等腰三角形时,直接写出 t 的值.查看更多