九年级上册青岛版数学教案3-4直线与圆的位置关系（3）

九年级上册青岛版数学教案3-4直线与圆的位置关系（3）

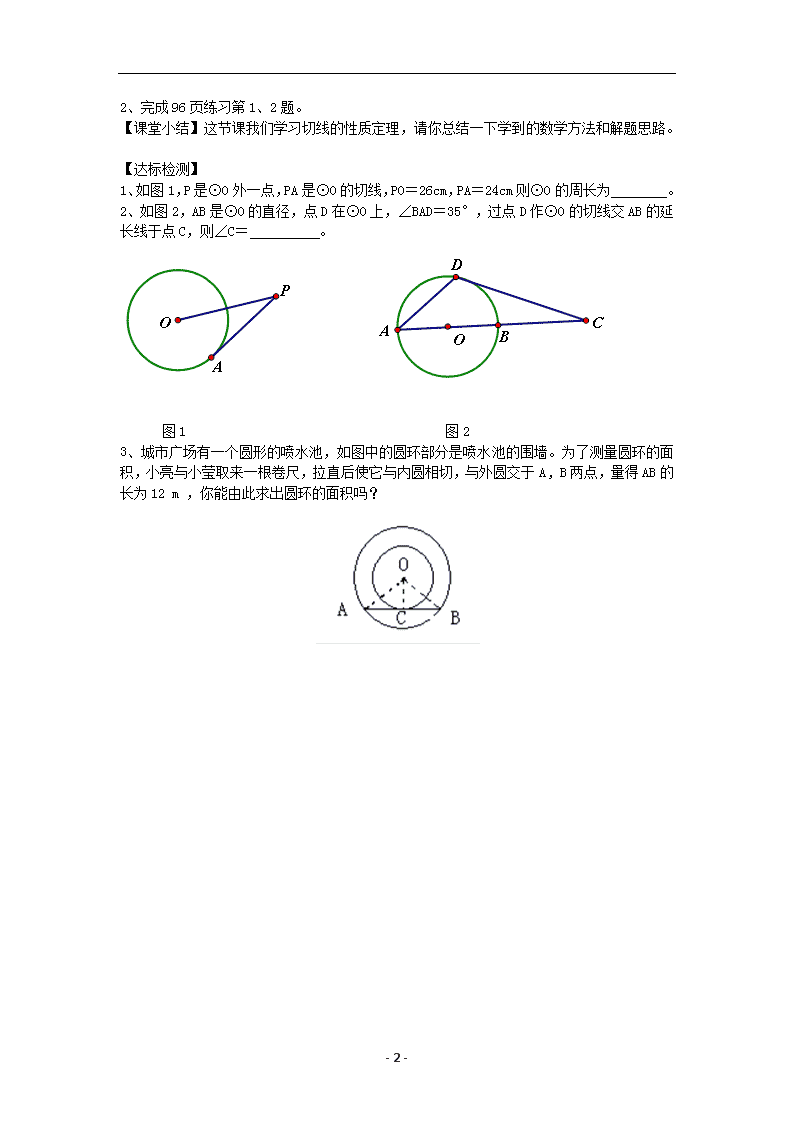
- 1 - 3.4 直线与圆的位置关系（3） 教学目标 【知识与能力】 1.掌握切线的性质定理. 2.能运用切线的性质定理进行证明和计算. 【过程与方法】 能运用切线的性质定理解决问题． 【情感态度价值观】 提高逻辑推理能力． 教学重难点 【教学重点】 切线的性质定理的应用． 【教学难点】 切线的性质定理的应用． 课前准备 多媒体课件 教学过程 1.用反证法证明的一般步骤是什么？ 2.说出证明一条直线是不是圆的切线的两种解题思路。 3.已知如图， AB＝AC，以 AB 为直径的⊙O 交 BC 于点 D，过点 D 作 DE⊥AC 于点 E，求证 DE 是⊙O 的切线。 【创设情境】 上节课我们学习了切线的判定定理，我们继续学习切线的性质。 【探索新知】 1、思考交流：你能说出切线的判定定理的逆命题吗？这个逆命题是真命题还是假命题？ 2、证明结论：在下面的空白处画出图形，写出已知和求证，用反证法证明一下。 3、由此得到：切线的性质定理： 。 【巩固提升】 1、学习课本 95 页例 3，学生独立思考后，师生共同规范步骤并总结方法。 方法总结： 在解决有关圆的切线问题时，常常需要作出过切点的半径。 - 2 - 2、完成 96 页练习第 1、2 题。 【课堂小结】这节课我们学习切线的性质定理，请你总结一下学到的数学方法和解题思路。 【达标检测】 1、如图 1，P 是⊙O 外一点，PA 是⊙O 的切线，PO＝26cm，PA＝24cm 则⊙O 的周长为 。 2、如图 2，AB 是⊙O 的直径，点 D 在⊙O 上，∠BAD＝35°，过点 D 作⊙O 的切线交 AB 的延 长线于点 C，则∠C＝ 。 图 1 图 2 3、城市广场有一个圆形的喷水池，如图中的圆环部分是喷水池的围墙。为了测量圆环的面 积，小亮与小莹取来一根卷尺，拉直后使它与内圆相切，与外圆交于 A , B 两点，量得 AB 的 长为 12 m ，你能由此求出圆环的面积吗？