- 2021-11-06 发布 |
- 37.5 KB |
- 9页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2013年贵州省贵阳市中考数学试题(含答案)
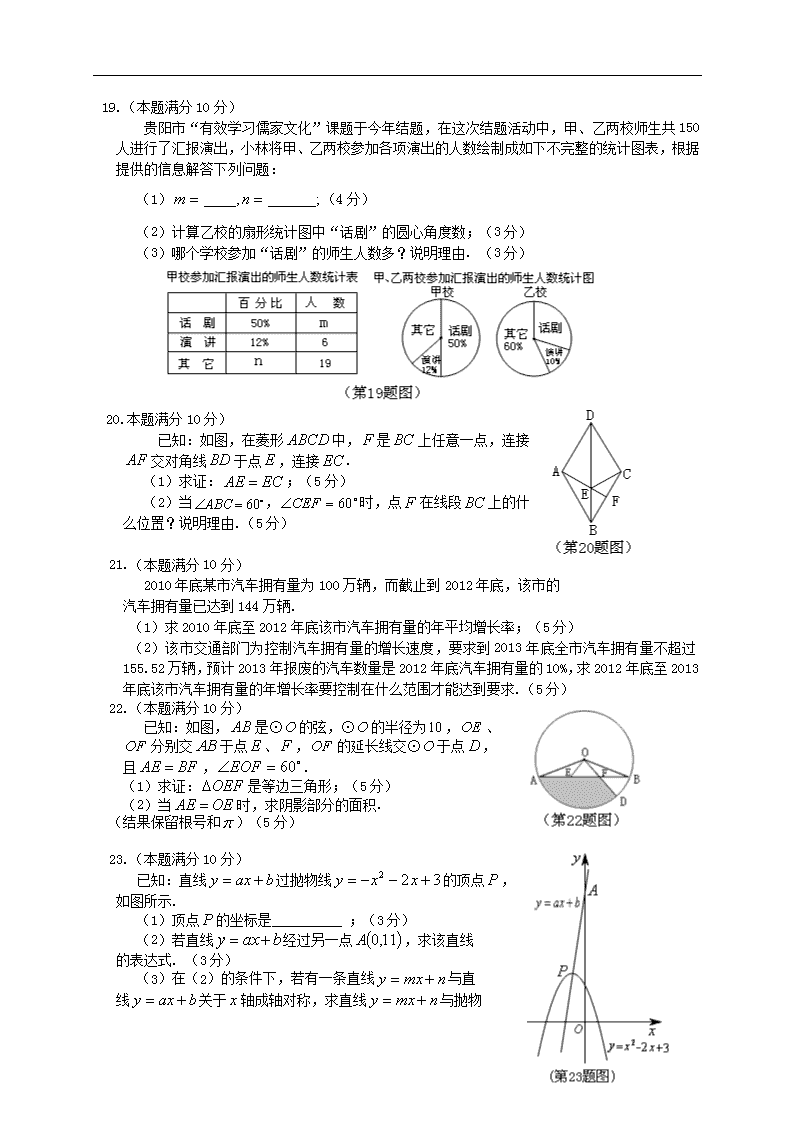
2013贵阳市年初中毕业生学业考试试题 数 学 考生注意: 1.本卷为数学试题卷,全卷共4页,三大题25小题,满分150分.考试时间为120分钟. 2.一律在《答题卡》相应位置作答,在试题卷上答题视为无效. 3.可以使用科学计算器. 一、选择题(以下每小题均有A、B、C、D四个选项,其中只有一个选项正确,请用2B铅笔在《答题卡》上填涂正确选项的字母框,每小题3分,共30分) 1. 3的倒数是( ) (A) (B) (C) (D) 2. 2013年5月在贵阳召开的“第十五届中国科协年会”中,贵州省签下总金额达790亿元的项目,790亿元用科学记数法表示为( ) (A)亿元 (B)亿元 (C)亿元 (D)亿元 3.如图,将直线沿着的方向平移得到直线,若, 则的度数是( ) (A) (B) (C) (D) 4.在端午节到来之前,儿童福利院对全体小朋友爱吃哪几种粽子作调查,以决定最终买哪种粽子.下面的调查数据中最值得关注的是( ) (A)方差 (B)平均数 (C)中位数 (D)众数 5.一个几何体的三视图如图所示,则这个几何体的位置是( ) 6.某校学生小亮每天骑自行车上学时都要经过一个十字路口,设十字路口有红、黄、绿三色交通信号灯,他在路口遇到红灯的概率为,遇到绿灯的概率为,那么他遇到黄灯的概率为( ) (A) (B) (C) (D) 7.如图,P是的边OA上一点,点P的坐标为,则 等于( ) (A) (B) (C) (D) 8.如图,是的斜边上异于、的一定点,过 点作直线截,使截得的三角形与相似,这样的直线 共有( ) (A)1条 (B)2条 (C)3条 (D)4条 9.如图,在直径为的半圆上有一动点从点出发,按顺时针方向绕半圆匀速运动到点,然后再以相同的速度沿着直径回到点停止,线段的长度与运动时间之间的函数关系用图象描述大致是( ) 10.在矩形中,,,有一个半径为1的硬 币与边、相切,硬币从如图所示的位置开始,在矩形内 沿着边、、、滚动到开始的位置为止,硬币自 身滚动的圈数大约是( ) (A)1圈 (B)2圈 (C)3圈 (D)4圈 二、填空题(每小题4分,共20分) 11.方程的解是 . 12.在一个不透明的袋子中有10个除颜色外均相同的小球,通过 多次摸球实验后,发现摸到白球的频率约为40%,估计袋中白 球有 个. 13.如图,、分别是直径和弦,,是 上一点,,垂足为,,则 等于 . 14.直线与双曲线相交于,两点,则 的值为 . 15.已知二次函数,当时,的值随值的增大而增大,则实数 的取值范围是 . 三、解答题: 16.(本题满分6分)先化简,再求值:,其中. 17.(本题满分10分) 现有两组相同的扑克牌,每组两张,两张牌的牌面数字分别是2和3,从每组牌中各随机摸出一张牌,称为一次试验. (1)小红与小明用一次试验做游戏,如果摸到的牌面数字相同小红获胜,否则小明获胜,请用列表法或画树状图的方法说明这个游戏是否公平?(5分) (2)小丽认为:“在一次试验中,两张牌的牌面数字和可能为4、5、6三种情况,所以出现‘和为4’的概率是”,她的这种看法是否正确?说明理由.(5分) 18.(本题满分10分) 在一次综合实践活动中,小明要测某地一座古塔的高度,如图,已知塔基的高为,他在处测得塔基顶端的仰角为,然后沿方向走到达点,又测得塔顶的仰角为.(人的身高忽略不计) (1)求的距离;(结果保留根号)(5分) (2)求塔高.(结果保留整数)(5分) 19.(本题满分10分) 贵阳市“有效学习儒家文化”课题于今年结题,在这次结题活动中,甲、乙两校师生共150人进行了汇报演出,小林将甲、乙两校参加各项演出的人数绘制成如下不完整的统计图表,根据提供的信息解答下列问题: (1)(4分) (2)计算乙校的扇形统计图中“话剧”的圆心角度数;(3分) (3)哪个学校参加“话剧”的师生人数多?说明理由. (3分) 20.本题满分10分) 已知:如图,在菱形中,是上任意一点,连接 交对角线于点,连接. (1)求证:;(5分) (2)当,时,点在线段上的什 么位置?说明理由.(5分) 21.(本题满分10分) 2010年底某市汽车拥有量为100万辆,而截止到2012年底,该市的 汽车拥有量已达到144万辆. (1)求2010年底至2012年底该市汽车拥有量的年平均增长率;(5分) (2)该市交通部门为控制汽车拥有量的增长速度,要求到2013年底全市汽车拥有量不超过155.52万辆,预计2013年报废的汽车数量是2012年底汽车拥有量的10%,求2012年底至2013年底该市汽车拥有量的年增长率要控制在什么范围才能达到要求.(5分) 22.(本题满分10分) 已知:如图,是⊙的弦,⊙的半径为,、 分别交于点、,的延长线交⊙于点, 且,. (1)求证:是等边三角形;(5分) (2)当时,求阴影部分的面积. (结果保留根号和)(5分) 23.(本题满分10分) 已知:直线过抛物线的顶点, 如图所示. (1)顶点的坐标是 ;(3分) (2)若直线经过另一点,求该直线 的表达式. (3分) (3)在(2)的条件下,若有一条直线与直 线关于轴成轴对称,求直线与抛物 线的交点坐标. (4分) 24.(本题满分12分) 在中,,,,设为最长边,当时,是直角三角形;当时,利用代数式和的大小关系,探究的形状(按角分类). (1)当三边分别为6、8、9时,为 三角形;当三边分别为6、8、11时,为 三角形.(4分) (2)猜想,当 时,为锐角三角形;当 时,为钝角三角形. (4分) (3)判断当,时,的形状,并求出对应的的取值范围.(4分) 25.(本题满分12分) 如图,在平面直角坐标系中,有一条直线:与轴、轴分别交于点、,一个高为3的等边三角形,边在轴上,将此三角形沿着轴的正方向平移. (1)在平移过程中,得到,此时顶点恰 落在直线上,写出点的坐标 ;(4分) (2)继续向右平移,得到,此时它的外心 恰好落在直线上,求点的坐标;(4分) (3)在直线上是否存在这样的点,与(2)中的、 、任意两点能同时构成三个等腰三角形,如果存在, 求出点的坐标;如果不存在,说明理由. (4分) 2013年贵阳市初中毕业生学业考试试题 数学参考答案及评分标准 一、选择题(每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案 D B B D A D C C A B 二、填空题(每小题4分,共20分) 题 号 11 12 13 14 15 答 案 三、解答题: 16.(本题满分6分) 解: 原式 ……………………………………3分 ……………………………………5分 当时,原式 ……………………………………6分 17.(本题满分10分) 解:(1)列表正确或画树状图正确给2分 ……………………………………3分 ……………………………………4分 ∵ ∴这个游戏公平.……………………………………5分 (2)不正确. ……………………………………6分 因为“和为4”只出现了一次,由列表或树状图可知和的情况总共有4种. 故“和为4”的概率为. ……………………………………10分 18.(本题满分10分) 解:(1)在中, , ∴ ……………………………………2分 ∴ 答:的距离为. ……………………………………5分 (2)在中, ,………………………6分 ∴ ……………………………………8分 ∴ 答:塔高约. ……………………………………10分 19.(本题满分10分) 解:(1) 25 ; 38% . ……………………………………4分 (2) ∴圆心角为. ……………………………………7分 (3)(人) ……………………………………9分 ∵ ∴乙校参加“话剧”的师生人数多.…………………10分 20.(本题满分10分) 解:(1)证明:连接 …………………………………1分 ∵是菱形的对角线,垂直平分. ……………………3分 ∴ ………………………………5分 (2)答:点是线段的中点. ………………………………6分 理由:∵菱形中,,又 ∴是等边三角形, …………………………7分 ∵ ∴ ………………8分 ∴是的平分线 ………………………………9分 ∵交于点,∴是的边上的中线. ∴点是线段的中点. ………………………………10分 21.(本题满分10分) 解(1)设2010年底至2012年底该市汽车拥有量的年平均增长率为. ………1分 由题意得: ………………………………3分 解得:,(不合题意,舍去) 答:2010年底至2012年底,该市汽车拥有量的年平均增长率为20%.……5分 (2)设2012年底至2013年底该市汽车拥有量的年平均增长率为. 由题意得: ………………………………8分 解得: ………………………………9分 答:2012年底至2013年底该市汽车拥有量的年平均增长率不超过18%才能达到要求. ………………………………10分 22.(本题满分10分) (1)证明:作于点 …………………1分 ∴ …………………2分 ∵ ∴ ………………3分 ∵ ∴ ………………4分 ∵ ∴是等边三角形.…………5分 (2)解:∵在等边三角形中,, 又 ∴, ∴ ………………………………6分 ∵ ∴ ………………………………7分 ………………………………8分 ………………………………9分 ∴ ………………………………10分 23.(本题满分10分) 解(1) ………………………………3分 (2)将点,代入得 …………4分 解得 ………………………………5分 ∴这条直线的表达式为. ………………………………6分 (3)∵直线与直线关于轴成轴对称. ∴过点、 ……………………………7分 解得 ∴……………8分 ………………………………9分 解得 ,此时 ∴直线与抛物线的交点坐标为,…10分 24.(本题满分12分) 解(1)锐角,钝角 ………………………………4分 (2), ………………………………8分 (3)∵为最长边 ∴ ………………………………9分 ① ,即, ∴当时,这个三角形是锐角三角形.………………………10分 ②, , ∴当时,这个三角形是直角三角形. ………………………11分 ③,, ∴当时,这个三角形是钝角三角形.………………………12分 25.(本题满分12分) (1) ………………………………4分 (2)设,连接并延长交轴于点,连接 ………………………5分 在等边三角形中,高 ∴, ………………………………6分 ∵点是等边三角形的外心 ∴,∴ 即 ………………………………7分 将代人,解得: ∴ ………………………………8分 (3)点是的外心,∵ ,,是等腰三角形 ∴点满足条件,由(2)得 ………………………………9分 由(2)得:,点满足直线:的关系式. ∴点与点重合. ∴ 设点满足条件,,, 能构成等腰三角形. 此时 作轴于点,连接 ∵, ∴,∴ ………………………………10分 设点满足条件,,,能构成等腰三角形. 此时 作轴于点 ∵, ∴ ∴ ………………………………11分 设点满足条件,,,能构成等腰三角形. 此时 作轴于点 ∵, ∴ ∴ 答:存在四个点,分别是,,, ………………………………………………………………12分查看更多