2020年苏科版九年级下册第六章《图形的相似》（基础题）单元测试（二）

2020年苏科版九年级下册第六章《图形的相似》（基础题）单元测试（二）

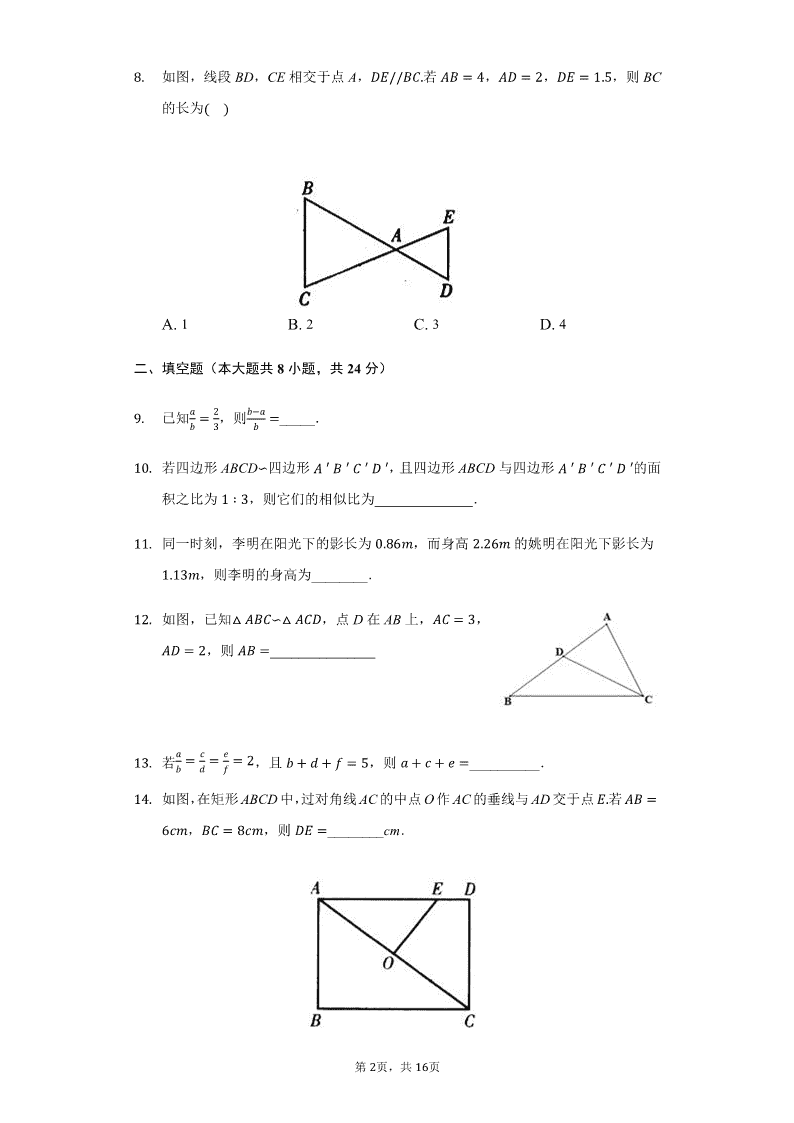
2020苏科版九下第六章《图形的相似》（基础题）单元测试（二）班级：___________姓名：___________得分：___________一、选择题（本大题共8小题，共24分）1.两个相似五边形的相似比为2：3，则它们的面积比为A.2：3B.3：2C.4：9D.9：4ݔݔ2.小明由等积式ݔ6写了以下比例式：；；；，ݔ666ݔ6则小明写出的比例式中正确的是．A.B.C.D.3.下列长度的各组线段中，是成比例线段的是A.2，5，6，8B.3，6，9，18C.1，2，3，4D.3，6，7，94.已知线段3͵，12͵，线段c是a，b的比的中项，则c等于A.4cmB.6cmC.8cmD.10cm.已知香䁨th，香䁨的面积为1，th的面积为4，则香䁨与th的周长之比为A.1香2B.1香4C.2香1D.4香16.用x、2、6和12这四个数组成比例，x不可能是A.1B.3C.4D.367.要制作两个形状相同的三角形框架，其中一个三角形的边长分别为㎝，6㎝和㎝，另一个三角形的最短边长为2.㎝，则它的最长边为．A.3㎝B.4㎝C.4.㎝D.㎝第1页，共16页 8.如图，线段BD，CE相交于点A，t香䁨.若香4，2，t1.，则BC的长为A.1B.2C.3D.4二、填空题（本大题共8小题，共24分）2.已知，则_____．310.若四边形ABCD四边形쳌香쳌䁨쳌쳌，且四边形ABCD与四边形쳌香쳌䁨쳌쳌的面积之比为13，则它们的相似比为______________．11.同一时刻，李明在阳光下的影长为0.86，而身高2.26的姚明在阳光下影长为1.13，则李明的身高为________．12.如图，已知香䁨䁨，点D在AB上，䁨3，2，则香_______________͵13.若2，且൅൅，则൅͵൅__________．14.如图，在矩形ABCD中，过对角线AC的中点O作AC的垂线与AD交于点t.若香6͵，香䁨8͵，则t________cm．第2页，共16页 1.如图是测量河宽的示意图，AE与BC相交于点D，香䁨0，测得香120，䁨60，t䁨0，求得河宽香_________m．16.如图，直线123，直线AC分别交1、2、3于点A、B、C；过点B的直线DE分别交1、3于点D、t.若香2，香䁨4，香1.，则线段DE的长为_____．三、解答题（本大题共9小题，共102分）17.如图，在香䁨中，t香䁨，h香，求证：t䁨h．18.如图，在香䁨中，香8，香䁨4，䁨6，䁨香，BD是香䁨的平分线，BD交AC于点E，求AE的长．第3页，共16页 1.将边长为4的等边香䁨的边BC向两端延长，使120.求证：香䁨；20.如图，的弦AB和CD交于点P，求证：香䁨.21.如图，在香䁨中，香䁨，香䁨，垂足为D，点E是AD上一点，连结EB，EC．第4页，共16页 1求证：t香t䁨．2若t䁨䁨，香䁨8，求DE的长．22.如图，香䁨的点A，C在上，与AB相交于点D，连接CD，30，䁨2．1求圆心O到弦DC的距离；2若䁨香൅䁨180，求证：BC是的切线．第页，共16页 23.如图，在香䁨中，香䁨，以AC为直径作交BC与点D，过点D作的切线EF，交AB于点E，交AC的延长线于点F．1求证：香䁨；2求证：香䁨2h䁨；3若3，h7，求CF的长．24.某一天，小明和小亮来到一河边，想用遮阳帽和皮尺来测量这一条河流的大致宽度，两人在确保无安全隐患的情况下，现在河岸边选择了一点香点B与河对岸岸边上的一棵树的底部点D所确定的直线垂直于河岸小明在B点面向树的方向站好，调整帽檐，使视线通过帽檐正好落在树的底部点D处，如图所示，这时小亮测得小明眼睛距地面的距离香1.7米；小明站在原地转动后蹲下，并保持原来的观察姿态除身体重心下移外，其第6页，共16页 他姿态均不变，这时视线通过帽檐落在了DB延长线上的点E处，此时小亮测得香t.6米，小明的眼睛距离地面的距离䁨香1.2米。根据以上测量过程及测量数据，请你求出河宽BD是多少米？25.如图，在香䁨中，香0，香䁨香，在BC边上取点D，使香香，构造正方形ABDE，DE交AC于点F，作t䁨交AC于点G，BC于点H．1求证：th≌t䁨．2若香3，䁨2h，求BC的长．第7页，共16页 答案和解析1.C解：两个相似五边形的相似比为2：3，两个相似五边形的面积比为4：9．2.A解：，ݔ6，故正确；ݔ6ݔ，6ݔ，故错误；6ݔ，ݔ6，故正确；6，ݔ30，故错误；ݔ63.B解：.628，故本选项错误；B.3186，故本选项正确；C.1423，故本选项错误；D.367，故本选项错误．4.B解：线段3͵，12͵，线段c是a，b的比的中项，͵3͵，将3͵，12͵代入得，，͵͵12解得：͵6͵，第8页，共16页 5.A解：因为香䁨th，所以香䁨的面积与th的面积比是香䁨与th的周长之比的平方，而香䁨的面积为1，th的面积为4，即面积比为1：4，所以香䁨与th的周长之比1香2．6.B解：.当ݔ1时，11226，1、12、2、6这四个数能组成比例，不符合题意；B.当ݔ3时，两个内项的积不等于两个外项的积，3、2、6、12这四个数不能组成比例，符合题意；C.当ݔ4时，46212，4、6、2、12这四个数能组成比例，不符合题意；D.当ݔ36时，236612，2、6、12、36这四个数能组成比例，不符合题意．7.C解：设另一个三角形的最长边长为xcm，根据题意，得：，2.ݔ解得：ݔ4.，即另一个三角形的最长边长为4.͵，8.C解：t香䁨，香4，2，t1.，t，香香䁨21.即，4香䁨解得：香䁨3，第页，共16页 19.32解：由，设2ݔ，3ݔ，33ݔ2ݔ1把2ݔ，3ݔ代入．3ݔ310.13解：四边形ABCD四边形쳌香쳌䁨쳌쳌，且四边形ABCD与四边形쳌香쳌䁨쳌쳌的面积之比为13，它们的相似比为13．11.1.72解：光线是平行的，影长都在地面上，光线和影长组成的角相等；姚明和李明与影长构成的角均为直角，李明与影长构成的三角形和姚明和影长构成的三角形相似，设李明的身高为xm，ݔ0.86，2.261.13解得ݔ1.72．12.4.解：香䁨䁨，点D在AB上，䁨3，2，香䁨，䁨第10页，共16页 香3，32解得：香4.．13.10͵解：2，2，͵2，2，൅͵൅2൅൅，൅൅，൅͵൅210．14.1.7．四边形ABCD是矩形，香6͵，香䁨8͵，香䁨，䁨香2൅香䁨262൅8210，11䁨䁨10，t香䁨，22t䁨，t香䁨0，t䁨香，t1，t香6，香䁨香䁨香8422൅t2212在t中，t൅，421t2൅6.2，4tt86.21.7͵．15.100解：香t䁨，香䁨t䁨0，香t䁨，香香，t䁨䁨第11页，共16页 香t䁨香䁨1200解得：香100米．6016.4.解：123香香，香䁨香t21.即，4香t香t3，t3൅1.4.．17.证明：t香䁨，h香，t䁨，h䁨香，t香，th䁨，t䁨h．18.解：香是香䁨的平分线，香䁨香，䁨香，香，䁨香，䁨香䁨4，又䁨香，香t䁨t，䁨t䁨41，t香82䁨t൅t䁨6，t4.19.解：൅൅180，120，香൅䁨60，第12页，共16页 又香൅香香䁨60，香䁨，同理香䁨，香䁨；20.证明：连接AC、BD，如图所示：，䁨香、䁨香所对应圆弧都为弧BC，䁨香䁨香，䁨香，䁨香，，䁨香香䁨．21.1证明：香䁨，香䁨是等腰三角形，又香䁨，香䁨，垂直平分BC，tt䁨．12解：由1可知，香䁨，香䁨84，2䁨0，又t䁨䁨，䁨䁨t，t䁨t4，即，䁨48第13页，共16页 t2．22.解：1连接OD，OC，过O作t䁨于E，30，䁨60，䁨，䁨2，䁨是等边三角形，䁨䁨2，t䁨，2t，t0，t30，26t3t，26圆心O到弦DC的距离为：．22由1得，䁨是等边三角形，䁨60，䁨香൅䁨180，䁨香൅䁨180，䁨香䁨香，香香，䁨香䁨香，香䁨30，䁨香0，香䁨是的切线23.1证明：连接AD，䁨是直径，第14页，共16页 䁨0，香䁨香䁨，香䁨；12证明：连接OD，由等腰三角形三线合一可得䁨香䁨2th是圆O的切线，th，h0，h䁨൅䁨0又䁨൅䁨0，䁨，䁨䁨1h䁨䁨香䁨2即香䁨2h䁨；3解：h䁨h，h䁨h，h䁨h，䁨hh2，h䁨hh，hh72䁨h䁨h൅6，解得䁨h1舍去负值．24.解：由题意得，香香䁨t，香䁨香t0，香香䁨t，香香，香t䁨香香1.7，.61.2解得香13.6．答：河宽BD是13.6米．25.解：1证明：正方形ABDE，tt，t൅t䁨0，th，t൅th0，tht䁨，第1页，共16页 tht䁨0，th≌t䁨；2th≌t䁨，th䁨，䁨2h，th2h，䁨t，䁨hth，䁨h1，tth23䁨，23香䁨香൅䁨3൅．22第16页，共16页