- 2021-11-06 发布 |
- 37.5 KB |
- 7页


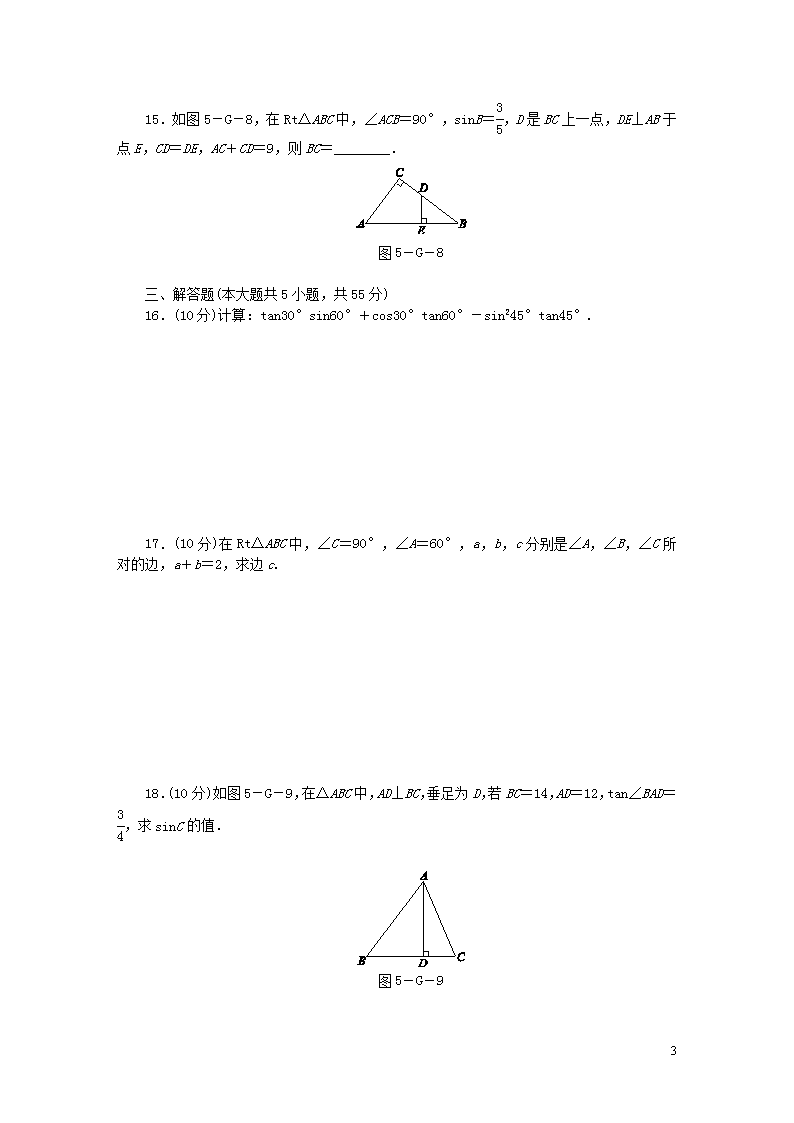
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020年秋九年级数学上册 第4章 锐角三角函数
4.1~4.3 一、选择题(本大题共8小题,每小题3分,共24分) 图5-G-1 1.如图5-G-1,在Rt△ABC中,∠C=90°,AB=5,AC=2,则cosA的值是( ) A. B. C. D. 2.如图5-G-2,在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,则下列结论中不正确的是( ) A.sinB= B.sinB= C.sinB= D.sinB= 图5-G-2 图5-G-3 3.如图5-G-3,△ABC的顶点是正方形网格的格点,则sinA的值为( ) A. B. C. D. 4.在Rt△ABC中,cosA=,则sinA的值是( ) A. B. C. D. 5.计算cos245°+sin245°的结果是( ) A. B.1 C. D. 6.当锐角A>45°时,sinA的值( ) A.小于 B.大于 7 C.小于 D.大于 7.在△ABC中,∠A,∠B为不相等的锐角,且sinA=cosB,则这个三角形是( ) A.等腰三角形 B.锐角三角形 C.钝角三角形 D.直角三角形 8.在△ABC中,AB=12 ,AC=13,cosB=,则BC边的长为( ) A.7 B.8 C.8或17 D.7或17 二、填空题(本大题共7小题,每小题3分,共21分) 9.计算:sin60°-tan30°=________. 10.如图5-G-4,在△ABC中,∠C=90°,AB=5,BC=3,则cosA的值是________. 图5-G-4 图5-G-5 11.如图5-G-5,将∠AOB放在边长为1的小正方形组成的网格中,则tan∠AOB=________. 12.在△ABC中,∠A,∠B均为锐角,若+|-sinB|=0,则∠C=________°. 13.如图5-G-6,在菱形ABCD中,DE⊥AB于点E,DE=6 cm,sinA=,则菱形ABCD的面积是________ cm2. 图5-G-6 图5-G-7 14.如图5-G-7所示,△ABC的三个顶点分别在边长为1的正方形网格的格点上,则tan(α+β)________tanα+tanβ.(填“>”“=”或“<”) 7 15.如图5-G-8,在Rt△ABC中,∠ACB=90°,sinB=,D是BC上一点,DE⊥AB于点E,CD=DE,AC+CD=9,则BC=________. 图5-G-8 三、解答题(本大题共5小题,共55分) 16.(10分)计算:tan30°sin60°+cos30°tan60°-sin245°tan45°. 17.(10分)在Rt△ABC中,∠C=90°,∠A=60°,a,b,c分别是∠A,∠B,∠C所对的边,a+b=2,求边c. 18.(10分)如图5-G-9,在△ABC中,AD⊥BC,垂足为D,若BC=14,AD=12,tan∠BAD=,求sinC的值. 图5-G-9 7 19.(12分)已知两角和的正切公式是tan(α+β)=,试求tan75°的值. 20.(13分)如图5-G-10,△ABC中,∠ACB=90°,sinA=,BC=8,D是AB的中点,过点B作直线CD的垂线,垂足为E. (1)求线段CD的长; (2)求cos∠ABE的值. 图5-G-10 7 1.B [解析] ∵Rt△ABC中,∠C=90°,AB=5,AC=2,∴cosA==.故选B. 2.C [解析] 在Rt△ABC中,∠BAC=90°, ∴∠B+∠C=90°,sinB=.∵AD⊥BC, ∴∠DAC+∠C=90°,sinB=,∴∠B=∠DAC,∴sinB=sin∠DAC=.综上,只有C不正确.故选C. 3.B 4.B [解析] ∵cosA=,∴∠A=60°, ∴sinA=. 5.B [解析] ∵cos45°=sin45°=,∴cos245°+sin245°=()2+()2=+=1. 6.B 7.D 8.D [解析] ∵cosB=,∴∠B=45°. 当△ABC为钝角三角形时,过点A作AD⊥BC,交BC的延长线于点D,如图①. ∵AB=12 ,∠B=45°,∴AD=BD=12. ∵AC=13,∴由勾股定理得CD=5, ∴BC=BD-CD=12-5=7; 当△ABC为锐角三角形时,过点A作AD⊥BC于点D,如图②,同理可得BC=BD+CD=12+5=17.故选D. 9. 10. [解析] ∵在△ABC中,∠C=90°,AB=5,BC=3,∴AC==4, ∴cosA==. 11. [解析] 过点A作AD⊥OB,垂足为D, 在Rt△AOD中,AD=1,OD=2, 则tan∠AOB==. 7 12.75 13.60 [解析] AD==10 cm, 所以菱形ABCD的边长是10 cm, 则菱形ABCD的面积是10×6=60(cm2). 14.> [解析] 由正方形网格图可知,tanα=,tanβ=,则tanα+tanβ=+=. ∵AC=BC,∠ACB=90°, ∴α+β=45°, ∴tan(α+β)=1, ∴tan(α+β)>tanα+tanβ. 15.8 [解析] 设DE=x,则CD=x,AC=9-x. ∵sinB=,DE⊥AB,∴BD=x, 由勾股定理,得BE=,则tanB=, ∴=,即=,解得x=3, ∴BC=x+x=8. 故答案为8. 16.解:原式=×+×-()2×1=+-=. 17.解:∵在Rt△ABC中,∠C=90°,∠A=60°, ∴∠B=30°,tanA=, ∴a=btanA=b,c=2b. 又∵a+b=2,∴b+b=2, ∴b=-1,∴c=2b=2 -2. 18.解:∵在Rt△ABD中,tan∠BAD==, ∴BD=AD·=12×=9, ∴CD=BC-BD=14-9=5, ∴AC===13, ∴sinC==. 19.解:tan75°=tan(30°+45°)==2+. 7 20.解:(1)在△ABC中,∵∠ACB=90°, ∴sinA==,而BC=8,∴AB=10. ∵D是AB的中点,∴CD=AB=5. (2)在Rt△ABC中,∵AB=10,BC=8, ∴AC==6. ∵D是AB的中点,∴BD=5,S△BDC=S△ADC, ∴S△BDC=S△ABC, 即CD·BE=·AC·BC, ∴BE==. 在Rt△BDE中,cos∠DBE===, 即cos∠ABE的值为. 7查看更多