2020年上海市杨浦区中考数学一模试卷
2020年上海市杨浦区中考数学一模试卷
一、选择题:(本大题共6题,每题4分,满分24分)
1. 将抛物线y=x2向左平移1个单位,所得抛物线解析式是( )
A.y=(x−1)2 B.y=(x+1)2 C.y=x2+1 D.y=x2−1
2. 在Rt△ABC中,∠C=90∘,如果AC=2,cosA=34,那么AB的长是( )
A.52 B.83 C.103 D.237
3. 已知a→、b→和c→都是非零向量,下列结论中不能判定a→ // b→的是( )
A.a→∥c→,b→∥c→ B.a→=12c→,b→=2c→
C.a→=2b→ D.|a→|=|b→|
4. 如图,在6×6的正方形网格中,联结小正方形中两个顶点A、B,如果线段AB与网格线的其中两个交点为M、N,那么AM:MN:NB的值是( )
A.3:5:4 B.3:6:5 C.1:3:2 D.1:4:2
5. 广场上喷水池中的喷头微露水面,喷出的水线呈一条抛物线,水线上水珠的高度y(米)关于水珠和喷头的水平距离x(米)的函数解析式是y=−32x2+6x(0≤x≤4),那么水珠的高度达到最大时,水珠与喷头的水平距离是( )
A.1米 B.2米 C.5米 D.6米
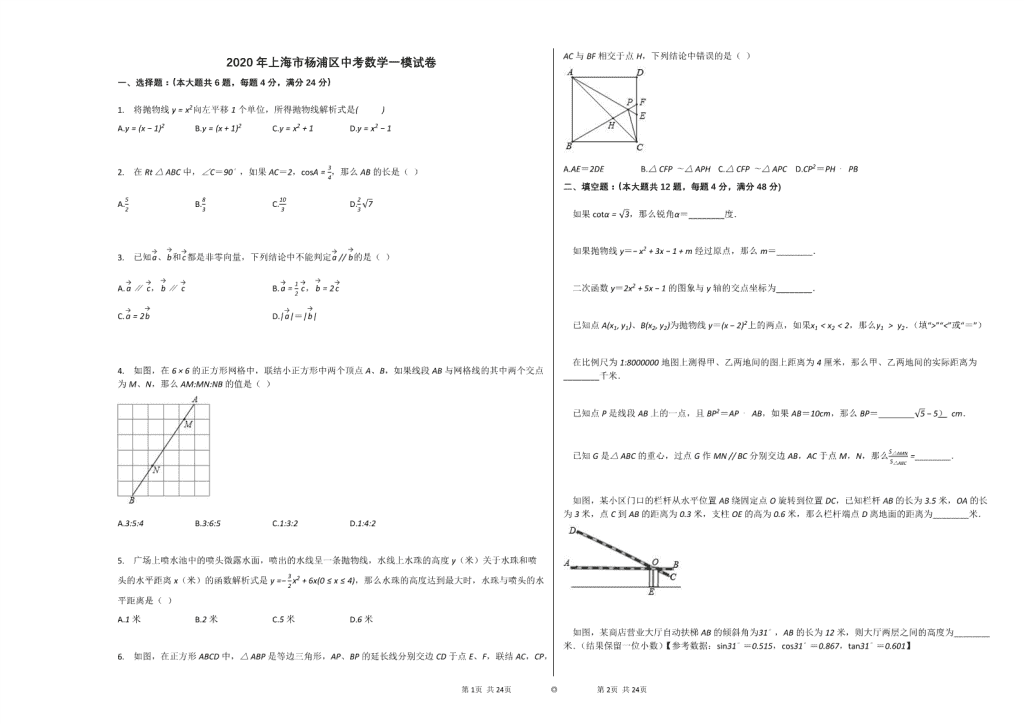
6. 如图,在正方形ABCD中,△ABP是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC,CP,AC与BF相交于点H,下列结论中错误的是( )
A.AE=2DE B.△CFP∼△APH C.△CFP∼△APC D.CP2=PH⋅PB
二、填空题:(本大题共12题,每题4分,满分48分)
如果cotα=3,那么锐角α=________度.
如果抛物线y=−x2+3x−1+m经过原点,那么m=________.
二次函数y=2x2+5x−1的图象与y轴的交点坐标为________.
已知点A(x1, y1)、B(x2, y2)为抛物线y=(x−2)2上的两点,如果x1
y2.(填“>”“<”或“=”)
在比例尺为1:8000000地图上测得甲、乙两地间的图上距离为4厘米,那么甲、乙两地间的实际距离为________千米.
已知点P是线段AB上的一点,且BP2=AP⋅AB,如果AB=10cm,那么BP=________5−5) cm.
已知G是△ABC的重心,过点G作MN // BC分别交边AB,AC于点M,N,那么S△AMNS△ABC=________.
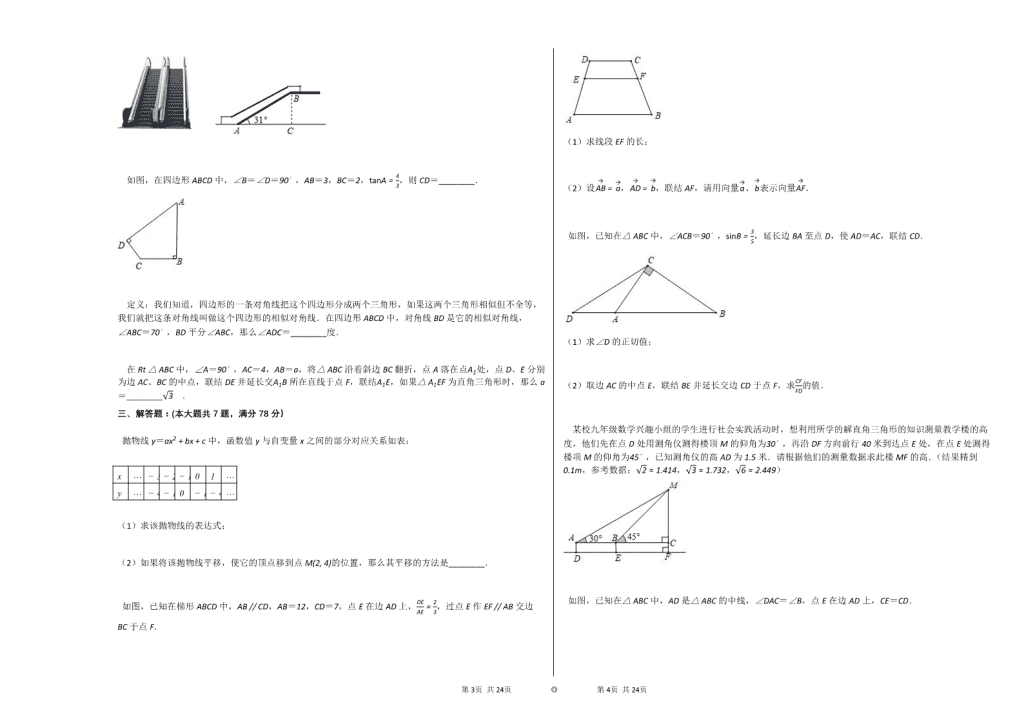
如图,某小区门口的栏杆从水平位置AB绕固定点O旋转到位置DC,已知栏杆AB的长为3.5米,OA的长为3米,点C到AB的距离为0.3米,支柱OE的高为0.6米,那么栏杆端点D离地面的距离为________米.
如图,某商店营业大厅自动扶梯AB的倾斜角为31∘,AB的长为12
第21页 共24页 ◎ 第22页 共24页
米,则大厅两层之间的高度为________米.(结果保留一位小数)【参考数据:sin31∘=0.515,cos31∘=0.867,tan31∘=0.601】
如图,在四边形ABCD中,∠B=∠D=90∘,AB=3,BC=2,tanA=43,则CD=________.
定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线.在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70∘,BD平分∠ABC,那么∠ADC=________度.
在Rt△ABC中,∠A=90∘,AC=4,AB=a,将△ABC沿着斜边BC翻折,点A落在点A1处,点D、E分别为边AC、BC的中点,联结DE并延长交A1B所在直线于点F,联结A1E,如果△A1EF为直角三角形时,那么a=________3 .
三、解答题:(本大题共7题,满分78分)
抛物线y=ax2+bx+c中,函数值y与自变量x之间的部分对应关系如表:
x
…
−3
−2
−1
0
1
…
y
…
−4
−1
0
−1
−4
…
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2, 4)的位置,那么其平移的方法是________.
如图,已知在梯形ABCD中,AB // CD,AB=12,CD=7,点E在边AD上,DEAE=23,过点E作EF // AB交边BC于点F.
(1)求线段EF的长;
(2)设AB→=a→,AD→=b→,联结AF,请用向量a→、b→表示向量AF→.
如图,已知在△ABC中,∠ACB=90∘,sinB=35,延长边BA至点D,使AD=AC,联结CD.
(1)求∠D的正切值;
(2)取边AC的中点E,联结BE并延长交边CD于点F,求CFFD的值.
某校九年级数学兴趣小组的学生进行社会实践活动时,想利用所学的解直角三角形的知识测量教学楼的高度,他们先在点D处用测角仪测得楼顶M的仰角为30∘,再沿DF方向前行40米到达点E处,在点E处测得楼项M的仰角为45∘,已知测角仪的高AD为1.5米.请根据他们的测量数据求此楼MF的高.(结果精到0.1m,参考数据:2≈1.414,3≈1.732,6≈2.449)
第21页 共24页 ◎ 第22页 共24页
如图,已知在△ABC中,AD是△ABC的中线,∠DAC=∠B,点E在边AD上,CE=CD.
(1)求证:ACAB=BDAD;
(2)求证:AC2=2AE⋅AD.
已知在平面直角坐标系xOy中,抛物线y=mx2−2mx+4(m≠0)与x轴交于点A,B(点A在点B的左侧),且AB=6.
(1)求这条抛物线的对称轴及表达式;
(2)在y轴上取点E(0, 2),点F为第一象限内抛物线上一点,联结BF,EF,如果S四边形OEFB=10,求点F的坐标;
(3)在第(2)小题的条件下,点F在抛物线对称轴右侧,点P在x轴上且在点B左侧,如果直线PF与y轴的夹角等于∠EBF,求点P的坐标.
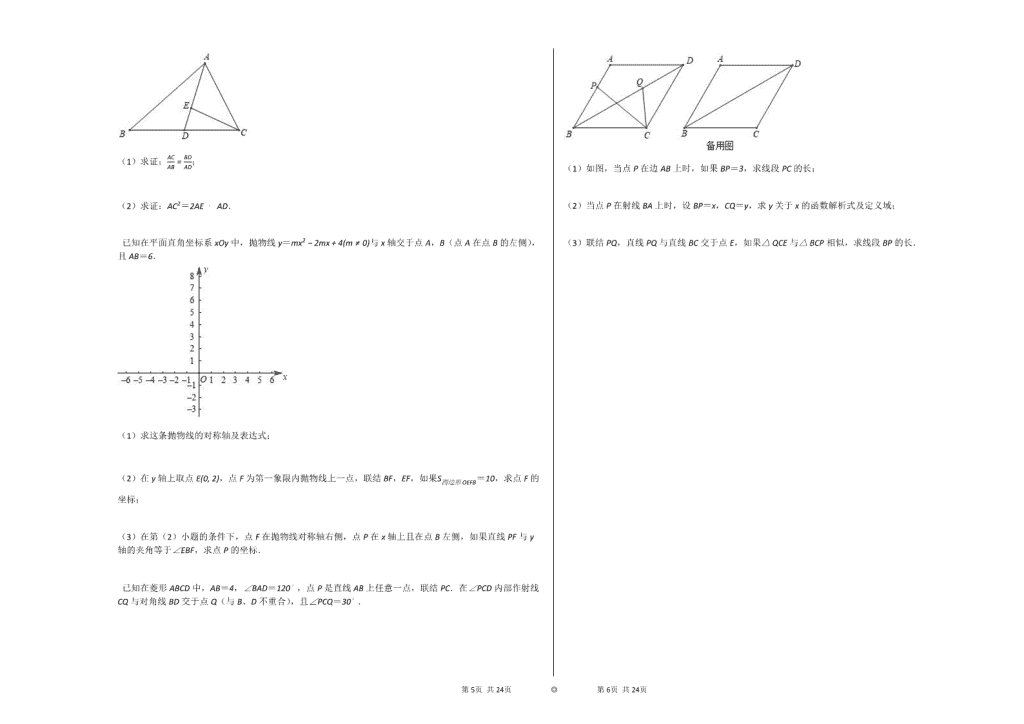
已知在菱形ABCD中,AB=4,∠BAD=120∘,点P是直线AB上任意一点,联结PC.在∠PCD内部作射线CQ与对角线BD交于点Q(与B、D不重合),且∠PCQ=30∘.
(1)如图,当点P在边AB上时,如果BP=3,求线段PC的长;
(2)当点P在射线BA上时,设BP=x,CQ=y,求y关于x的函数解析式及定义域;
(3)联结PQ,直线PQ与直线BC交于点E,如果△QCE与△BCP相似,求线段BP的长.
第21页 共24页 ◎ 第22页 共24页
参考答案与试题解析
2020年上海市杨浦区中考数学一模试卷
一、选择题:(本大题共6题,每题4分,满分24分)
1.
【答案】
B
【考点】
二次函数图象与几何变换
【解析】
根据“左加右减、上加下减”的原则进行解答即可.
【解答】
解:将抛物线y=x2向左平移1个单位,所得抛物线解析式是y=(x+1)2,
故选B.
2.
【答案】
B
【考点】
锐角三角函数的定义
【解析】
根据cosA=ACAB=34,求出AB即可.
【解答】
在Rt△ABC中,∵ ∠C=90∘,AC=2,
又∵ cosA=ACAB=34,
∴ AB=83,
3.
【答案】
D
【考点】
*平面向量
【解析】
根据平行向量的定义判断即可.
【解答】
A、由a→ // c→,b→ // c→,可以推出a→ // b→.本选项不符合题意.
B、由a→=12c→,b→=2c→,可以推出a→ // b→.本选项不符合题意.
C、由a→=2b→,可以推出a→ // b→.本选项不符合题意.
D、由|a→|=|b→|,不可以推出a→ // b→.本选项符合题意.
4.
【答案】
C
【考点】
相似三角形的性质与判定
【解析】
根据平行线分线段成比例定理得出即可.
【解答】
∵ AMMN=13,MNNB=32,
∴ AM:MN:NB=1:3:2,
5.
【答案】
B
【考点】
二次函数的应用
【解析】
根据二次函数的顶点式即可求解.
【解答】
方法一:
根据题意,得
y=−32x2+6x(0≤x≤4),
=−32(x−2)2+6
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
方法二:
因为对称轴x=62×32=2,
所以水珠的高度达到最大时,水珠与喷头的水平距离是2米.
6.
【答案】
C
【考点】
等边三角形的性质
相似三角形的性质与判定
正方形的性质
【解析】
①正确.利用直角三角形30度角的性质即可解决问题.
②正确,根据两角相等两个三角形相似即可判断.
③错误.通过计算证明∠CPA≠∠CPF,即可判断.
④正确.利用相似三角形的性质即可证明.
【解答】
∵ 四边形ABCD是正方形,
∴
第21页 共24页 ◎ 第22页 共24页
∠D=∠DAB=90∘,
∵ △APB是等边三角形,
∴ ∠PAB=∠PBA=∠APB=60∘,
∴ ∠DAE=30∘,
∴ AE=2DE,故①正确,
∵ AB // CD,
∴ ∠PFE=∠ABP=∠APH=60∘,
∵ ∠AHP=∠PBA+∠BAH=60∘+45∘=105∘,
又∵ BC=BP,∠PBC=30∘,
∴ ∠BPC=∠BCP=75∘,
∴ ∠CPF=105∘,
∴ ∠PHA=∠CPF,
∴ △CFP∽△APH,故②正确,
∵ ∠CPA=60∘+75∘=135∘≠∠CPF,
∴ △PFC与△PCA不相似,故③错误,
∵ ∠PCH=∠PCB−∠BCH=75∘−45∘=30∘,
∴ ∠PCH=∠PBC,
∵ ∠CPH=∠BPC,
∴ △PCH∽△PBC,
∴ PCPB=PHPC,
∴ CP2=PH⋅PB,故④正确,
二、填空题:(本大题共12题,每题4分,满分48分)
【答案】
30
【考点】
特殊角的三角函数值
【解析】
直接利用特殊角的三角函数值进而得出答案.
【解答】
∵ cotα=3,
∴ 锐角α=30∘.
【答案】
1
【考点】
二次函数图象上点的坐标特征
【解析】
把原点坐标代入y=−x2+3x−1+m中得到关于m的一次方程,然后解一次方程即可.
【解答】
∵ 抛物线y=−x2+3x−1+m经过点(0, 0),
∴ −1+m=0,
∴ m=1.
【答案】
(0, −1)
【考点】
二次函数图象上点的坐标特征
【解析】
根据y轴上点的坐标特征计算自变量为0时的函数值即可得到交点坐标.
【解答】
当x=0时,y=−1,
所以二次函数y=2x2+5x−1的图象与y轴的交点坐标为(0, −1).
【答案】
>
【考点】
二次函数图象上点的坐标特征
【解析】
根据二次函数的性质得到抛物线y=(x−2)2的开口向上,对称轴为直线x=2,则在对称轴左侧,y随x的增大而减小,所以x1y2.
【解答】
∵ y=(x−2)2,
∴ a=1>0,
∴ 抛物线开口向上,
∵ 抛物线y=(x−2)2对称轴为直线x=2,
∵ x1y2.
【答案】
320
【考点】
比例线段
【解析】
根据比例尺=代入数据计算即可.
【解答】
设甲、乙两地的实际距离为xcm,
∵ 比例尺=,
∴ 1:8000000=4:x,
∴ x=32000000,
∴ 甲、乙两地的实际距离为是320km,
【答案】
(5
【考点】
黄金分割
【解析】
根据点P是线段AB上的一点,且BP2=AP⋅AB,列方程即可求解.
【解答】
∵ 点P是线段AB上的一点
∴ AP=AB−BP=10−BP,
∵ BP2=AP⋅AB,AB=10cm,
BP2=(10−BP)×10,
解得BP=55−5.
第21页 共24页 ◎ 第22页 共24页
【答案】
49
【考点】
相似三角形的性质与判定
三角形的重心
【解析】
根据三角形重心和相似三角形的判定和性质解答即可.
【解答】
解:如图,连接AG并延长交BC于点E,
,
∵ 点G是△ABC的重心,
∴ AGGE=21,
∵ MN // BC,
∴ △AMN∼△ABC,
∴ S△AMNS△ABC=(AGAE)2=49,
故答案为:49.
【答案】
2.4
【考点】
相似三角形的应用
旋转的性质
【解析】
过D作DG⊥AB于G,过C作CH⊥AB于H,则DG // CH,根据相似三角形的性质即可得到结论.
【解答】
过D作DG⊥AB于G,过C作CH⊥AB于H,
则DG // CH,
∴ △ODG∽△OCH,
∴ DGCH=ODOC,
∵ 栏杆从水平位置AB绕固定点O旋转到位置DC,
∴ CD=AB=3.5m,OD=OA=3m,CH=0.3m,
∴ OC=0.5m,
∴ DG0.3=30.5,
∴ DG=1.8m,
∵ OE=0.6m,
∴ 栏杆D端离地面的距离为1.8+0.6=2.4m.
【答案】
6.2
【考点】
解直角三角形的应用-坡度坡角问题
【解析】
根据题意和锐角三角函数可以求得BC的长,从而可以解答本题.
【解答】
在Rt△ABC中,
∵ ∠ACB=90∘,
∴ BC=AB⋅sin∠BAC=12×0.515≈6.2(米),
答:大厅两层之间的距离BC的长约为6.2米.
故答案为:6.2.
【答案】
65
【考点】
解直角三角形
【解析】
延长AD和BC交于点E,在直角△ABE中利用三角函数求得BE的长,则EC的长即可求得,然后在直角△CDE中利用三角函数的定义求解.
【解答】
延长AD和BC交于点E.
∵ 在直角△ABE中,tanA=BEAB=43,AB=3,
∴ BE=4,
∴ EC=BE−BC=4−2=2,
∵ △ABE和△CDE中,∠B=∠EDC=90∘,∠E=∠E,
∴ ∠DCE=∠A,
∴ 直角△CDE中,tan∠DCE=tanA=DEDC=43,
∴ 设DE=4x,则DC=3x,
在直角△CDE中,EC2=DE2+DC2,
∴ 4=16x2+9x2,
解得:x=25,
则CD=65.
【答案】
145
【考点】
相似图形
【解析】
依据四边形的相似对角线的定义,即可得到∠ABD=∠DBC,∠A=∠BDC,∠ADB=∠C,再根据四边形内角和为360∘,即可得到∠ADC的度数.
第21页 共24页 ◎ 第22页 共24页
【解答】
如图所示,∵ ∠ABC=70∘,BD平分∠ABC,
∴ ∠ABD=∠DBC,
又∵ 对角线BD是它的相似对角线,
∴ △ABD∽△DBC,
∴ ∠A=∠BDC,∠ADB=∠C,
∴ ∠A+∠C=∠ADC,
又∵ ∠A+∠C+∠ADC=360∘−70∘=290∘,
∴ ∠ADC=145∘,
【答案】
4或4
【考点】
勾股定理
翻折变换(折叠问题)
三角形中位线定理
【解析】
当△A1EF为直角三角形时,存在两种情况:
①当∠A1EF=90∘时,如图1,根据对称的性质和平行线可得:A1C=A1E=4,根据直角三角形斜边中线的性质得:BC=2A1B=8,最后利用勾股定理可得AB的长;
②当∠A1FE=90∘时,如图2,证明△ABC是等腰直角三角形,可得AB=AC=4.
【解答】
当△A1EF为直角三角形时,存在两种情况:
①当∠A1EF=90∘时,如图1,
∵ △A1BC与△ABC关于BC所在直线对称,
∴ A1C=AC=4,∠ACB=∠A1CB,
∵ 点D,E分别为AC,BC的中点,
∴ D、E是△ABC的中位线,
∴ DE // AB,
∴ ∠CDE=∠MAN=90∘,
∴ ∠CDE=∠A1EF,
∴ AC // A1E,
∴ ∠ACB=∠A1EC,
∴ ∠A1CB=∠A1EC,
∴ A1C=A1E=4,
Rt△A1CB中,
∵ E是斜边BC的中点,
∴ BC=2A1E=8,
由勾股定理得:AB2=BC2−AC2,
∴ AB=82−42=43;
②当∠A1FE=90∘时,如图2,
∵ ∠ADF=∠A=∠DFB=90∘,
∴ ∠ABF=90∘,
∵ △A1BC与△ABC关于BC所在直线对称,
∴ ∠ABC=∠CBA1=45∘,
∴ △ABC是等腰直角三角形,
∴ AB=AC=4;
综上所述,AB的长为43或4;
三、解答题:(本大题共7题,满分78分)
【答案】
∵ 抛物线y=ax2+bx+c过点(−1, 0),(0, −1),(1, −4),
∴ a−b+c=0a+b+c=4c=−1 ,
解得a=−1b=−2c=−1 ,
∴ 该抛物线的表达式为y=−x2−2x−1;
向右平移3个单位,向上平移4个单位
【考点】
待定系数法求二次函数解析式
二次函数图象上点的坐标特征
二次函数的性质
二次函数图象与几何变换
【解析】
(1)将(−1, 0),(0, −1),(1, −4)代入抛物线解析式y=ax2+bx+c中即可得解;
(2)根据“上加下减,左加右减”的原则进行解答即可.
【解答】
∵ 抛物线y=ax2+bx+c过点(−1, 0),(0, −1),(1, −4),
∴ a−b+c=0a+b+c=4c=−1 ,
解得a=−1b=−2c=−1 ,
∴ 该抛物线的表达式为y=−x2−2x−1;
∵ 新顶点M(2, 4),
∴ y=−(x−2)2+4,
∵ y=−x2−2x−1=−(x+1)2,
∴ 抛物线的表达式为y=−x2−2x−1向右平移3个单位,向上平移4个单位可得到y=−(x−2)2+4,
故答案为:向右平移3个单位,向上平移4个单位.
【答案】
第21页 共24页 ◎ 第22页 共24页
过D作DM // BC交EF于N,交AB于M,则BM=FN=CD=7,
∴ AM=AB−BM=12−7=5,
∵ DEAE=23,
∴ DEDA=ENAM=25
∴ EN=2,
∴ EF=EN+FN=2+7=9;
∵ EF=9,AB=12,
∴ EFAB=34,
∵ AB→=a→,
∴ EF→=34AB→=34a→,
∵ AEAD=35,AD→=b→,
∴ AE→=35b→,
∴ AF→=AE→+EF→=35b→+34a→.
【考点】
*平面向量
梯形
相似三角形的性质与判定
【解析】
(1)过D作DM // BC交EF于N,交AB于M,则BM=FN=CD=7,根据平行线分线段成比例定理即可得到结论;
(2)根据平行线分线段成比例定理即可得到结论.
【解答】
过D作DM // BC交EF于N,交AB于M,则BM=FN=CD=7,
∴ AM=AB−BM=12−7=5,
∵ DEAE=23,
∴ DEDA=ENAM=25
∴ EN=2,
∴ EF=EN+FN=2+7=9;
∵ EF=9,AB=12,
∴ EFAB=34,
∵ AB→=a→,
∴ EF→=34AB→=34a→,
∵ AEAD=35,AD→=b→,
∴ AE→=35b→,
∴ AF→=AE→+EF→=35b→+34a→.
【答案】
过点C作CG⊥AB,垂足为G,
∵ ∠ACB=90∘,
∴ ∠ACG=∠B,
在△ABC中,sinB=35,设AC=3x,则AB=5x,BC=4x,
∴ sin∠ACG=AGAC=35=sinB,
∴ AG=95x,CG=125x,
∴ DG=DA+AG=3x+95x=245x,
在Rt△DCG中,tan∠D=CGDG=12;
过点C作CF // DB,交BF的延长线于点H,则有△CHF∽△DBF,
又有E是AC的中点,可证△CHE≅△ABE,
∴ HC=AB=5x,
由△CHF∽△DBF得:CFDF=CHDB=5x3x+5x=58.
【考点】
解直角三角形
等腰三角形的性质
【解析】
第21页 共24页 ◎ 第22页 共24页
(1)作高构造直角三角形,设AC=3x,表示出CG、AG、DG,再利用直角三角形的边角关系,求出∠D正切值;
(2)过点C作CF // DB,交BF的延长线于点H,相似三角形、全等三角形,进而得出HC=AB=5x,将:CFDF转化为求HCDB即可.
【解答】
过点C作CG⊥AB,垂足为G,
∵ ∠ACB=90∘,
∴ ∠ACG=∠B,
在△ABC中,sinB=35,设AC=3x,则AB=5x,BC=4x,
∴ sin∠ACG=AGAC=35=sinB,
∴ AG=95x,CG=125x,
∴ DG=DA+AG=3x+95x=245x,
在Rt△DCG中,tan∠D=CGDG=12;
过点C作CF // DB,交BF的延长线于点H,则有△CHF∽△DBF,
又有E是AC的中点,可证△CHE≅△ABE,
∴ HC=AB=5x,
由△CHF∽△DBF得:CFDF=CHDB=5x3x+5x=58.
【答案】
楼MF的高56.1米
【考点】
解直角三角形的应用-仰角俯角问题
【解析】
首先分析图形,根据题意构造直角三角形.本题涉及多个直角三角形,应利用其公共边构造三角关系,进而可求出答案.
【解答】
设MC=x,
∵ ∠MAC=30∘,
∴ 在Rt△MAC中,AC=MCtan∠MAC=x33=3x.
∵ ∠MBC=45∘,
∴ 在Rt△MCB中,MC=BC=x,
又∵ AB=DE=40,
∴ AC−BC=AB=40,即3x−x=40,
解得:x=20+203≈54.6,
∴ MF=MC+CF=54.6+1.5=56.1(米),
【答案】
证明:∵ CD=CE,
∴ ∠CED=∠EDC,
∵ ∠AEC+∠CED=180∘,∠ADB+∠EDC=180∘,
∴ ∠AEC=∠ADB,
∵ ∠DAC=∠B
∴ △ACE∽△BAD;
∵ ∠DAC=∠B,∠ACD=∠BCA,
∴ △ACD∽△BCA,
∴ ACCD=CBCA,
∴ AC2=CD⋅CB,
∵ △ACE∽△BAD,
∴ AEBD=CEAD,
∴ AE⋅AD=BD⋅CE,
∴ 2AE⋅AD=2BD⋅CE=BC⋅CD,
∴ AC2=2AE⋅AD.
【考点】
相似三角形的性质与判定
【解析】
(1)先利用等腰三角形的性质,由CD=CE得到∠CED=∠EDC,则可根据等角的补角相等得到∠AEC=∠ADB,加上∠DAC=∠B,于是可根据有两组角对应相等的两个三角形相似判断△ACE∽△BAD.
(2)由∠DAC=∠B及公共角相等证明△ACD∽△BCA,利用相似比即可得到结论.
【解答】
证明:∵ CD=CE,
∴ ∠CED=∠EDC,
∵ ∠AEC+∠CED=180∘,∠ADB+∠EDC=180∘,
∴ ∠AEC=∠ADB,
∵ ∠DAC=∠B
∴ △ACE∽△BAD;
∵ ∠DAC=∠B,∠ACD=∠BCA,
∴ △ACD∽△BCA,
∴ ACCD=CBCA,
∴ AC2=CD⋅CB,
∵ △ACE∽△BAD,
∴ AEBD=CEAD,
∴ AE⋅AD=BD⋅CE,
∴ 2AE⋅AD=2BD⋅CE=BC⋅CD,
∴ AC2=2AE⋅AD.
【答案】
由y=mx2−2mx+4=m(x−1)2+4−m得到:抛物线对称轴为直线x=1.
∵ AB=6,
∴ A(−2, 0),B(4, 0).
将点A
第21页 共24页 ◎ 第22页 共24页
的坐标代入函数解析式得到:4m+4m+4=0,解得m=−12.
故该抛物线解析式是:y=−12x2+x+4;
如图1,联结OF,
设F(t, −12t2+t+4),则
S四边形OEFB=S△OEF+S△OFB=12×2t+12×4(−12t2+t+4)=10.
∴ t1=1,t2=2.
∴ 点F的坐标是(1, 92)或(2, 4);
由题意得,F(2, 4),
如图2,设PF与y轴的交点为G.,
∵ tan∠EBO=OEOB=24=12,tan∠HFB=BHFH=12,
∴ tan∠EBO=tan∠HFB.
∴ ∠EBO=∠HFB.
又∵ ∠PFH=∠EGF=∠FBE,
∴ ∠PFB=∠PBF.
∴ PF=PB.
设P(a, 0).
则PF=PB,
∴ (a−4)2=(a−2)2+42,解得a=−1.
∴ P(−1, 0)
【考点】
二次函数综合题
【解析】
(1)根据抛物线解析式求得对称轴方程为x=1,结合AB=6求得点A、B的坐标;然后利用待定系数法确定函数解析式;
(2)如图1,联结OF,设F(t, −12t2+t+4),根据图形得到S四边形OEFB=S△OEF+S△OFB,由三角形的面积公式列出方程,利用方程求得点F的横坐标,结合二次函数图象上点的坐标特征求得点F的纵坐标;
(3)如图2,设PF与y轴的交点为G.由tan∠EBO=tan∠HFB=12得到:∠EBO=∠HFB.易推知∠PFB=∠PBF.故PF=PB.设P(a, 0).由两点间的距离公式求得相关线段的长度并列出方程,通过解方程求得点P的横坐标.
【解答】
由y=mx2−2mx+4=m(x−1)2+4−m得到:抛物线对称轴为直线x=1.
∵ AB=6,
∴ A(−2, 0),B(4, 0).
将点A的坐标代入函数解析式得到:4m+4m+4=0,解得m=−12.
故该抛物线解析式是:y=−12x2+x+4;
如图1,联结OF,
设F(t, −12t2+t+4),则
S四边形OEFB=S△OEF+S△OFB=12×2t+12×4(−12t2+t+4)=10.
∴ t1=1,t2=2.
∴ 点F的坐标是(1, 92)或(2, 4);
由题意得,F(2, 4),
如图2,设PF与y轴的交点为G.,
∵ tan∠EBO=OEOB=24=12
第21页 共24页 ◎ 第22页 共24页
,tan∠HFB=BHFH=12,
∴ tan∠EBO=tan∠HFB.
∴ ∠EBO=∠HFB.
又∵ ∠PFH=∠EGF=∠FBE,
∴ ∠PFB=∠PBF.
∴ PF=PB.
设P(a, 0).
则PF=PB,
∴ (a−4)2=(a−2)2+42,解得a=−1.
∴ P(−1, 0)
【答案】
如图1中,作PH⊥BC于H.
∵ 四边形ABCD是菱形,
∴ AB=BC=4,AD // BC,
∴ ∠A+∠ABC=180∘,
∵ ∠A=120∘,
∴ ∠PBH=60∘,
∵ PB=3,∠PHB=90∘,
∴ BH=PB⋅cos60∘=32,PH=PB⋅sin60∘=332,
∴ CH=BC−BH=4−32=52,
∴ PC=PH2+CH2=(332)2+(52)2=13.
如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵ 四边形ABCD是菱形,
∴ ∠ABD=∠CBD=30∘,
∵ ∠PCQ=30∘,
∴ ∠PBO=∠QCO,
∵ ∠POB=∠QOC,
∴ △POB∽△QOC,
∴ POQO=BOCD,
∴ OPBO=QOCD,
∵ ∠POQ=∠BOC,
∴ △POQ∽△BOC,
∴ ∠OPQ=∠OBC=30∘=∠PCQ,
∴ PQ=CQ=y,
∴ PC=3y,
在Rt△PHB中,BH=12x,PH=32x,
∵ PC2=PH2+CH2,
∴ 3y2=(32x)2+(4−12x)2,
∴ y=3x2−12x+483(0≤x<8).
①如图2中,若直线QP交直线BC于B点左侧于E.
此时∠CQE=120∘,
∵ ∠PBC=60∘,
∴ △PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.
②如图3中,若直线QP交直线BC于C点右侧于E.
则∠CQE=∠B=QBC+∠QCP=60∘=∠CBP,
∵ ∠PCB>∠E,
∴ 只可能∠BCP=∠QCE=75∘,
作CF⊥AB于F,则BF=2,CF=23,∠PCF=45∘,
∴ PF=CF=23,
此时PB2+23,
综上所述,满足条件的PB
第21页 共24页 ◎ 第22页 共24页
的值为2+23.
【考点】
相似三角形综合题
【解析】
(1)如图1中,作PH⊥BC于H.解直角三角形求出BH,PH,在Rt△PCH中,理由勾股定理即可解决问题.
(2)如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.证明△POQ∽△BOC,推出∠OPQ=∠OBC=30∘=∠PCQ,推出PQ=CQ=y,推出PC=3y,在Rt△PHB中,BH=12x,PH=32x,根据PC2=PH2+CH2,可得结论.
(3)分两种情形:①如图2中,若直线QP交直线BC于B点左侧于E.②如图3中,若直线QP交直线BC于C点右侧于E.分别求解即可.
【解答】
如图1中,作PH⊥BC于H.
∵ 四边形ABCD是菱形,
∴ AB=BC=4,AD // BC,
∴ ∠A+∠ABC=180∘,
∵ ∠A=120∘,
∴ ∠PBH=60∘,
∵ PB=3,∠PHB=90∘,
∴ BH=PB⋅cos60∘=32,PH=PB⋅sin60∘=332,
∴ CH=BC−BH=4−32=52,
∴ PC=PH2+CH2=(332)2+(52)2=13.
如图1中,作PH⊥BC于H,连接PQ,设PC交BD于O.
∵ 四边形ABCD是菱形,
∴ ∠ABD=∠CBD=30∘,
∵ ∠PCQ=30∘,
∴ ∠PBO=∠QCO,
∵ ∠POB=∠QOC,
∴ △POB∽△QOC,
∴ POQO=BOCD,
∴ OPBO=QOCD,
∵ ∠POQ=∠BOC,
∴ △POQ∽△BOC,
∴ ∠OPQ=∠OBC=30∘=∠PCQ,
∴ PQ=CQ=y,
∴ PC=3y,
在Rt△PHB中,BH=12x,PH=32x,
∵ PC2=PH2+CH2,
∴ 3y2=(32x)2+(4−12x)2,
∴ y=3x2−12x+483(0≤x<8).
①如图2中,若直线QP交直线BC于B点左侧于E.
此时∠CQE=120∘,
∵ ∠PBC=60∘,
∴ △PBC中,不存在角与∠CQE相等,
此时△QCE与△BCP不可能相似.
②如图3中,若直线QP交直线BC于C点右侧于E.
则∠CQE=∠B=QBC+∠QCP=60∘=∠CBP,
∵ ∠PCB>∠E,
∴ 只可能∠BCP=∠QCE=75∘,
作CF⊥AB于F,则BF=2,CF=23,∠PCF=45∘,
∴ PF=CF=23,
此时PB2+23,
综上所述,满足条件的PB的值为2+23.
第21页 共24页 ◎ 第22页 共24页