2018福建各地市九年级上期末数学质检卷及答案

2018福建各地市九年级上期末数学质检卷及答案

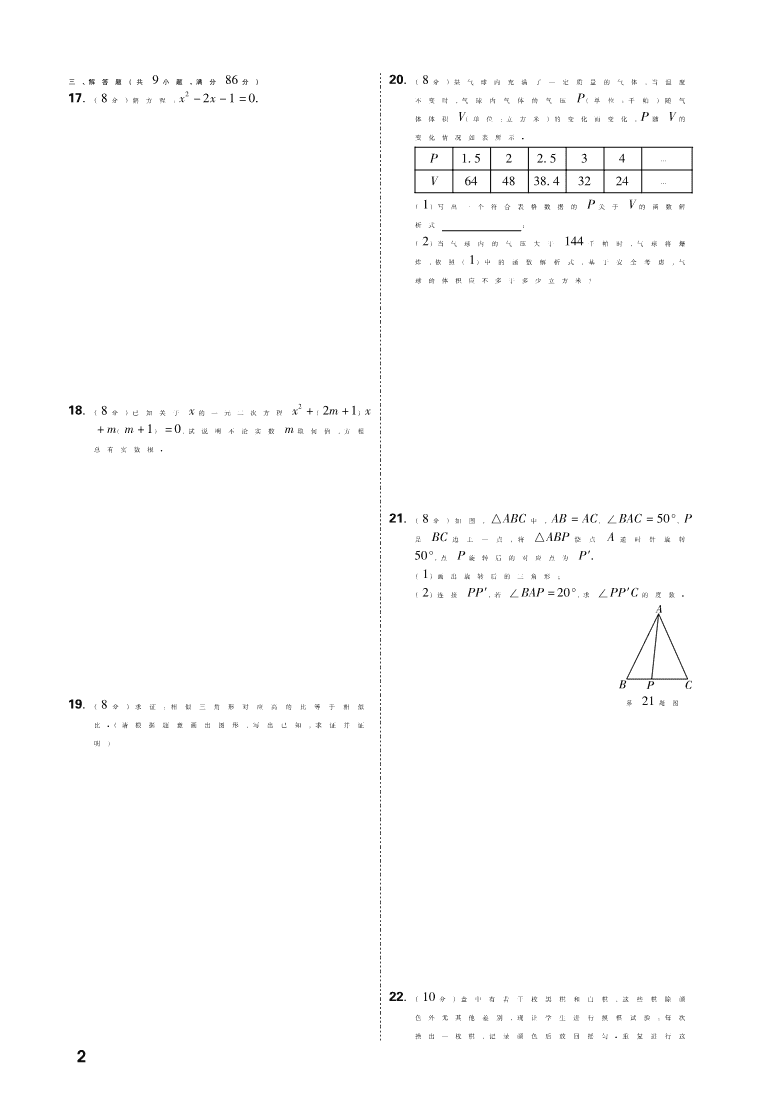
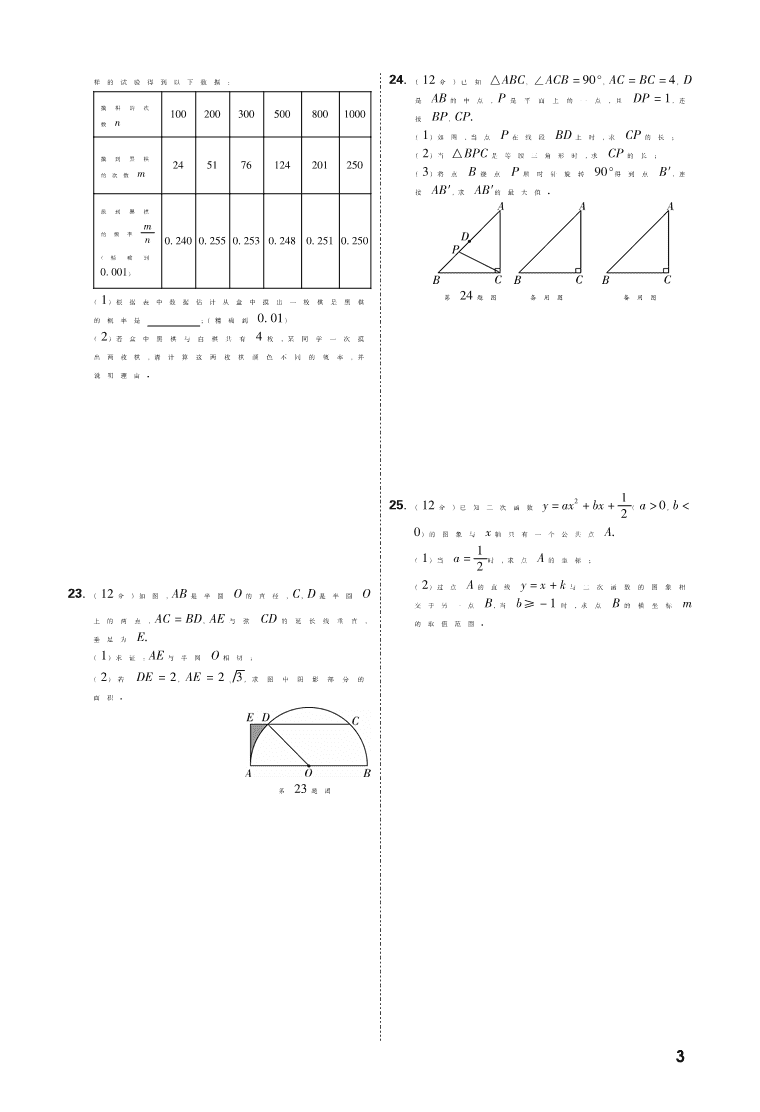
书书书 ２０１７－２０１８学年福建省福州市九年级（上） 期末数学试卷 （满分：１５０分　考试时间：１２０分钟） 　　　　　　　　　　　　　　　　　　一、选择题（共 １０小题，每小题 ４分，满分 ４０分） １．一元二次方程 ｘ２ －３ｘ＝０的解为 （　　） Ａ．ｘ１ ＝３，ｘ２ ＝－３ Ｂ．ｘ１ ＝－３，ｘ２ ＝０ Ｃ．ｘ１ ＝３，ｘ２ ＝０ Ｄ．ｘ１ ＝ｘ２ ＝３ ２．下列是中心对称图形但不是轴对称图形的是 （　　） ３．下列事件中，是随机事件的是 （　　） Ａ．任意画一个三角形，其内角和是 ３６０° Ｂ．任意抛一枚图钉，钉尖着地 Ｃ．通常加热到 １００℃时，水沸腾 Ｄ．太阳从东方升起 ４．二次函数 ｙ＝（ｘ－１）２ ＋２图象的顶点坐标是 （　　） Ａ．（－２，１） Ｂ．（２，１） Ｃ．（２，－１） Ｄ．（１，２） ５．下列图形中，正多边形内接于半径相等的圆，其中 正多边形周长最大的是 （　　） ６．某医药厂两年前生产 １ｔ某种药品的成本是 ５０００ 元，随着生产技术的进步，现在生产 １ｔ该种药品的 成本是 ３０００元．设该种药品生产成本的年平均下 降率为 ｘ，则下列所列方程正确的是 （　　） Ａ．５０００×２（１－ｘ）＝３０００ Ｂ．５０００×（１－ｘ）２ ＝３０００ Ｃ．５０００×（１－２ｘ）＝３０００ Ｄ．５０００×（１－ｘ２）＝３０００ ７．已知反比例函数 ｙ＝ｋ ｘ（ｋ＜０）的图象经过点 Ａ（－１， ｙ１），Ｂ（２，ｙ２），Ｃ（３，ｙ３），则 ｙ１，ｙ２，ｙ３的大小关系是 （　　） Ａ．ｙ２ ＜ｙ３ ＜ｙ１ Ｂ．ｙ３ ＜ｙ２ ＜ｙ１ Ｃ．ｙ１ ＜ｙ３ ＜ｙ２ Ｄ．ｙ１ ＜ｙ２ ＜ｙ３ ８．如图，在 ６×６的正方形网格中，有 ６个点 Ｍ，Ｎ，Ｏ， Ｐ，Ｑ，Ｒ（除 Ｒ外其余 ５个点均为格点），以 Ｏ为圆 心，ＯＱ为半径作圆，则在⊙Ｏ外的点是 （　　） Ａ．Ｍ Ｂ．Ｎ Ｃ．Ｐ Ｄ．Ｒ 第 ８题图 　　 第 ９题图 ９．如图，已知⊙Ｐ与坐标轴交于点 Ａ，Ｏ，Ｂ，点 Ｃ在 ⊙Ｐ上，且∠ＡＣＯ＝６０°，若点 Ｂ的坐标为（０，３），则 ) ＯＡ的长为 （　　） Ａ．２π Ｂ．３π 槡Ｃ． ３π 槡Ｄ．２ ３π １０．若二次函数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ的图象与 ｘ轴交于 Ａ 和 Ｂ两点，顶点为 Ｃ，且 ｂ２ －４ａｃ＝４，则∠ＡＣＢ的 度数为 （　　） Ａ．３０° Ｂ．４５° Ｃ．６０° Ｄ．９０° 二、填空题（共 ６小题，每小题 ４分，满分 ２４分） １１．已知反比例函数的图象过点（２，３），则该函数的 解析式为　　　　　　　． １２．有长为 ３，４，５，６的四根细木条，从中任取三根为 边组成三角形，则能构成直角三角形的概率为 　　　　． １３．抛物线 ｙ＝ｘ２ －４ｘ不经过第　　　　象限． １４．我国古代数学著作《九章算术》中记载了一个问 题：“今有邑方不知大小，各开中门，出北门三十 步有木，出西门七百五十步见木，问：邑方几何？” 其大意是：如图，一座正方形城池，Ａ为北门中点， 从点 Ａ往正北方向走 ３０步到 Ｂ处有一树木，Ｃ为 西门中点，从点 Ｃ往正西方向走 ７５０步到 Ｄ处正 好看 到 Ｂ处 的 树 木，则 正 方 形 城 池 的 边 长 为 　　　　步． 第 １４题图 １５．在平面直角坐标系中，点 Ｐ关于原点及点（０， －１）的 对 称 点 分 别 为 Ａ，Ｂ，则 ＡＢ 的 长 为 　　　　． 第 １６题图 １６．如图，在△ＡＢＣ中，ＡＢ∶ＡＣ＝７∶ ３，∠ＢＡＣ的平分线交 ＢＣ于点 Ｅ，过点 Ｂ作 ＡＥ的垂线段，垂足 为 Ｄ，则 ＡＥ∶ＥＤ＝　　　　                                                               ． １ 三、解答题（共 ９小题，满分 ８６分） １７．（８分）解方程：ｘ２ －２ｘ－１＝０． １８．（８分）已知关于 ｘ的一元二次方程 ｘ２ ＋（２ｍ＋１）ｘ ＋ｍ（ｍ＋１）＝０，试说明不论实数 ｍ取何值，方程 总有实数根． １９．（８分）求证：相似三角形对应高的比等于相似 比．（请根据题意画出图形，写出已知，求证并证 明） ２０．（８分）某气球内充满了一定质量的气体，当温度 不变时，气球内气体的气压 Ｐ（单位：千帕）随气 体体积 Ｖ（单位：立方米）的变化而变化，Ｐ随 Ｖ的 变化情况如表所示． Ｐ １．５ ２ ２．５ ３ ４ … Ｖ ６４ ４８ ３８．４ ３２ ２４ … （１）写出一个符合表格数据的 Ｐ关于 Ｖ的函数解 析式　　　　　　； （２）当气球内的气压大于 １４４千帕时，气球将爆 炸，依照（１）中的函数解析式，基于安全考虑，气 球的体积应不多于多少立方米？ ２１．（８分）如图，△ＡＢＣ中，ＡＢ＝ＡＣ，∠ＢＡＣ＝５０°，Ｐ 是 ＢＣ边上一点，将 △ＡＢＰ绕点 Ａ逆时针旋转 ５０°，点 Ｐ旋转后的对应点为 Ｐ′． （１）画出旋转后的三角形； （２）连接 ＰＰ′，若∠ＢＡＰ＝２０°，求∠ＰＰ′Ｃ的度数． 第 ２１题图 ２２．（１０分）盒中有若干枚黑棋和白棋，这些棋除颜 色外无其他差别，现让学生进行摸棋试验：每次 摸出一枚棋，记录颜色后放回摇匀．                                                                       重复进行这 ２ 样的试验得到以下数据： 摸 棋 的 次 数 ｎ １００ ２００ ３００ ５００ ８００ １０００ 摸 到 黑 棋 的次数 ｍ ２４ ５１ ７６ １２４ ２０１ ２５０ 摸 到 黑 棋 的 频 率 ｍ ｎ （精 确 到 ０．００１） ０．２４００．２５５０．２５３ ０．２４８ ０．２５１ ０．２５０ （１）根据表中数据估计从盒中摸出一枚棋是黑棋 的概率是　　　　；（精确到 ０．０１） （２）若盒中黑棋与白棋共有 ４枚，某同学一次摸 出两枚棋，请计算这两枚棋颜色不同的概率，并 说明理由． ２３．（１２分）如图，ＡＢ是半圆 Ｏ的直径，Ｃ，Ｄ是半圆 Ｏ 上的两点， ) ＡＣ＝ ) ＢＤ，ＡＥ与弦 ＣＤ的延长线垂直， 垂足为 Ｅ． （１）求证：ＡＥ与半圆 Ｏ相切； （２）若 ＤＥ＝２，ＡＥ 槡＝２ ３，求 图 中 阴 影 部 分 的 面积． 第 ２３题图 ２４．（１２分）已知△ＡＢＣ，∠ＡＣＢ＝９０°，ＡＣ＝ＢＣ＝４，Ｄ 是 ＡＢ的中点，Ｐ是平面上的一点，且 ＤＰ＝１，连 接 ＢＰ，ＣＰ． （１）如图，当点 Ｐ在线段 ＢＤ上时，求 ＣＰ的长； （２）当△ＢＰＣ是等腰三角形时，求 ＣＰ的长； （３）将点 Ｂ绕点 Ｐ顺时针旋转 ９０°得到点 Ｂ′，连 接 ＡＢ′，求 ＡＢ′的最大值． 第 ２４题图　　备用图　　　　备用图 ２５．（１２分）已知二次函数 ｙ＝ａｘ２ ＋ｂｘ＋１ ２（ａ＞０，ｂ＜ ０）的图象与 ｘ轴只有一个公共点 Ａ． （１）当 ａ＝１ ２时，求点 Ａ的坐标； （２）过点 Ａ的直线 ｙ＝ｘ＋ｋ与二次函数的图象相 交于另一点 Ｂ，当 ｂ≥ －１时，求点 Ｂ的横坐标 ｍ 的取值范围                                                                       ． ３ ２０１７－２０１８学年厦门市九年级（上）期末 数学试卷 （满分：１５０分　考试时间：１２０分钟） 　　　　　　　　 　　　　　　　　　　一、选择题（本大题有 １０小题，每小题 ４分，共 ４０分． 每小题都有四个选项，其中有且只有一个选项正确） １．下列算式中，计算结果是负数的是 （　　） Ａ．（－２）＋７ Ｂ．｜－１｜ Ｃ．３×（－２） Ｄ．（－１）２ ２．对于一元二次方程 ｘ２ －２ｘ＋１＝０，根的判别式 ｂ２ －４ａｃ中的 ｂ表示的数是 （　　） Ａ．－２ Ｂ．２ Ｃ．－１ Ｄ．１ ３．如图，四边形 ＡＢＣＤ的对角线 ＡＣ，ＢＤ交于点 Ｏ，Ｅ 是 ＢＣ边 上 一 点，连 接 ＡＥ，ＯＥ，则 下 列 角 中 是 △ＡＥＯ的外角的是 （　　） 第 ３题图 Ａ．∠ＡＥＢ Ｂ．∠ＡＯＤ Ｃ．∠ＯＥＣ Ｄ．∠ＥＯＣ ４．已知 ⊙Ｏ的半径是 ３，Ａ，Ｂ，Ｃ三点在 ⊙Ｏ 上， ∠ＡＣＢ＝６０°，则 ) ＡＢ的长是 （　　） Ａ．２π Ｂ．π Ｃ．３ ２π Ｄ．１ ２π ５．某区 ２５位学生参加魔方速拧比赛，比赛成绩如图 所示，则这 ２５个成绩的中位数是 （　　） 第 ５题图 Ａ．１１ Ｂ．１０．５ Ｃ．１０ Ｄ．６ ６．随着生产技术的进步，某厂生产一件产品的成本 从两年前的 １００元，下降到现在的 ６４元，求年平 均下降率，设年平均下降率为 ｘ，通过解方程得到 一个根为 １．８，则正确的解释是 （　　） Ａ．年平均下降率为 ８０％，符合题意 Ｂ．年平均下降率为 １８％，符合题意 Ｃ．年平均下降率为 １．８％，不符合题意 Ｄ．年平均下降率为 １８０％，不符合题意 ７．已知某二次函数，当 ｘ＜１时，ｙ随 ｘ的增大而减 小；当 ｘ＞１时，ｙ随 ｘ的增大而增大，则该二次函 数的解析式可以是 （　　） Ａ．ｙ＝２（ｘ＋１）２ Ｂ．ｙ＝２（ｘ－１）２ Ｃ．ｙ＝－２（ｘ＋１）２ Ｄ．ｙ＝－２（ｘ－１）２ ８．如图，已知 Ａ，Ｂ，Ｃ，Ｄ是圆上的点， ) ＡＤ＝ ) ＢＣ，ＡＣ， ＢＤ交于点 Ｅ，则下列结论正确的是 （　　） 第 ８题图 Ａ．ＡＢ＝ＡＤ Ｂ．ＢＥ＝ＣＤ Ｃ．ＡＣ＝ＢＤ Ｄ．ＢＥ＝ＡＤ ９．据资料，我国古代数学家祖冲之和他的儿子发展 了刘徽的“割圆术”（即圆的内接正多边形边数不 断增加，它的周长就越接近圆周长），他们从圆内 接正六边形算起，一直算到内接正 ２４５７６边形，将 圆周率精确到小数点后七位，使中国对圆周率的 计算在世界上领先了一千多年，依据“割圆术”，由 圆内接正六边形算得的圆周率的近似值是 （　　） Ａ．２．９ Ｂ．３ Ｃ．３．１ Ｄ．３．１４ １０．已知点 Ｍ（ｎ，－ｎ）在第二象限，过点 Ｍ的直线 ｙ ＝ｋｘ＋ｂ（０＜ｋ＜１）分别交 ｘ轴、ｙ轴于点 Ａ，Ｂ， 过点 Ｍ作 ＭＮ⊥ｘ轴于点 Ｎ，则下列点在线段 ＡＮ 的是 （　　） Ａ．（（ｋ－１）ｎ，０） Ｂ．（（ｋ＋３ ２）ｎ，０） Ｃ．（（ｋ＋２）ｎ ｋ ，０） Ｄ．（（ｋ＋１）ｎ，０） 二、填空题（本大题有 ６小题，每小题 ４分，共 ２４分） １１．已知 ｘ＝１是方程 ｘ２－ａ＝０的根，则 ａ＝　　　． １２．一个不透明盒子里装有 ４个除颜色外无其他任 何差别的球，从盒子中随机摸出一个球，若 Ｐ（摸 出红球）＝１ ４，则盒子里有　　　　个红球． １３．如图，已知 ＡＢ＝３，ＡＣ＝１，∠Ｄ＝９０°，△ＤＥＣ与 △ＡＢＣ关 于 点 Ｃ成 中 心 对 称，则 ＡＥ 的 长 是 　　　　　． 第 １３题图 １４．某二次函数的几组对应值如下表所示，若 ｘ１ ＜ｘ２ ＜ｘ３ ＜ｘ４ ＜ｘ５，则 该 函 数 图 象 的 开 口 方 向 是　　　　． ｘ ｘ１ ｘ２ ｘ３ ｘ４ ｘ５ ｙ －３ －５ ４ ０ ２ －１ １５．Ｐ是直线 ｌ上的任意一点，点 Ａ在⊙Ｏ上，设                                                                ＯＰ ４ 的最小值为 ｍ，若直线 ｌ过点 Ａ，则 ｍ与 ＯＡ的大 小关系是　　　　 ． １６．某小学举办“慈善一日捐”演出，共有 ６００张演出 票，成人票价为 ６０元，学生票价为 ２０元，演出票 虽未售完，但售票收入达 ２２０８０元，设成人票售 出 ｘ张，则 ｘ的取值范围是　　　　 ． 三、解答题（本大题有 ９小题，共 ８６分） １７．（本小题满分 ８分）ｘ２ －４ｘ＝１． １８．（本小题满分 ８分）如图，已知 △ＡＢＣ和 △ＤＥＦ 的边 ＡＣ、ＤＦ在一条直线上，ＡＢ∥ ＤＥ，ＡＢ＝ＤＥ， ＡＤ＝ＣＦ，证明：ＢＣ∥ ＥＦ． 第 １８题图 １９．（本小题满分 ８分）如图，已知二次函数图象的顶 点为 Ｐ，与 ｙ轴交于点 Ａ． （１）在图中再确定该函数图象上的一个点 Ｂ并 画出； （２）若 Ｐ（１，３），Ａ（０，２），求该函数的解析式． 第 １９题图 ２０．（本小题满分 ８分）如图，在四边形 ＡＢＣＤ中，ＡＢ ＝ＢＣ，∠ＡＢＣ＝６０°，Ｅ是 ＣＤ边上一点，连接 ＢＥ， 以 ＢＥ为一边作等边三角形 ＢＥＦ，请用直尺在图 中连接一条线段，使图中存在经过旋转可完全重 合的两个三角形，并说明这两个三角形经过什么 样的旋转可重合． 第 ２０题图 ２１．（本小题满分 ８分）某市一家园林公司培育出新 品种树苗，为考察这种树苗的移植的成活率，公 司进行了统计，结果如下表所示． 累积移植 总数（棵） １００ ５００ １０００ ２０００ ５０００ １００００ 成活率 ０．９１０ ０．９６８ ０．９４２ ０．９５６ ０．９４７０．９５０ 现该市实施绿化工程，需移植一批这种树苗，若 这批树苗移植后要有 ２８．５万棵成活，则需要一 次性移植多少棵树苗较为合适？请说明理由                                                                       ． ５ ２２．（本小题满分 １０分）已知直线 ｌ１：ｙ＝ｋｘ＋ｂ经过 点 Ａ（－１ ２，０），和点 Ｂ（２，５）． （１）求直线 ｌ１ 与 ｙ轴的交点坐标； （２）若点 Ｃ（ａ，ａ＋２）与点 Ｄ在直线 ｌ１上，过点 Ｄ 的直线 ｌ２与 ｘ轴正半轴交于点 Ｅ，当 ＡＣ＝ＣＤ＝ ＣＥ时，求 ＤＥ的长． ２３．（本小题满分 １１分）阅读下列材料： 我们通过下列步骤估计方程 ２ｘ２ ＋ｘ－２＝０的根 的所在的范围． 第一步：画出函数 ｙ＝２ｘ２ ＋ｘ－２的图象，发现图 象是一条连续不断的曲线，且与 ｘ轴的一个交点 的横坐标在 ０，１之间． 第二步：因为当 ｘ＝０时，ｙ＝－２＜０；当 ｘ＝１时， ｙ＝１＞０，所以可确定方程 ２ｘ２ ＋ｘ－２＝０的一个 根 ｘ１ 所在的范围是 ０＜ｘ１ ＜１． 第三步：通过取 ０和 １的平均数缩小 ｘ１ 所在的范 围；取 ｘ＝０＋１ ２ ＝１ ２，因为当 ｘ＝１ ２时，ｙ＜０，又因 为当 ｘ＝１时，ｙ＞０，所以 １ ２＜ｘ１ ＜１． （１）请仿照第二步，通过运算，验证 ２ｘ２ ＋ｘ－２＝０ 的另一个根 ｘ２所在范围是 －２＜ｘ２ ＜－１； （２）在 －２＜ｘ２ ＜－１的基础上，重复应用第三步 中取平均数的方法，将 ｘ２ 所在范围缩小至 ｍ＜ｘ２ ＜ｎ，使得 ｎ－ｍ≤ １ ４                                                                       ． ６ ２４．（本小题满分 １１分）已知 ＡＢ是半圆 Ｏ的直径，Ｍ， Ｎ是半圆上不与 Ａ，Ｂ重合的两点，且点 Ｎ在 ) ＢＭ上． （１）如图①，ＭＡ＝６，ＭＢ＝８，∠ＮＯＢ＝６０°，求 ＮＢ 的长； （２）如图②，过点 Ｍ 作 ＭＣ⊥ＡＢ于点 Ｃ，点 Ｐ是 ＭＮ的中点，连接 ＭＢ、ＮＡ、ＰＣ，试探究∠ＭＣＰ、 ∠ＮＡＢ、∠ＭＢＡ之间的数量关系，并证明． 图① 　　 图② 第 ２４题图 ２５．（本小题满分 １４分）在平面直角坐标系中，已知 点 Ａ在抛物线 ｙ＝ｘ２ ＋ｂｘ＋ｃ（ｂ＞０）上，且 Ａ（１， －１）． （１）若 ｂ－ｃ＝４，求 ｂ，ｃ的值； （２）若该抛物线与 ｙ轴交于点 Ｂ，其对称轴与 ｘ 轴交于点 Ｃ，则命题“对于任意一个 ｋ（０＜ｋ＜１）， 都存在 ｂ，使得 ＯＣ＝ｋ·ＯＢ”是否正确？若正确， 请证明；若不正确，请举反例； （３）将该抛物线平移，平移后的抛物线仍经过点 Ａ（１，－１），点 Ａ的对应点 Ａ１ 为（１－ｍ，２ｂ－１）， 当 ｍ≥ －３ ２时，求平移后抛物线的顶点所能达到 的最高点的坐标                                                                       ． ７ ２０１７－２０１８学年福建省泉州市九年级（上）期末 数学试卷 （满分：１５０分　考试时间：１２０分钟） 　　　　　　　　　　　　　　　　　　一、选择题：本题共 １０小题，每小题 ４分，共 ４０分．在 每小题给出的四个选项中，只有一项是符合题目要 求的． １．若二次根式 ｘ槡 －１有意义，则 ｘ的取值范围是 （　　） Ａ．ｘ＞１ Ｂ．ｘ≥１ Ｃ．ｘ≠１ Ｄ．ｘ≤１ ２．下列根式是最简二次根式的是 （　　） 槡Ａ． ２２ Ｂ． ０．槡 ２ 槡Ｃ． １２ Ｄ．槡１ ２ ３．若 ｂ ａ＝２ ５，则ａ－ｂ ａ＋ｂ的值为 （　　） Ａ．１ ４ Ｂ．３ ７ Ｃ．３ ５ Ｄ．７ ３ ４．方程 ｘ２ －２５＝０的解是 （　　） Ａ．ｘ＝５ Ｂ．ｘ１ ＝０，ｘ２ ＝２５ Ｃ．ｘ１ ＝ｘ２ ＝５ Ｄ．ｘ１ ＝５，ｘ２ ＝－５ ５．下列事件为必然事件的是 （　　） Ａ．掷一枚普通的正方体骰子，掷得的点数不小 于 １ Ｂ．任意购买一张电影票，座位号是奇数 Ｃ．抛一枚普通的硬币，正面朝上 Ｄ．一年有 ３６７天 ６．两个相似三角形的对应边的比为 ４∶９，则它们的面 积比为 （　　） Ａ．２∶３ Ｂ．９∶４ Ｃ．１６∶８１ Ｄ．８１∶１６ ７．如图，在△ＡＢＣ中，Ｄ，Ｅ分别是 ＢＣ，ＡＣ的中点，ＡＤ 和 ＢＥ相交于点 Ｇ，若 ＡＤ＝６，则 ＡＧ的长度为 （　　） 第 ７题图 Ａ．２ Ｂ．３ Ｃ．４ Ｄ．５ ８．共享单车为市民出行带来了方便，某单车公司第 一个月投放 １０００辆单车，计划第三个月投放单车 数量比第一个月多 ４４０辆．设该公司第二、三两个 月投放单车数量的月平均增长率为 ｘ，则所列方程 正确的为 （　　） Ａ．１０００（１＋ｘ）＝１４４０ Ｂ．１０００（１＋ｘ）２ ＝４４０ Ｃ．１４４０（１－ｘ）２ ＝１０００ Ｄ．１０００（１＋ｘ）２ ＝１４４０ ９．如图，ＡＢ∥ＣＤ∥ＥＦ，直线 ｌ１，ｌ２分别与这三条平行 线交于点 Ａ，Ｃ，Ｅ和点 Ｂ，Ｄ，Ｆ，则下列式子不一定 成立的是 （　　） 第 ９题图 Ａ．ＡＣ ＣＥ＝ＢＤ ＤＦ Ｂ．ＢＤ ＡＣ＝ＤＦ ＣＥ Ｃ．ＡＣ ＡＥ＝ＢＤ ＢＦ Ｄ．ＡＥ ＡＣ＝ＥＦ ＣＤ １０．对于任意锐角 α，下列结论正确的是 （　　） Ａ．ｓｉｎα＜ｔａｎα Ｂ．ｓｉｎα≤ｔａｎα Ｃ．ｓｉｎα＞ｔａｎα Ｄ．ｓｉｎα≥ｔａｎα 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分． １１．点 （３，－２）关 于 原 点 的 对 称 点 的 坐 标 为 　　　　． １２．计算：（槡３＋１）（槡３－１）＝　　　　． １３．某斜坡的坡度为 ｉ 槡＝１∶３，则这个斜坡的坡角的 度数是　　　　． １４．在一个不透明的袋子中，装有 １个红球和 ２个白 球，这些球除颜色外其余都相同．搅均后从中随 机一次摸出两个球，则摸到的两个球都是白球的 概率是　　　　． １５．我国古代数学著作《九章算术》中有“井深几何” 问题如下；“今有井径五尺，不知其深，立五尺木 于井上，从木末望水岸，入径四寸，问井深几何？” 它的题 意 可 以 由 如 图 所 示 获 得，井 深 ＢＣ为 　　　　尺． 第 １５题图 １６．关于 ｘ的一元二次方程 ａｘ２ ＋ｂｘ＝０（ａ≠０）的一 根为 ｘ＝２０１８，则关于 ｘ的方程 ａ（ｘ＋２）２ ＋ｂｘ                                                                ＋ ８ ２ｂ＝０的根为　　　　． 三、解答题：本题共 ９小题，共 ８６分．解答应写出文字 说明，证明过程或演算步骤． １７．（８分）计算：槡 槡 槡 槡２× ３－ ２４＋｜－ ６｜． １８．（８分）方程 ｘ２ －４ｘ＋（１－ｍ）＝０是关于 ｘ的一 元二次方程． （１）若 ｘ＝４是方程的一个实数根，试求 ｍ的值； （２）若该方程有两个不相等的实数根，试求 ｍ的 取值范围． １９．（８分）如图，在 １１×１４的网格图中，△ＡＢＣ三个 顶点坐标分别为 Ａ（－４，１），Ｂ（－１，１），（－２，４）． （１）以 Ａ为位似中心，将△ＡＢＣ放大为原来的 ２ 倍得到△ＡＢ１Ｃ１，请在网格图中画出△ＡＢ１Ｃ１； （２）直接写出（１）中点 Ｂ１，Ｃ１的坐标． 第 １９题图 ２０．（８分）如图，小亮站在自家阳台上 Ａ处观测到对 面大楼底部 Ｃ的俯角为 ４３°，若两栋楼之间的距 离 ＢＣ为 ３０米，则 Ａ处到地面 Ｂ处的距离 ＡＢ为 多少米？（结果精确到 ０．１米）（供选用数据： ｓｉｎ４３°≈ ０．６８２０，ｃｏｓ４３°≈ ０．７３１４，ｔａｎ４３°≈ ０．９３２５） 第 ２０题图 ２１．（８分）绿苑小区在规划设计时，设置了一块面积 为 ３７５平方米的矩形绿地，并且长比宽多 １０米， 那么绿地的长和宽各为多少米                                                                       ？ ９ ２２．（１０分）在不透明的袋子中有黑棋子 １０枚和白棋 子若干（它们除颜色外都相同），现随机从中摸出 １０枚记下颜色后放回，这样连续做了 １０次，记录 了如下的数据： 次数 １ ２ ３ ４ ５ ６ ７ ８ ９ １０ 黑棋 数 ２ ５ １ ５ ４ ７ ４ ３ ３ ６ 根据以上数据，解答下列问题： （１）直接填空：第 １０次摸棋子摸到黑棋子的频率 为　　　　； （２）试估算袋中的白棋子数量． ２３．（１０分）已知方程 ａｘ２ ＋ｂｘ＋ｃ＝０（ａ≠０）是关于 ｘ 的一元二次方程． （１）直接写出方程根的判别式为　　　　； （２）写出求根公式的推导过程． ２４．（１２分）如图，在矩形 ＡＢＣＤ中，ＣＤ＝４，Ｐ是射线 ＤＡ上的一个动点，连接 ＰＣ，点 Ｄ关于 ＰＣ的对称 点为 Ｅ，连接 ＤＥ交 ＰＣ于点 Ｍ，过点 Ｅ作 ＥＦ⊥ ＤＥ交射线 ＤＡ于点 Ｆ． （１）求证：ＰＤ＝ＰＦ； （２）若 ＤＰ∶ＰＡ＝２∶１，当点 Ｅ落在射线 ＡＢ上时， 求 ＡＥ的长． 第 ２４题图 ２５．（１４分）已知一次函数 ｙ＝ｋｘ 槡－２ ３的图象与 ｘ轴 交于点 Ａ（－２，０），与 ｙ轴交于点 Ｂ，点 Ｐ的坐标 为（０，ｍ）． （１）求 ｋ的值； （２）当 ｍ为何值时，△ＰＯＡ∽△ＡＯＢ？ （３）求槡２ＰＡ＋ＰＢ的最小值                                                                       ． ０１ ２０１７－２０１８学年福建省漳州市九年级（上）期末 数学试卷 （满分：１５０分；考试时间：１２０分钟） 　　　　　　　　　　　　　　　　　　一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分． 每小题只有一个正确选项） １．化简 （－３）槡 ２的结果为 （　　） Ａ．３ Ｂ．－３ Ｃ．±３ Ｄ．９ ２．下列说法中，正确的是 （　　） Ａ．概率很小的事件不可能发生 Ｂ．随机事件发生的概率为 １ ２ Ｃ．必然事件发生的概率是 １ Ｄ．投掷一枚普通硬币 １０次，正面朝上的次数一定 为 ５次 ３．下列计算错误的是 （　　） 槡 槡 槡 槡 槡 槡Ａ． ２＋ ３＝ ５ Ｂ． ２× ３＝ ６ 槡 槡Ｃ． １８÷ ２＝３ Ｄ．（ 槡２ ２）２ ＝８ ４．下列四条线段能成比例线段的是 （　　） Ａ．１，１，２，３ Ｂ．１，２，３，４ Ｃ．２，２，３，３ Ｄ．２，３，４，５ ５．用配方法解方程 ｘ２ －６ｘ＝３，配方正确的是 （　　） Ａ．（ｘ－３）２ ＝０ Ｂ．（ｘ－３）２ ＝６ Ｃ．（ｘ－３）２ ＝９ Ｄ．（ｘ－３）２ ＝１２ ６．在关于 ｘ的一元二次方程 ａｘ２ －３ｘ＝ｂ中，若 ａ与 ｂ 同号，则方程根的情况是 （　　） Ａ．有两个相等的实数根 Ｂ．有两个不相等的实数根 Ｃ．没有实数根 Ｄ．无法判断 ７．如图，△ＡＢＣ的顶点都在正方形网格的格点上，则 ｔａｎ∠ＢＡＣ的值为 （　　） 第 ７题图 Ａ．２ Ｂ．１ ２ Ｃ．槡５ ５ Ｄ．槡１０ １０ ８．关于 ｘ的方程（ｘ＋１）２ －ｍ＝０（其中 ｍ≥０）的解为 （　　） Ａ．ｘ＝－１＋ｍ Ｂ．ｘ＝－１＋槡ｍ Ｃ．ｘ＝－１±ｍ Ｄ．ｘ＝－１±槡ｍ ９．在△ＡＢＣ中，若 ｓｉｎＡ＝槡２ ２，ｔａｎＢ 槡＝ ３，则这个三角形 是 （　　） Ａ．锐角三角形 Ｂ．直角三角形 Ｃ．钝角三角形 Ｄ．等腰三角形 １０．如图，在△ＡＢＣ中，∠ＢＡＣ＝９０°，ＡＢ＝８ｃｍ，ＡＣ＝６ ｃｍ，动点 Ｐ从点 Ｃ出发沿 ＣＢ方向以 ３ｃｍ／ｓ的速 度向点 Ｂ运动，同时动点 Ｑ从点 Ｂ出发沿 ＢＡ方 向以 ２ｃｍ／ｓ的速度向点 Ａ运动，将△ＡＰＱ沿直线 ＡＢ翻折得△ＡＰ′Ｑ，若四边形 ＡＰＱＰ′为菱形，则运 动时间为 （　　） 第 １０题图 Ａ．１ｓ Ｂ．１ ２ ｓ Ｃ．４０ １７ｓ Ｄ．２０ １７ｓ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．比较大小： 槡 槡－２ １１　　　　 －３ ５．（用符号“＞， ＝，＜”填空） １２．若关于 ｘ的一元二次方程 ｘ２ ＋２ｘ＋ａ２ －３＝０有 一根是 ０，则另一根是　　　　． １３．如图，把正六边形转盘 ６等分，其中 ３个等边三角 形涂有阴影，任意转动指针，则指针落在阴影区 域内的概率是　　　　． 第 １３题图 　　　　 第 １４题图 １４．如图，△ＡＢＣ中，点 Ｄ、Ｅ分别是 ＡＢ、ＡＣ边上的 点，欲使△ＡＤＥ∽△ＡＣＢ，则需添加的一个条件是 　　　　．（只写一种情况即可） １５．某型号的手机经过两次降价，售价由原来的 １３２０ 元降为 ６６０元，求每次平均降价的百分率 ｘ，则可 列出方程为　　　　　　　　． 第 １６题图 １６．将一副三角尺按如图所示叠放在一起，若 ＡＢ＝ １２，则阴影部分的面积是　　　　                                                               ． １１ 三、解答题（本大题共 ９小题，满分 ８６分．） １７．（８分）计算下列各题： （１）槡２７＋３槡１ ３ 槡－ １２； （２）（槡３－２）（ 槡２＋ ３）． １８．（８分）解下列方程： （１）２ｘ２ －５ｘ＝０； （２）ｘ２ 槡－２ ３ｘ＝－３． １９．（８分）试探究关于 ｘ的方程 ｘ２ －ｍｘ＋ｍ－２＝０ 的根的情况．（ｍ为实数） ２０．（８分）如图，在△ＡＢＣ中，∠Ａ＝９０°，ＢＣ边上的高 为 ＡＤ． （１）用尺规作图画出 ＡＤ（保留作图痕迹，不写作 法，画完后用黑色签字笔描黑）； （２）求证：ＡＤ２ ＝ＢＤ·ＣＤ． 第 ２０题图 ２１．（８分）如图是有桩公共自行车“达达通”车桩的 截面示意图，点 Ｂ、Ｃ在 ＥＦ上，ＥＦ∥ＨＧ，ＥＨ⊥ＨＧ， ＥＨ＝４ｃｍ，ＡＢ＝９０ｃｍ，∠ＡＢＣ＝７５°，求点 Ａ到地 面的距离 （结果精确到 ０．１ｃｍ）．（参 考 数据： ｓｉｎ７５°≈０．９６６，ｃｏｓ７５°≈０．２５９，ｔａｎ７５°≈３．７３２） 　　 第 ２１题图                                                                       ２１ ２２．（１０分）某班联欢会进入抽奖环节，每位同学都 有一次抽奖机会，抽奖方案为：在四张完全相同 的卡片中分别写上数字 １、２、３、４，从中随机抽取 两张，记录两张卡片上的数字后放回，完成一次 抽奖，记抽出的两张卡片上数字之积为 ａ，对应奖 次如表：用画树状图或列表的方法说明获几等奖 的概率最大． 一等奖 二等奖 三等奖 ａ≥１０ ４＜ａ＜１０ ａ≤４ ２３．（１０分）一条长 ５６ｃｍ的铁丝被剪成两段，每段均 折成正方形，若两个正方形的面积和等于 １００ ｃｍ２，求这两个正方形的边长． 第 ２３题图 ２４．（１２分）在△ＡＢＣ中，ＡＢ＝ＡＣ，∠ＢＡＣ＝α，点 Ｄ、Ｅ 分别在边 ＡＢ、ＢＣ上，连接 ＤＥ，且 ＤＢ＝ＤＥ． （１）如图①，若 α＝９０°，则ＣＥ ＡＤ的值是　　　　； （２）若 α＝１２０°，将△ＢＤＥ绕点 Ｂ按顺时针旋转 到如图②所示的位置，求ＣＥ ＡＤ的值； （３）对于任意角 α，将△ＢＤＥ绕点 Ｂ旋转到如图 ③所示的位置，直接写出 ＣＥ ＡＤ的值为　 　 　　． （用含 α的式子表示） 图① 　 图② 图③ 第 ２４题图 ２５．（１４分）如图，∠ＡＣＢ＝９０°，Ａ（３，０），Ｃ（－１，０）， ＡＢ＝５． （１）ＢＣ的长为　　　　； （２）已知点 Ｄ在 ｘ轴上（不与点 Ｃ重合），连接 ＤＢ，若△ＡＤＢ与△ＡＢＣ相似，求点 Ｄ的坐标； （３）在（２）的条件下，点 Ｐ、Ｑ分别是 ＡＤ和 ＡＢ上 的动点，连接 ＰＱ，设 ＡＰ＝ＢＱ＝ｋ，是否存在 ｋ的 值，使△ＡＰＱ与△ＡＤＢ相似？若存在，请求出 ｋ 的值；若不存在，请说明理由． 第 ２５题图 　 备用图                                                                       ３１ ２０１７－２０１８学年福建省宁德市九年级（上） 期末数学试卷 （满分：１５０分；考试时间：１２０分钟） 　　　　　　　　　　　　　　　　　　一、选 择 题 （本 大 题 共 １０小 题，每 小 题 ４分，共 ４０分．） １．若 ａ ｂ＝５ ２，则ａ－ｂ ｂ ＝ （　　） Ａ．２ ３ Ｂ．３ ２ Ｃ．３ Ｄ．７ ２ ２．已知反比例函数 ｙ＝ｋ ｘ，当 ｘ＞０时，ｙ随 ｘ的增大 而增大，则函数 ｙ＝ｋ ｘ的图象在 （　　） Ａ．第一、三象限 Ｂ．第一、四象限 Ｃ．第二、四象限 Ｄ．第二、三象限 ３．已知一个几何体及其左视图如图所示，则该几何 体的主视图是 （　　） 第 ３题图 ４．把一元二次方程 ｘ２ －６ｘ＋１＝０配方成（ｘ＋ｍ）２ ＝ ｎ的形式，正确的是 （　　） Ａ．（ｘ＋３）２ ＝１０ Ｂ．（ｘ－３）２ ＝１０ Ｃ．（ｘ＋３）２ ＝８ Ｄ．（ｘ－３）２ ＝８ ５．下列图形中△ＡＢＣ∽△ＤＥＦ，则这两个三角形不是 位似图形的是 （　　） ６．若关于 ｘ的一元二次方程 ｘ２ －２ｘ＋ｍ＝０有两个不 相等的实数根，则 ｍ的值可能是 （　　） Ａ．－１ Ｂ．１ Ｃ．３ Ｄ．５ ７．如图，点 Ｐ（ｘ，ｙ）（ｘ＞０，ｙ＞０）在半径为 １的圆上， 则 ｃｏｓα＝ （　　） 第 ７题图 Ａ．ｘ Ｂ．ｙ Ｃ． ｘ ｙ Ｄ．ｙ ｘ ８．下列关于抛物线 ｙ＝－（ｘ－５）２ ＋２有关性质的说 法，错误的是 （　　） Ａ．对称轴是直线 ｘ＝５ Ｂ．开口向下 Ｃ．与 ｘ轴有交点 Ｄ．最小值是 ２ ９．如图，一架梯子斜靠在墙上，设梯子 ＡＢ的中点为 Ｏ，ＡＢ＝６米，ＢＣ＝２米，若梯子 Ｂ端沿地面向右滑 行 １米，则点 Ｏ到点 Ｃ的距离 （　　） Ａ．减小 １米 Ｂ．增大 １米 Ｃ．始终是 ２米 Ｄ．始终是 ３米 第 ９题图 　　　 第 １０题图 １０．如图，在矩形 ＡＢＣＤ中，Ｅ是 ＣＤ边的中点，且 ＢＥ ⊥ＡＣ于点 Ｆ，连接 ＤＦ，则下列结论错误的是 （　　） Ａ．△ＡＤＣ∽△ＣＦＢ Ｂ．ＡＤ＝ＤＦ Ｃ．ＢＣ ＡＣ＝槡３ ２ Ｄ．Ｓ△ＣＥＦ Ｓ△ＡＢＦ ＝１ ４ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分．） １１．计算：２ｓｉｎ６０°＝　　　　． １２．两根不一样长的木杆垂直竖立在地面上，若它们 的影长相等，则此时的投影是　　　　．（填写 “平行投影”或“中心投影”） １３．在不透明的袋子中有红球、黄球共 ４０个，除颜色 外其他完全相同．将袋中的球搅匀，从中随机摸 出一个球，记下颜色后再放回袋中，不断重复这 一过程，摸了 １００次后，发现有 ３０次摸到红球，则 口袋中红球的个数大约是　　　　． １４．将抛物线 ｙ＝２ｘ２向上平移 ３个单位，所得抛物线 的表达式为　　　　． １５．如图，直角三角形纸片 ＡＢＣ，ＡＣ边长为 １０ｃｍ，现 从下往上依次裁剪宽为 ４ｃｍ的矩形纸条，若剪 得第二张矩形纸条恰好是正方形，那么 ＢＣ的长 度是　　　　ｃｍ                                                               ． ４１ 第 １５题图 　　 第 １６题图 １６．如图，点 Ａ，Ｂ在反比例函数 ｙ＝ｋ ｘ的图象上，且直 线 ＡＢ经过原点，点 Ｃ在 ｙ轴正半轴上，直线 ＣＡ 交 ｘ轴于点 Ｅ，直线 ＣＢ交 ｘ轴于点 Ｆ，若ＡＣ ＡＥ＝３， 则ＢＦ ＣＦ＝　　　　． 三、解答题（本大题有 ９小题，共 ８６分．） １７．（８分）如图，Ｄ，Ｅ分别为△ＡＢＣ边 ＡＢ，ＡＣ上的 点，且 ＤＥ∥ＢＣ，若 ＡＤ＝５，ＡＢ＝１５，ＡＥ＝３，求 ＡＣ 的长． 第 １７题图 １８．（８分）已知关于 ｘ的一元二次方程 ｘ２ －４ｘ＋ｃ＝０ 有一个根是 ｘ＝３，求 ｃ与另一个根． １９．（８分）贴春联是中华民族的传统文化．不识字的 王爷爷不小心将两幅对联弄混了，已知这四张联 纸上的文字分别是：①天涯若比邻，②修业勤为 贵，③行文意必高，④海内存知己．若他任意取出 两张联纸，求这两张联纸恰好组成一副对联的 概率． ２０．（９分）如图，点 Ａ（５，２），Ｂ（ｍ，ｎ）（ｍ＜５）在反比 例函数 ｙ＝ ｋ ｘ的图象上，作 ＡＣ⊥ｙ轴于点 Ｃ，连 接 ＢＣ． （１）求反比例函数的表达式； （２）若△ＡＢＣ的面积为 １０，求点 Ｂ的坐标． 第 ２０题图 ２１．（９分）如图，已知ＡＢＣＤ，点 Ｅ在 ＢＣ上，点 Ｆ在 ＡＤ上． （１）请用尺规确定点 Ｅ，Ｆ的位置，使得四边形 ＡＥＣＦ是菱形；（保留作图痕迹，不写作法） （２）利用（１）中作图所确定的条件证明四边形 ＡＥＣＦ是菱形． 第 ２１题图 ２２．（９分）如图是小明阁楼储藏室的侧面示意图，现 他有一个棱长为 １．１ｍ的正方体包裹，                                                                       请通过计 ５１ 算判断，该包裹能否平放入这个储藏室．（参考数 据：ｓｉｎ３１°≈０．５２，ｃｏｓ３１°≈０．８６，ｔａｎ３１°≈０．６０） 第 ２２题图 ２３．（１１分）万达大厦销售某种 Ｔ恤，平均每天可销 售 ４０件，每件盈利 ２０元．为尽量减小库存，提高 日盈利，商场决定采取适当的降价措施．经调查 发现，若该种 Ｔ恤每件降价 ｘ元，则每天的销售 量 ｙ（件）与 ｘ之间的关系如图①所示，每天销售 该种 Ｔ恤的日盈利额 Ｓ（元）与 ｘ之间的关系如图 ②所示． （１）当 Ｔ恤降价 ｘ元时，每件 Ｔ恤盈利　　　　 元，商场日销售量为　　　　件；（用含 ｘ的代数 式表示） （２）若商场计划销售该种 Ｔ恤的日盈利达到 ９００ 元，求每件 Ｔ恤应降价多少元？ （３）直接写出图②中顶点 Ａ的坐标，并说明点 Ａ 的实际意义． 图① 　 图② 第 ２３题图 ２４．（１１分）如图，已知正方形 ＡＢＣＤ，点 Ｅ在 ＢＣ上， 点 Ｆ在 ＣＤ的延长线上，ＢＥ＝ＤＦ． （１）求证：ＡＥ＝ＡＦ； （２）若 ＢＤ与 ＥＦ交于点 Ｍ，连接 ＡＭ，试判断 ＡＭ 与 ＥＦ的数量与位置关系，并说明理由． 第 ２４题图 ２５．（１３分）如图，二次函数 ｙ＝－ｘ２ ＋ｂｘ＋ｃ的图象 与 ｘ轴交于 Ａ，Ｂ两点（点 Ａ在点 Ｂ的左边），顶点 为 Ｐ． （１）若 ｂ＝６，ｃ＝－５，求 Ａ，Ｂ两点的坐标； （２）过点 Ｐ作 ＰＥ⊥ｙ轴于点 Ｅ，若点 Ａ的坐标为 （１，０），且四边形 ＡＢＰＥ是平 行 四 边形，求 ｂ，ｃ 的值； （３）若 ｂ＝７，且点 Ａ，Ｂ在点（１，０）与点（５，０）之 间，求 ｃ的取值范围． 第 ２５题图                                                                       ６１ ２０１７－２０１８学年福建省龙岩市上杭县九年级（上） 期末数学试卷 （满分：１５０分；考试时间：１２０分钟） 　　　　　　　　　　　　　　　　　　一、选择题：本题共 １０小题，每小题 ４分，共 ４０分，在 每小题给出的四个选项中，只有一项是符合题目要 求的． １．下列事件中，是必然事件的是 （　　） Ａ．明天太阳从东方升起 Ｂ．随意翻到一本书的某页，这页的页码是奇数 Ｃ．射击运动员射击一次，命中靶心 Ｄ．经过有交通信号灯的路口，遇到红灯 ２．下列函数中，ｙ是 ｘ的反比例函数的是 （　　） Ａ．ｙ＝３ｘ Ｂ．ｙ＝３ ｘ Ｃ．ｘ２ ３ Ｄ．ｙ＝ ３ ｘ＋１ ３．把抛物线 ｙ＝ｘ２向上平移 １个单位长度得到的抛物 线的表达式为 （　　） Ａ．ｙ＝ｘ２ ＋１ Ｂ．ｙ＝ｘ２ －１ Ｃ．ｙ＝－ｘ２ ＋１ Ｄ．ｙ＝－ｘ２ －１ ４．⊙Ｏ的半径为 ４，点 Ｐ到圆心 Ｏ的距离为 ｄ，如果 点 Ｐ在圆内，则 ｄ （　　） Ａ．ｄ＜４ Ｂ．ｄ＝４ Ｃ．ｄ＞４ Ｄ．０≤ｄ＜４ ５．一元二次方程 ｘ２ ＋３ｘ＋５＝０的根的情况是 （　　） Ａ．有两个不相等的实数根 Ｂ．有两个相等的实数根 Ｃ．没有实数根 Ｄ．无法判断 ６．在正三角形、正四边形、正五边形、正六边形、正八 边形这 ５个图形中，既是轴对称图形又是中心对 称图形的有 （　　） Ａ．２个 Ｂ．３个 Ｃ．４个 Ｄ．５个 ７．如图，在△ＡＢＣ中，∠ＢＡＣ＝６５°，将△ＡＢＣ绕点 Ａ 按逆 时 针 旋 转，得 到 △ＡＢ′Ｃ′，若 ＣＣ′∥ ＡＢ，则 ∠ＢＡＢ′＝ （　　） 第 ７题图 Ａ．３５° Ｂ．４０° Ｃ．５０° Ｄ．６５° ８．一个扇形的圆心角是 １２０°，面积为 ３πｃｍ２，那么这 个扇形的半径是 （　　） Ａ．１ｃｍ Ｂ．３ｃｍ Ｃ．６ｃｍ Ｄ．９ｃｍ ９．某校九年级学生毕业时，每个同学都将自己的相 片向全班其他同学各送一张留作纪念，全班共送 了 ２０７０张相片，如果全班有 ｘ名学生，根据题意， 列出方程为 （　　） Ａ．ｘ（ｘ－１）＝２０７０ Ｂ．ｘ（ｘ＋１）＝２０７０ Ｃ．２ｘ（ｘ＋１）＝２０７０ Ｄ．ｘ（ｘ－１） ２ ＝２０７０ １０．已知 Ｐ（ｘ１，１），Ｑ（ｘ２，２）是一个函数图象上的两 个点，其中 ｘ１ ＜ｘ２ ＜０，则这个函数图象可能是 （　　） 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分． １１．抛物线 ｙ＝ｘ２ －ｘ－１与 ｘ轴的公共点的个数是 　　　　． １２．如图，四边形 ＡＢＣＤ内接于⊙Ｏ，若∠ＢＡＤ＝１１０°， 则∠Ｃ的度数是　　　　． 第 １２题图 １３．已知 ｍ是关于 ｘ的方程 ｘ２ －２ｘ－３＝０的一个根， 则 ２ｍ２ －４ｍ＝　　　　． １４．反比例函数 ｙ＝１－ｋ ｘ 的图象经过点（２，３），则 ｋ＝ 　　　　． １５．以正方形 ＡＢＣＤ的对角线 ＡＣ、ＢＤ所在直线为坐 标轴，建立平面直角坐标系，如图所示，已知点 Ａ 的坐标是（ 槡－ ２，０），现将正方形 ＡＢＣＤ绕原点 Ｏ 顺时针旋转 ４５°，则旋转后点 Ｃ的对应点坐标是 　　　　． 第 １５题图 　 第 １６题图 １６．《九章算术》是我国古代内容极为丰富的数学名 著，书中有下列问题“今有勾八步，股十五步，                                                               问 ７１ 勾中容圆，径几何？”其意思是：“如图，今有直角 三角形，勾（短直角边）长为 ８步，股（长直角边） 长为 １５步，问该直角三角形能容纳的圆形（内切 圆）直径是　　　　步． 三、解答题：本题共 ９小题，共 ８６分．解答应写出文字 说明、证明过程或演算步骤． １７．（８分）解方程： （１）２ｘ２ －８＝０； （２）２ｘ２ －４ｘ＝７． １８．（８分）已知函数 ｙ＝ｘ２ －４ｘ＋３． （１）在平面直角坐标系中画出这个函数的图象； （２）观察图象，当 ｘ取何值时，ｙ＞０？ １９．（８分）如 图，一 条 公 路 的 转 弯 处 是 一 段 圆 弧 （ ) ＡＢ）． （１）用直尺和圆规作出 ) ＡＢ所在圆的圆心 Ｏ；（要求 保留作图痕迹，不写作法） （２）若 ) ＡＢ的中点 Ｃ到弦 ＡＢ的距离为 ２０ｍ，ＡＢ＝ ８０ｍ，求 ) ＡＢ所在圆的半径． 第 １９题图 ２０．（８分）如图，等腰直角△ＡＢＣ中，∠ＡＣＢ＝９０°，点 Ｄ在 ＡＢ上，将△ＢＣＤ绕顶点 Ｃ沿顺时针方向旋 转 ９０°后，得到△ＡＣＥ． （１）求∠ＤＡＥ的度数； （２）当 ＡＢ＝４，ＢＤ∶ＤＡ＝１∶３时，求 ＤＥ的长． 第 ２０题图 ２１．（８分）如图，在平面直角坐标系中，反比例函数 ｙ ＝ｋ ｘ（ｘ＞０）的图象上有一点 Ａ（ｍ，２ ３），过点 Ａ 作 ＡＢ⊥ｘ轴于点 Ｂ，将点 Ｂ向左平移 ２个单位长 度得到点 Ｃ，过点 Ｃ作 ｙ轴的平行线交反比例函 数的图象于点 Ｄ，ＣＤ＝２． （１）写出点 Ｄ的横坐标（用含 ｍ的式子表示）； （２）求出反比例函数的解析式． 第 ２１题图                                                                       ８１ ２２．（８分）在学校体育活动时间，小英、小丽、小敏、 小洁四位同学进行一次羽毛球比赛，现要从中选 出两位同学打第一场比赛． （１）如果确定小英打第一场，再从其余三人中随 机选取一人打第一场，求恰好选中小洁的概率； （２）如果让小英做裁判，用“手心手背”的方法决 定其余三人哪两人打第一场．游戏规则是：三人 同时伸“手心手背”中的一种手势，如果恰好两人 伸出的手势相同，那么这两人上场，否则重新开 始．这三人伸出“手心”或“手背”都是随机的，请 用画树状图的方法，求小丽和小敏打第一场的 概率． ２３．（１２分）如图，用一段长为 ４０ｍ的篱笆围成一个 一边靠墙的矩形花圃 ＡＢＣＤ，墙长 ２４ｍ．设 ＡＢ长 为 ｘｍ，矩形的面积为 Ｓｍ２． （１）写出 Ｓ与 ｘ的函数关系式； （２）当 ＡＢ长为多少米时，所围成的花圃面积最 大？最大值是多少？ （３）当花圃的面积为 １５０ｍ２时，ＡＢ长为多少米？ 第 ２３题图 ２４．（１２分）四边形 ＡＢＣＤ的对角线交于点 Ｅ，且 ＡＥ＝ ＥＣ，ＢＥ＝ＥＤ，以 ＡＤ为直径的半圆过点 Ｅ，圆心 为 Ｏ． （１）如图①，求证：四边形 ＡＢＣＤ为菱形； （２）如图②，若 ＢＣ的延长线与半圆相切于点 Ｆ， 且直径 ＡＤ＝６，求 ) ＡＥ的长． 图① 图② 第 ２４题图 ２５．（１４分）已知抛物线 ｙ＝ｘ２ ＋ｂｘ＋ｃ． （１）抛物线经过点 Ａ（－１，０），Ｂ（２，－３），求该抛 物线的解析式和顶点坐标； （２）在（１）的条件下，设 Ｐ（ｓ，ｔ）为抛物线上的一 个动点，Ｐ关于原点的对称点为 Ｐ′，若点 Ｐ′恰好 落在该抛物线上，求 ｓ的值； （３）点 Ｍ（ｍ，ｎ），Ｎ（ｍ＋２，１ ７ｎ），Ｑ（ｍ＋８，ｎ）在抛 物线 ｙ＝ｘ２ ＋ｂｘ＋ｃ上，求△ＭＮＱ的面积                                                                       ． ９１ ２０１７－２０１８学年南平市九年级（上）期末 数学试卷 （满分：１５０分　考试时间：１２０分钟） 　　　　　　　　　　　　　　　　　　一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分． 每小题只有一个正确的选项．） １．在平面直角坐标系中，点 Ｍ（１，－２）与点 Ｎ关于原 点对称，则点 Ｎ的坐标为 （　　） Ａ．（－２，１） Ｂ．（１，－２） Ｃ．（２，－１） Ｄ．（－１，２） ２．用配方法解一元二次方程 ｘ２ ＋２ｘ－１＝０，可将方 程配方为 （　　） Ａ． ｘ( )＋１２ ＝２ Ｂ． ｘ( )＋１２ ＝０ Ｃ． ｘ( )－１２ ＝２ Ｄ． ｘ( )－１２ ＝０ ３．下列事件中，属于随机事件的有 （　　） ①任意画一个三角形，其内角和为 ３６０°； ②投一枚骰子得到的点数是奇数； ③经过有交通信号灯的路口，遇到红灯； ④从日历本上任选一天为星期天． Ａ．①②③ Ｂ．②③④ Ｃ．①③④ Ｄ．①②④ ４．下列抛物线的顶点坐标为（４，－３）的是 （　　） Ａ．ｙ＝ ｘ( )＋４２ －３ Ｂ．ｙ＝ ｘ( )＋４２ ＋３ Ｃ．ｙ＝ ｘ( )－４２ －３ Ｄ．ｙ＝ ｘ( )－４２ ＋３ ５．有 ｎ支球队参加篮球比赛，共比赛了 １５场，每两个 队之间只比赛一场，则下列方程中符合题意的是 （　　） Ａ．ｎ ｎ( )－１ ＝１５ Ｂ．ｎ ｎ( )＋１ ＝１５ Ｃ．ｎ ｎ( )－１ ＝３０ Ｄ．ｎ ｎ( )＋１ ＝３０ ６．某小组在“用频率估计概率”的实验中，统计了某 种结果出现的频率，绘制了如图所示的折线图，那 么符合这一结果的实验最有可能的是 （　　） 第 ６题图 Ａ．袋子中有 １个红球和 ２个黄球，它们只有颜色 上的区别，从中随机地取出一个球是黄球 Ｂ．掷一个质地均匀的正六面体骰子，落地时面朝 上的点数是 ６ Ｃ．在“石头、剪刀、布”的游戏中，小宇随机出的是 “剪刀” Ｄ．掷一枚质地均匀的硬币，落地时结果是“正面 向上” ７．如果一个正多边形的中心角为 ６０°，那么这个正多 边形的边数是 （　　） Ａ．４ Ｂ．５ Ｃ．６ Ｄ．７ ８．已知点 Ａ（ｘ１，ｙ１），Ｂ（ｘ２，ｙ２）是反比例函数 ｙ＝－１ ｘ 的图象上的两点，若 ｘ１ ＜０＜ｘ２，则下列结论正确的 是 （　　） Ａ．ｙ１ ＜０＜ｙ２ Ｂ．ｙ２ ＜０＜ｙ１ Ｃ．ｙ１ ＜ｙ２ ＜０ Ｄ．ｙ２ ＜ｙ１ ＜０ ９．如图，ＡＢ为⊙Ｏ的直径，ＰＤ切⊙Ｏ于点 Ｃ，交 ＡＢ 的延长线于点 Ｄ，且 ＣＯ＝ＣＤ，则∠ＰＣＡ＝ （　　） Ａ．３０° Ｂ．４５° Ｃ．６０° Ｄ．６７．５° 第 ９题图 　　 第 １０题图 １０．如图，在 Ｒｔ△ＡＢＣ和 Ｒｔ△ＡＢＤ中，∠ＡＤＢ＝∠ＡＣＢ ＝９０°，∠ＢＡＣ＝３０°，ＡＢ＝４，ＡＤ 槡＝２ ２，连接 ＤＣ， 将 Ｒｔ△ＡＢＣ绕点 Ｂ顺时针旋转一周，则线段 ＤＣ 长的取值范围是 （　　） Ａ．２≤ＤＣ≤４ 槡Ｂ．２ ２≤ＤＣ≤４ 槡Ｃ．２ ２－２≤ＤＣ≤ 槡２ ２ 槡Ｄ．２ ２－２≤ＤＣ≤ 槡２ ２＋２ 二、填空题（本大题共 ６小题，每空 ４分，共 ２４分．） １１．如图，在平面直角坐标系 ｘＯｙ中，矩形 ＯＡＢＣ，ＯＡ ＝２，ＯＣ＝１，写出一个函数 ｙ＝ｋ ｘ ｋ≠( )０，使它的 图象与矩形 ＯＡＢＣ的边有两个公共点，这个函数 的表达式可以为　　　　（答案不唯一）． 第 １１题图 １２．已知关于 ｘ的方程 ｘ２＋３ｘ＋ａ＝０有一个根为 －２，ａ ＝　　　　． １３．圆锥的底面半径为 ７ｃｍ，母线长为 １４ｃｍ，则该圆 锥的侧面展开图的圆心角为　　　　°． １４．设 Ｏ为△ＡＢＣ的内心，若∠Ａ＝４８°，则∠ＢＯＣ＝ 　　　　°． １５．把球放在长方体纸盒内，球的一部分露出盒外， 其截面如图所示，已知 ＥＦ＝ＣＤ＝４ｃｍ，                                                               则球的半 ０２ 径为　　　　ｃｍ． 第 １５题图 １６．抛物线 ｙ＝ａｘ２ ＋ｂｘ＋ｃ（ａ＞０）过点（－１，０）和点 （０，－３），且顶点在第四象限，则 ａ的取值范围是 　　　　． 三、解答题（本大题共 ９小题，共 ８６分．） １７．解方程（每小题 ４分，共 ８分） （１）ｘ２ ＋２ｘ＝０；　　　　（２）３ｘ２ ＋２ｘ－１＝０． １８．（８分）已知关于 ｘ的方程 ｋｘ２ ＋（ｋ＋３）ｘ＋３＝０ （ｋ≠０）． （１）求证：方程一定有两个实数根； （２）若方程的两个实数根都是整数，求正整数 ｋ 的值． １９．（８分）有甲、乙两个不透明的布袋，甲袋中有 ３个 完全相同的小球，分别标有数字 ０，１和 ２；乙袋中 有 ３个完全相同的小球，分别标有数字 １，２和 ３， 小明从甲袋中随机取出 １个小球，记录标有的数 字为 ｘ，再从乙袋中随机取出 １个小球，记录标有 的数字为 ｙ，这样确定了点 Ｍ的坐标（ｘ，ｙ）． （１）写出点 Ｍ所有可能的坐标； （２）求点 Ｍ在直线 ｙ＝－ｘ＋３上的概率． ２０．（８分）如图，直线 ｙ＝ｘ＋２与 ｙ轴交于点 Ａ，与反 比例函数 ｙ＝ｋ ｘ ｋ≠( )０的图象交于点 Ｃ，过点 Ｃ 作 ＣＢ⊥ｘ轴于点 Ｂ，ＡＯ＝２ＢＯ，求反比例函数的 解析式． 第 ２０题图 ２１．（８分）如图，１２×１２的正方形网格中的每个小正 方形的边长都是 １，正方形的顶点叫做格点．矩形 ＡＢＣＤ的 四 个 顶 点 Ａ，Ｂ，Ｃ，Ｄ都 在 格 点 上，将 △ＡＤＣ绕点 Ａ顺时针方向旋转得到△ＡＤ′Ｃ′，点 Ｃ与点 Ｃ′为对应点． （１）在 正 方 形 网 格 中 确 定 Ｄ′的 位 置，并 画 出 △ＡＤ′Ｃ′； （２）若边 ＡＢ交边 Ｃ′Ｄ′于点 Ｅ，求 ＡＥ的长． 第 ２１题图                                                                       １２ ２２．（１０分）在矩形 ＡＢＣＤ中，ＡＢ＝８，ＢＣ＝６，将矩形 按图示方式进行分割，其中正方形 ＡＥＦＧ与正方 形 ＪＫＣＩ全等，矩形 ＧＨＩＤ与矩形 ＥＢＫＬ全等． （１）当矩形 ＬＪＨＦ的面积为 ３ ４时，求 ＡＧ的长； （２）当 ＡＧ为何值时，矩形 ＬＪＨＦ的面积最大． 第 ２２题图 ２３．（１０分）如图，点 Ａ，Ｃ，Ｄ，Ｂ在以 Ｏ点为圆心，ＯＡ 长为半径的圆弧上，ＡＣ＝ＣＤ＝ＤＢ，ＡＢ交 ＯＣ于点 Ｅ．求证：ＡＥ＝ＣＤ． 第 ２３题图 ２４．（１２分）如图，在等边△ＢＣＤ中，ＤＦ⊥ＢＣ于点 Ｆ， 点 Ａ为直线 ＤＦ上一动点，以 Ｂ为旋转中心，把 ＢＡ按顺时针方向旋转 ６０°至 ＢＥ，连接 ＥＣ． （１）当点 Ａ在线段 ＤＦ的延长线上时， ①求证：ＤＡ＝ＣＥ； ②判 断 ∠ＤＥＣ和 ∠ＥＤＣ的 数 量 关 系，并 说 明 理由； （２）当∠ＤＥＣ＝４５°时，连接 ＡＣ，求∠ＢＡＣ的度数． 第 ２４题图 ２５．（１４分）如图，在平面直角坐标系 ｘＯｙ中，二次函 数 ｙ＝ａｘ２ ＋ｂｘ＋ｃ（ａ≠０）的图象经过 Ａ（０，４）， Ｂ（２，０），Ｃ（－２，０）三点． （１）求二次函数的解析式； （２）在 ｘ轴上有一点 Ｄ（－４，０），将二次函 数图象沿 ＤＡ方向平移，使图象再次经过点 Ｂ． ①求平移后图象顶点 Ｅ的坐标； ②求图象 Ａ，Ｂ两点间的部分扫过的面积． 第 ２５题图                                                                       ２２ 书书书 １　　　　 ２０１７－２０１８学年福建省福州市九年级（上）期末数学试卷 参考答案 一、选择题 １．Ｃ　２．Ａ　３．Ｂ　４．Ｄ　５．Ｄ　６．Ｂ　７．Ａ　８．Ｃ　９．Ａ １０．Ｄ 二、填空题（共 ６小题，每小题 ４分） １１．ｙ＝６ ｘ　１２．１ ４　１３．三　１４．３００　１５．２　１６．３∶２ 三、解答题 １７．解：ｘ２ －２ｘ＝１， ｘ２ －２ｘ＋１２ ＝１＋１２， （ｘ－１）２ ＝２． ∴ｘ 槡－１＝± ２， ∴ｘ 槡＝１± ２． 即 ｘ１ 槡＝１＋ ２，ｘ２ 槡＝１－ ２． １８．解：ａ＝１，ｂ＝２ｍ＋１，ｃ＝ｍ（ｍ＋１）， ∵Δ＝ｂ２ －４ａｃ ＝（２ｍ＋１）２ －４×１×ｍ（ｍ＋１） ＝４ｍ２ ＋４ｍ＋１－４ｍ２ －４ｍ ＝１＞０， ∴不论实数 ｍ取何值，方程总有实数根． １９．已知：如解图，△ＡＢＣ∽ △Ａ′Ｂ′Ｃ′，相 似 比 为 ｋ，ＡＤ是 △ＡＢＣ的高，Ａ′Ｄ′是△Ａ′Ｂ′Ｃ′的高． 求证：ＡＤ Ａ′Ｄ′＝ｋ． 第 １９题解图 证明： ∵△ＡＢＣ∽△Ａ′Ｂ′Ｃ′， ∴∠Ｂ＝∠Ｂ′， ∵ＡＤ是△ＡＢＣ的高，Ａ′Ｄ′是△Ａ′Ｂ′Ｃ′的高， ∴∠ＡＤＢ＝∠Ａ′Ｄ′Ｂ′＝９０°， ∴△ＡＢＤ∽△Ａ′Ｂ′Ｄ′， ∴ ＡＤ Ａ′Ｄ′＝ＡＢ Ａ′Ｂ′＝ｋ． ２０．解：（１）Ｐ＝９６ Ｖ； （２）当 Ｐ＝１４４时，Ｖ＝２ ３， ∴Ｐ≤１４４时，Ｖ≥ ２ ３， 即气球的体积应不多于 ２ ３立方米． ２１．解：（１）旋转后的三角形 ＡＣＰ′如解图①所示： 第 ２１题解图① （２）如解图②，由旋转的性质可得，∠ＰＡＰ′＝∠ＢＡＣ＝ ５０°，ＡＰ＝ＡＰ′，△ＡＢＰ≌△ＡＣＰ′， ∴∠ＡＰＰ′＝∠ＡＰ′Ｐ＝６５°，∠ＡＰ′Ｃ＝∠ＡＰＢ， ∵∠ＢＡＣ＝５０°，ＡＢ＝ＡＣ， ∴∠Ｂ＝６５°， 又∵∠ＢＡＰ＝２０°， ∴∠ＡＰＢ＝９５°＝∠ＡＰ′Ｃ， ∴∠ＰＰ′Ｃ＝∠ＡＰ′Ｃ－∠ＡＰ′Ｐ＝９５°－６５°＝３０°． 第 ２１题解图② ２２．解：（１）０．２５； （２）由（１）可知，黑棋的个数为 ４×０．２５＝１，则白棋的个 数为 ３， 列表如下： 黑 白１ 白２ 白３ 黑 （白１，黑） （白２，黑） （白３，黑） 白１ （黑，白１） （白２，白１） （白３，白１） 白２ （黑，白２）（白１，白２） （白３，白２） 白３ （黑，白３）（白１，白３）（白２，白３） 由列表可知，所有等可能结果共有 １２种，其中这两枚棋 颜色不同的结果有 ６种， ∴这两枚棋颜色不同的概率为 １ ２． ２３．（１）证明：如解图①，连接 ＡＣ， 第 ２１题解图① ∵ ) ＡＣ＝ ) ＢＤ， ∴ ) ＡＣ－ ) ＣＤ＝ ) ＢＤ－ ) ＣＤ， 即 ) ＡＤ＝ ) ＢＣ， ∴∠ＣＡＢ＝∠ＡＣＤ， ∴ＡＢ∥ＣＥ， ∵ＡＥ⊥ＣＤ， ∴∠ＡＥＣ＝９０°， ∴∠ＥＡＢ＝９０°， ∴ＡＥ⊥ＡＢ， ∵ＯＡ为半圆 Ｏ的半径， ∴ＡＥ与半圆 Ｏ相切； （２）解：如解图②，连接 ＡＤ，ＯＤ， ∵Ｒｔ△ＡＤＥ中，∠ＡＥＤ＝９０°，ＡＥ 槡＝２ ３，ＤＥ＝２， ∴ＡＤ＝ ＡＥ２ ＋ＤＥ槡 ２ ＝４， ∴∠ＥＡＤ＝３０°， ∴∠ＤＡＯ＝６０°， ∵ＯＡ＝ＯＤ                                                                   ， ２　　　　 ∴△ＡＯＤ是等边三角形， ∴∠ＡＯＤ＝６０°，ＯＡ＝ＡＤ＝４， ∴Ｓ阴影 ＝Ｓ四边形ＡＯＤＥ －Ｓ扇形ＯＡＤ ＝ １ ２ ×（２＋４） 槡×２ ３－ ６０π×４２ ３６０ 槡＝６ ３－８π ３． 第 ２３题解图② ２４．解：（１）如解图①，连接 ＣＤ． 第 ２４题解图① 在 Ｒｔ△ＡＢＣ中，∠ＡＣＢ＝９０°，ＡＣ＝ＢＣ＝４， ∴ＡＢ＝ ＡＣ２ ＋ＢＣ槡 ２ 槡＝４ ２， ∵ＡＤ＝ＤＢ， ∴ＣＤ＝１ ２ＡＢ 槡＝２ ２，ＣＤ⊥ＡＢ， 在 Ｒｔ△ＣＤＰ中，ＣＰ＝ ＰＤ２ ＋ＣＤ槡 ２ ＝３； （２）如解图②，∵ＤＰ＝１， ∴点 Ｐ在以点 Ｄ为圆心，ＤＰ长为半径的⊙Ｄ上． 第 ２４题解图② ①当 ＰＢ＝ＰＣ时， ∵ＣＤ＝ＤＢ， ∴Ｐ、Ｄ都在线段 ＢＣ的垂直平分线上，设直线 ＤＰ交 ＢＣ 于点 Ｅ． ∴∠ＰＥＣ＝９０°，ＢＥ＝ＣＥ＝２， ∵∠ＣＤＢ＝９０°， ∴ＤＥ＝１ ２ＢＣ＝ＣＥ＝２， 在 Ｒｔ△ＰＣＥ中，ＰＣ２ ＝ＥＣ２ ＋ＰＥ２， 当点 Ｐ在线段 ＥＤ上时，ＰＥ＝ＤＥ－ＤＰ＝１， ∴ＰＣ＝ １２ ＋２槡 ２ 槡＝ ５， 当 Ｐ在线段 ＥＤ的延长线上时，ＰＥ＝ＥＤ＋ＤＰ＝３， ∴ＰＣ＝ ３２ ＋２槡 ２ 槡＝ １３． ②当 ＰＣ＝ＢＣ时，∵ＰＣ≤ＣＤ＋ＰＤ 槡＝２ ２＋１＜ＢＣ， ∴ＰＣ≠ＢＣ，此种情形不存在； ③如解图③，当 ＰＢ＝ＢＣ时，同理这种情形不存在； 第 ２４题解图③ （３）如解图④，连接 ＢＢ′． 第 ２４题解图④ 由旋转的性质可知：ＰＢ＝ＰＢ′，∠ＢＰＢ′＝９０°， ∴∠ＰＢＢ′＝４５°， ∴ＢＢ′ 槡＝ ２ＰＢ， ∴ＢＰ′ 槡＝ ２， ∵ＡＣ＝ＢＣ，∠ＡＣＢ＝９０°， ∴∠ＡＢＣ＝４５°， ∴∠ＡＢＣ＝∠ＰＢＢ′， ∴∠ＡＢＢ′＝∠ＣＢＰ， ∵ＢＡ ＢＣ＝ 槡４ ２ ４ 槡＝ ２， ∴ＢＡ ＢＣ＝ＢＢ′ ＰＢ， ∴ ＢＡ ＢＢ′＝ＢＣ ＰＢ， ∴△ＡＢＢ′∽△ＣＢＰ， ∴ＡＢ′ ＣＰ＝ＢＡ ＢＣ 槡＝ ２， ∵ＰＣ≤ＣＤ＋ＤＰ 槡＝２ ２＋１， ∴点 Ｐ落在 ＣＤ的延长线与⊙Ｄ的交点处，ＰＣ的值最 大， ∴ＡＢ′≤槡２（ 槡２ ２＋１） 槡＝４＋ ２． ∴ＡＢ′的最大值为 槡４＋ ２． ２５．解：（１）∵二次函数 ｙ＝ａｘ２ ＋ｂｘ＋１ ２（ａ＞０，ｂ＜０）的图象 与 ｘ轴只有一个公共点 Ａ， ∴Δ＝ｂ２ －４ａ×１ ２ ＝ｂ２ －２ａ＝０， ∵ａ＝１ ２， ∴ｂ２ ＝１， ∵ｂ＜０， ∴ｂ＝－１， ∴二次函数的解析式为 ｙ＝１ ２ｘ２ －ｘ＋１ ２， 当 ｙ＝０时，１ ２ｘ２ －ｘ＋１ ２ ＝０，解得 ｘ１ ＝ｘ２ ＝１， ∴Ａ（１，０）； （２）∵ｂ２ ＝２ａ， ∴ａ＝１ ２ｂ２， ∴ｙ＝１ ２ｂ２ｘ２ ＋ｂｘ＋１ ２ ＝１ ２（ｂｘ＋１）２， 当 ｙ＝０时，ｘ＝－１ ｂ， ∴Ａ（－１ ｂ，０）， 将 Ａ代入 ｙ＝ｘ＋ｋ，得到 ｋ＝１ ｂ， 由 ｙ＝１ ２ｂ２ｘ２ ＋ｂｘ＋１ ２ ｙ＝ｘ＋１{ ｂ ，消去 ｙ得到：１ ２ｂ２ｘ２ ＋（ｂ－１）                                                                        ｘ ３　　　　 ＋１ ２ －１ ｂ＝０， 解得 ｘ１ ＝－１ ｂ，ｘ２ ＝２－ｂ ｂ２ ， ∵点 Ａ的横坐标为 －１ ｂ， ∴点 Ｂ的横坐标 ｍ＝２－ｂ ｂ２ ， ∴ｍ＝２－ｂ ｂ２ ＝２×（１ ｂ２ －１ ２ｂ）＝２×（１ ｂ－１ ４）２ －１ ８， ∵２＞０， ∴当 １ ｂ＜１ ４时，ｍ随 １ ｂ的增大而减少， ∵ －１≤ｂ＜０， ∴ １ ｂ≤ －１， ∴ｍ≥２×（－１－１ ４）２ －１ ８ ＝３， 即 ｍ≥３                                                                        ． ４　　　　 ２０１７—２０１８学年厦门市九年级（上）期末 数学试卷参考答案 说明：解答只列出试题的一种或几种解法．如果考生的解法与所列解法不同，可参照评分量表的要求相应评分． 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分） 题号 １ ２ ３ ４ ５ ６ ７ ８ ９ １０ 选项 Ｃ Ａ Ｄ Ａ Ａ Ｄ Ｂ Ｃ Ｂ Ｄ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．１　１２．１　１３．槡１３　１４．向下　１５．ｍ≤ＯＡ １６．２５２＜ｘ≤３６８（ｘ为整数）或 ２５３≤ｘ≤３６８（ｘ为整数） 三、解答题（本大题有 ９小题，共 ８６分） １７．解：由题知，ｘ２ －４ｘ＋４＝５． ４分!!!!!!!!!! 即（ｘ－２）２ ＝５． 由此可得 ｘ 槡－２＝± ５． ６分!!!!!!!!!!!! ∴ｘ１ 槡＝ ５＋２，ｘ２ 槡＝－ ５＋２． ８分!!!!!!!!!! １８．证明：∵ＡＢ∥ＤＥ， ∴∠ＢＡＣ＝∠ＥＤＦ． ２分!!!!!!!!!!!!! ∵ＡＤ＝ＣＦ， ∴ＡＤ＋ＤＣ＝ＣＦ＋ＤＣ． 即 ＡＣ＝ＤＦ． ４分!!!!!!!!!!!!!!!! 又∵ＡＢ＝ＤＥ， ∴△ＡＢＣ≌△ＤＥＦ（ＳＡＳ）． ６分!!!!!!!!!! ∴∠ＢＣＡ＝∠ＥＦＤ． ∴ＢＣ∥ＥＦ． ８分!!!!!!!!!!!!!!!! １９．解：（１）如解图，点 Ｂ即为所求； ３分!!!!!!!! 第 １９题解图 （２）由二次函数图象顶点为 Ｐ（１，３），可设函数的解析式 为 ｙ＝ａ（ｘ－１）２ ＋３． ６分!!!!!!!!!!!! 把 Ａ（０，２）代入，得 ａ＋３＝２． 解得 ａ＝－１． ７分!!!!!!!!!!!!!!! ∴函数的解析式为 ｙ＝－（ｘ－１）２ ＋３． ８分!!!!! ２０．解：如解图，连接 ＡＦ． ３分!!!!!!!!!!!! 第 ２０题解图 　 将△ＣＢＥ绕点 Ｂ逆时针旋转 ６０°，可与△ＡＢＦ重合． ８分!!!!!!!!!!!!!!!!!!!! ２１．解：由表格可知，随着树苗移植数量的增加，树苗移植成 活率越来越稳定．当移植总数为 １００００时，成活率为 ０． ９５０，于是可以估计树苗移植成活率为 ０．９５０． ３分!! 则该市需要购买的树苗数量约为 ２８．５÷０．９５０＝３０（万棵）． 答：该市需向这家园林公司购买约 ３０万棵树苗较为合 适． ８分!!!!!!!!!!!!!!!!!!! ２２．解：（１）把 Ａ（－１ ２，０），Ｂ（２，５）分别代入 ｙ＝ｋｘ＋ｂ中，可 得 ｋ＝２，ｂ＝１，则直线 ｌ１ 的解析式为 ｙ＝２ｘ＋１． ３分 !!! !!!!!!!!!!!!!!!!!!!! 当 ｘ＝０时，ｙ＝１， ∴直线 ｌ１与 ｙ轴的交点坐标为（０，１）； ５分!!!!! （２）如解图，把 Ｃ（ａ，ａ＋２）代入 ｙ＝２ｘ＋１中，可得 ａ＝ １． ６分!!!!!!!!!!!!!!!!!!!! 则点 Ｃ的坐标为（１，３）． ∵ＡＣ＝ＣＤ＝ＣＥ，点 Ｄ在直线 ＡＣ上， ∴点 Ｅ在以线段 ＡＤ为直径的圆上． ∴∠ＤＥＡ＝９０°． ８分!!!!!!!!!!!!!! 过点 Ｃ作 ＣＦ⊥ｘ轴于点 Ｆ， 则 ＣＦ＝ｙＣ ＝３． ９分!!!!!!!!!!!!!!! ∵ＡＣ＝ＣＥ， ∴ＡＦ＝ＥＦ． 又∵ＡＣ＝ＣＤ， ∴ＣＦ是△ＤＥＡ的中位线． ∴ＤＥ＝２ＣＦ＝６． １０分!!!!!!!!!!!!! 第 ２２题解图 ２３．解：（１）∵当 ｘ＝－２时，ｙ＝４＞０；当 ｘ＝－１时，ｙ＝－１＜０， ∴方程 ２ｘ２ ＋ｘ－２＝０的另一个根 ｘ２所在的范围是 －２＜ ｘ２ ＜－１； ４分!!!!!!!!!!!!!!!!! （２）取 ｘ＝（－２）＋（－１） ２ ＝－３ ２， ∴当 ｘ＝－３ ２时，ｙ＝１＞０， 又∵当 ｘ＝－１时，ｙ＝－１＜０， ∴ －３ ２ ＜ｘ２ ＜－１．此时 －１－（－３ ２）＝１ ２ ＞１ ４． ７分 !! !!!!!!!!!!!!!!!!!!!! 继续取 ｘ＝ （－３ ２）＋（－１） ２ ＝－５ ４， ∵当 ｘ＝－５ ４时，ｙ＝－１ ８ ＜０，当 ｘ＝－３ ２时，ｙ＝１＞０， ∴ －３ ２ ＜ｘ２ ＜－５ ４． １０分!!!!!!!!!!!! 又∵ －５ ４ －（－３ ２）＝１ ４， ∴ －３ ２ ＜ｘ２ ＜－５ ４，即为所求 ｘ２的范围． １１分!!! ２４．解：（１）如解图①，连接 ＮＢ，∵ＡＢ是半圆 Ｏ的直径， ∴∠Ｍ＝９０°． １分!!!!!!!!!!!!!!!! 在 Ｒｔ△ＡＭＢ中，ＡＢ＝ ＭＡ２ ＋ＭＢ槡 ２，由于 ＭＡ＝６，ＭＢ＝８， ２分!!!!!!!!!!!!!!!!!!!!! ∴ＡＢ＝１０． ∴ＯＢ＝５． ３分                                                                 !!!!!!!!!!!!!!!!! ５　　　　 ∵ＯＢ＝ＯＮ，∠ＮＯＢ＝６０°， ∴△ＮＯＢ是等边三角形． ４分!!!!!!!!!!! ∴ＮＢ＝ＯＢ＝５； ５分!!!!!!!!!!!!!!! 第 ２４题解图① （２）∠ＭＣＰ＋∠ＭＢＡ＋∠ＮＡＢ＝９０°． 证明如下：如解图②，画⊙Ｏ，延长 ＭＣ交⊙Ｏ于点 Ｑ，连 接 ＮＱ，ＮＢ，ＯＱ，ＯＭ，ＯＮ． 第 ２４题解图② ∵ＭＣ⊥ＡＢ，ＯＭ＝ＯＱ， ∴ＭＣ＝ＣＱ． ６分!!!!!!!!!!!!!!!! 即 Ｃ是 ＭＱ的中点． 又∵Ｐ是 ＭＮ的中点， ∴ＣＰ是△ＭＱＮ的中位线． ８分!!!!!!!!!! ∴ＣＰ∥ＱＮ． ∴∠ＭＣＰ＝∠ＭＱＮ． ∵∠ＭＱＮ＝１ ２∠ＭＯＮ，∠ＭＢＮ＝１ ２∠ＭＯＮ， ∴∠ＭＱＮ＝∠ＭＢＮ． ∴∠ＭＣＰ＝∠ＭＢＮ． １０分!!!!!!!!!!!! ∵ＡＢ是⊙Ｏ的直径， ∴∠ＡＮＢ＝９０°． ∴在△ＡＮＢ中，∠ＮＢＡ＋∠ＮＡＢ＝９０°． ∴∠ＭＢＮ＋∠ＭＢＡ＋∠ＮＡＢ＝９０°． 即∠ＭＣＰ＋∠ＭＢＡ＋∠ＮＡＢ＝９０°． ２５．解：（１）把（１，－１）代入 ｙ＝ｘ２ ＋ｂｘ＋ｃ中，可得 ｂ＋ｃ＝ －２， １分!!!!!!!!!!!!!!!!!!! 又∵ｂ－ｃ＝４，可解得 ｂ＝１，ｃ＝－３； ３分!!!!!! （２）由 ｂ＋ｃ＝－２，得 ｃ＝－２－ｂ． 对于 ｙ＝ｘ２ ＋ｂｘ＋ｃ， 当 ｘ＝０时，ｙ＝ｃ＝－２－ｂ． ∵抛物线的对称轴为直线 ｘ＝－ｂ ２， ∴Ｂ（０，－２－ｂ），Ｃ（－ｂ ２，０）． ∵ｂ＞０， ∴ＯＣ＝ｂ ２，ＯＢ＝２＋ｂ． ５分!!!!!!!!!!! 当 ｋ＝３ ４时，由 ＯＣ＝３ ４ＯＢ得 ｂ ２ ＝３ ４（２＋ｂ），此时 ｂ＝ －６＜０不合题意． ∴对于任意的 ０＜ｋ＜１，不一定存在 ｂ，使得 ＯＣ＝ｋ·ＯＢ． ７分!!!!!!!!!!!!!!!!!!!!! （３）由平移前的抛物线 ｙ＝ｘ２ ＋ｂｘ＋ｃ，可得 ｙ＝（ｘ＋ｂ ２）２ －ｂ２ ４ ＋ｃ，即 ｙ＝（ｘ＋ｂ ２）２ －ｂ２ ４ －２－ｂ． ∵平移后 Ａ（１，－１）的对应点为 Ａ１（１－ｍ，２ｂ－１）； 可知，抛物线向左平移 ｍ个单位长度，向上平移 ２ｂ个单 位长度． 则平移后的抛物线解析式为 ｙ＝（ｘ＋ ｂ ２ ＋ｍ）２ －ｂ２ ４ －２ －ｂ＋２ｂ． ９分!!!!!!!!!!!!!!!!! 即 ｙ＝（ｘ＋ｂ ２ ＋ｍ）２ －ｂ２ ４ －２＋ｂ． 把（１，－１）代入，得（１＋ｂ ２ ＋ｍ）２ －ｂ２ ４ －２＋ｂ＝－１． （１＋ｂ ２ ＋ｍ）２ ＝ｂ２ ４ －ｂ＋１，即（１＋ ｂ ２ ＋ｍ）２ ＝（ｂ ２ － １）２． ∴１＋ｂ ２ ＋ｍ＝±（ｂ ２ －１）． 当 １＋ｂ ２ ＋ｍ＝ｂ ２ －１时，ｍ＝－２（不合题意，舍去）； 当 １＋ｂ ２ ＋ｍ＝－（ｂ ２ －１）时，ｍ＝－ｂ． １０分!!!! ∵ｍ≥ －３ ２，∴ｂ≤ ３ ２． ∴０＜ｂ≤ ３ ２． １１分!!!!!!!!!!!!!!! ∴平移后的抛物线解析式为 ｙ＝（ｘ－ｂ ２）２ －ｂ２ ４ －２＋ｂ． 即顶点为（ｂ ２，－ｂ２ ４ －２＋ｂ）． １２分!!!!!!!! 设 ｐ＝－ｂ２ ４ －２＋ｂ，即 ｐ＝－１ ４ （ｂ－２）２ －１． ∵ －１ ４ ＜０，∴当 ｂ＜２时，ｐ随 ｂ的增大而增大． ∵０＜ｂ≤ ３ ２， ∴当 ｂ＝３ ２时，ｐ取最大值，最大值为 －１７ １６． １３分!!! 此时，平移后抛物线的顶点所能达到的最高点坐标为 （３ ４，－１７ １６）． １４分                                                          !!!!!!!!!!!!!!! ６　　　　 ２０１７－２０１８学年福建省泉州市九年级（上）期末 数学试卷参考答案 一、选择题：本题共 １０小题，每小题 ４分，共 ４０分． １．Ｂ　２．Ａ　３．Ｂ　４．Ｄ　５．Ａ　６．Ｃ　７．Ｃ　８．Ｄ　９．Ｄ １０．Ａ 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分． １１．（－３，２）　１２．２　１３．３０°　１４．１ ３　１５．５７．５ １６．２０１６或 －２ 三、解答题：本题共 ９小题，共 ８６分． １７．解：原式 槡 槡 槡＝ ６－２ ６＋ ６＝０． １８．解：（１）将 ｘ＝４代入原方程，得：４２ －４×４＋（１－ｍ）＝０， 解得：ｍ＝１； （２）∵方程 ｘ２ －４ｘ＋（１－ｍ）＝０有两个不相等的实数 根， ∴Δ＝（－４）２ －４×１×（１－ｍ）＝１２＋４ｍ＞０， 解得：ｍ＞－３． １９．解：（１）如解图，△ＡＢ１Ｃ１即为所求； （２）Ｂ１（２，１），Ｃ１（０，７）． 第 １９题解图 ２０．解：由已知可得，∠ＡＣＢ＝４３°， ∵∠ＡＢＣ＝９０°，ＢＣ＝３０米， ∴ｔａｎ∠ＡＣＢ＝ＡＢ ＢＣ， ∴ＡＢ＝ｔａｎ４３°×３０≈０．９３２５×３０≈２８．０（米）， 答：Ａ处到地面 Ｂ处的距离 ＡＢ约为 ２８．０米． ２１．解：设宽为 ｘ米，则长为（ｘ＋１０）米， 依题意得：ｘ（ｘ＋１０）＝３７５， 解得：ｘ１ ＝１５，ｘ２ ＝－２５（舍去）． １０＋１５＝２５（米）． 答：绿地的长是 ２５米，宽是 １５米． ２２．解：（１）０．６； （２）根 据 表 格 中 数 据 知，摸 到 黑 棋 子 的 频 率 为 ２＋５＋１＋５＋４＋７＋４＋３＋３＋６ １００ ＝０．４， 设白棋子有 ｘ枚， 由题意，得： １０ １０＋ｘ＝０．４， 解得：ｘ＝１５， 经检验：ｘ＝１５是原分式方程的解，且符合实际意义． 答：白棋子的数量约为 １５枚． ２３．解：（１）Δ＝ｂ２ －４ａｃ； （２）∵ａ≠０，方程两边都除以 ａ，得：ｘ２ ＋ｂ ａｘ＋ ｃ ａ＝０， 移项，得：ｘ２ ＋ｂ ａｘ＝－ ｃ ａ， 配方，得：ｘ２ ＋２·ｘ· ｂ ２ａ＋（ｂ ２ａ）２ ＝（ｂ ２ａ）２ － ｃ ａ， 即：（ｘ＋ｂ ２ａ）２ ＝ｂ２ －４ａｃ ４ａ２ ， ∵ａ≠０， ∴４ａ２ ＞０． 当 ｂ２ －４ａｃ≥ ０ 时，直 接 开 平 方，得：ｘ＋ ｂ ２ａ ＝ ± ｂ２ －４槡 ａｃ ２ａ ， ∴ｘ＝－ｂ ２ａ± ｂ２ －４槡 ａｃ ２ａ ， 即：ｘ１ ＝－ｂ＋ ｂ２ －４槡 ａｃ ２ａ ，ｘ２ ＝－ｂ－ ｂ２ －４槡 ａｃ ２ａ ． 当 ｂ２ －４ａｃ＜０时，方程无实数根． ∴ｘ＝－ｂ± ｂ２ －４槡 ａｃ ２ａ （ｂ２ －４ａｃ≥０）． ２４．（１）证明：∵点 Ｄ关于 ＰＣ的对称点为 Ｅ， ∴ＰＣ⊥ＤＥ，ＥＭ＝ＤＭ． ∵ＥＦ⊥ＤＥ， ∴ＰＭ∥ＥＦ． ∴ＰＤ ＰＦ＝ＤＭ ＥＭ＝１． ∴ＰＤ＝ＰＦ； （２）解：∵∠ＥＡＦ＝∠ＤＥＦ＝∠ＰＭＤ＝９０°， ∴∠ＡＥＦ＋∠ＡＦＥ＝∠ＡＥＦ＋∠ＡＥＤ＝∠ＤＰＭ＋ＰＤＭ＝ ∠ＤＰＭ＋∠ＰＣＤ＝９０°， ∴∠ＦＥＡ＝∠ＥＤＡ＝∠ＰＣＤ， ∴ｔａｎ∠ＦＥＡ＝ｔａｎ∠ＥＤＡ＝ｔａｎ∠ＰＣＤ， ∴ＡＦ ＡＥ＝ＡＥ ＡＤ＝ＰＤ ＣＤ， ∵ＤＰ∶ＰＡ＝２∶１， ∴设 ＰＡ＝ｘ，ＰＤ＝２ｘ，ＡＥ＝ｙ， ①当点 Ｐ在线段 ＤＡ上，如解图①，ＡＤ＝３ｘ， 第 ２４题解图① ∵ＰＦ＝ＰＤ＝２ｘ，ＰＡ＝ｘ， ∴ＡＦ＝ｘ， ∴ ｘ ｙ＝２ｘ ４， 解得：ｙ＝２， ②当点 Ｐ在 ＤＡ的延长线上时，如解图②， 第 ２４题解图②                                                                   ７　　　　 ∵ＰＦ＝ＰＤ＝２ｘ，ＰＡ＝ｘ， ∴ＡＦ＝３ｘ，ＡＤ＝ｘ， ∴３ｘ ｙ＝２ｘ ４， 解得：ｙ＝６， 综上所述，ＡＥ＝２或 ６． ２５．解：（１）∵Ａ（－２，０）在 ｙ＝ｋｘ 槡－２ ３的图象上， ∴ －２ｋ 槡－２ ３＝０， ∴ｋ 槡＝－ ３； （２）∵∠ＰＯＡ＝∠ＡＯＢ＝９０°，Ｐ（０，ｍ）， ∴ＯＰ＝｜ｍ｜， 由（１）得 ｙ 槡＝－ ３ｘ 槡－２ ３， 将 ｘ＝０代入 ｙ 槡＝－ ３ｘ 槡－２ ３中， 令 ｘ＝０， 得 ｙ 槡＝－２ ３， ∴ＯＢ 槡＝２ ３， ∵Ａ（－２，０）， ∴ＯＡ＝２， ∵△ＰＯＡ∽△ＡＯＢ， ∴ＯＰ ＯＡ＝ＯＡ ＯＢ， ∴ ｜ｍ｜ ２ ＝ ２ 槡２ ３ ， ∴ｍ＝± 槡２ ３ ３ ； （３）如解图，取点 Ｅ（ 槡２ ３，０），连接 ＢＥ，过点 Ａ作 ＡＤ⊥ＢＥ 于 Ｄ，过点 Ｐ作 ＰＣ⊥ＢＥ于 Ｃ， 在 Ｒｔ△ＢＯＥ中，ＯＢ＝ＯＥ 槡＝２ ３， ∴∠ＯＢＥ＝４５°，ＢＥ 槡＝ ２ＯＢ 槡＝２ ６， 在 Ｒｔ△ＰＣＢ中，∠ＰＣＢ＝９０°， ∴ＰＣ＝ＢＰ·ｓｉｎ∠ＰＢＣ＝ＢＰ·ｓｉｎ４５°＝槡２ ２ＢＰ， 槡∴ ２ＰＡ＋ＰＢ 槡＝ ２（ＰＡ＋槡２ ２ＰＢ） 槡＝ ２（ＰＡ＋ＰＣ）≥槡２ＡＤ， 当且仅当 Ａ，Ｐ，Ｃ三点共线时，取等号，此时，点 Ｃ，Ｄ重 合， ∵Ｓ△ＡＢＥ ＝１ ２ＡＥ·ＯＢ＝１ ２ＢＥ·ＡＤ， ∴ＡＤ＝ＡＥ·ＯＢ ＢＥ ＝ 槡２ ３（ 槡２ ３＋２） 槡２ ６ 槡 槡＝ ２＋ ６， ∴（槡２ＰＡ＋ＰＢ）ｍｉｎ 槡＝ ２（槡 槡２＋ ６） 槡＝２＋２ ３． 第 ２５题解图                                  ８　　　　 ２０１７－２０１８学年福建省漳州市九年级（上）期末数学试卷 参考答案 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分．） １．Ａ　２．Ｃ　３．Ａ　４．Ｃ　５．Ｄ　６．Ｂ　７．Ｂ　８．Ｄ　９．Ａ １０．Ｄ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．＞　１２．－２　１３．１ ２ １４．∠ＡＤＥ＝∠Ｃ或∠ＡＥＤ＝∠Ｂ或ＢＤ ＡＣ＝ＡＥ ＡＢ（答案不唯一） １５．１３２０（１－ｘ）２ ＝６６０　１６． 槡１２ ３ 三、解答题（本大题共 ９小题，满分 ８６分．） １７．解：（１）原式 槡 槡 槡＝３ ３＋ ３－２ ３ 槡＝２ ３； （２）原式 ＝３－４ ＝－１． １８．解：（１）ｘ（２ｘ－５）＝０， ∵ｘ＝０或 ２ｘ－５＝０， ∴ｘ１ ＝０，ｘ２ ＝５ ２； （２）ｘ２ 槡－２ ３ｘ＋３＝０， （ｘ 槡－ ３）２ ＝０， ∴ｘ１ ＝ｘ２ 槡＝ ３． １９．解：由题意可得 Δ＝（－ｍ）２ －４（ｍ－２）＝ｍ２ －４ｍ＋８＝ （ｍ－２）２ ＋４， ∵（ｍ－２）２≥０， ∴（ｍ－２）２ ＋４＞０，即 Δ＞０， ∴对于任何实数 ｍ，此方程总有两个不相等的实数根． ２０．（１）解：作 ＡＤ如解图所示： 第 ２０题解图 　　 （２）证明：∵∠ＢＡＣ＝９０°，ＡＤ⊥ＢＣ， ∴∠ＡＤＢ＝∠ＡＤＣ＝９０°， ∵∠２＋∠１＝９０°，∠１＋∠Ｃ＝９０°， ∴∠２＝∠Ｃ， ∴△ＡＤＢ∽△ＣＤＡ， ∴ＡＤ ＣＤ＝ＤＢ ＤＡ， ∴ＡＤ２ ＝ＢＤ·ＣＤ． ２１．解：如解图，过点 Ａ作 ＡＭ⊥ＢＦ于点 Ｍ， 第 ２１题解图 在 Ｒｔ△ＡＭＢ中，ｓｉｎ７５°＝ＡＭ ＡＢ， ∴ＡＭ＝ＡＢ·ｓｉｎ７５°≈９０×０．９６６＝８６．９４ｃｍ， ∴ＡＭ＋ＥＨ＝８６．９４＋４≈９０．９ｃｍ． 答：点 Ａ到地面的距离约为 ９０．９ｃｍ． ２２．解：画树状图如解图： 第 ２２题解图 由树状图可知，共有 １２种等可能的结果，其中乘积 ａ≥ １０的结果有 ２种，４＜ａ＜１０的结果有 ４种，ａ≤４的有 ６种， ∴获得一等奖的概率为 ２ １２＝１ ６， 获得二等奖的概率为 ４ １２＝１ ３， 获得三等奖的概率为 ６ １２＝１ ２， ∵ １ ２ ＞１ ３ ＞１ ６， ∴获得三等奖的概率最大． ２３．解：设其中一个正方形的边长为 ｘｃｍ，则另一个正方形 的边长为（１４－ｘ）ｃｍ， 根据题意得：ｘ２ ＋（１４－ｘ）２ ＝１００， 解得：ｘ１ ＝６，ｘ２ ＝８， 当 ｘ＝６时，１４－ｘ＝８； 当 ｘ＝８时，１４－ｘ＝６． 答：这两个正方形的边长分别为 ６ｃｍ、８ｃｍ． ２４．解：（１）槡２； （２）如解图，∵ＡＢ＝ＡＣ，ＤＥ＝ＢＤ， ∴△ＡＢＣ和△ＢＤＥ都是等腰三角形，且∠ＢＤＥ＝∠ＢＡＣ ＝１２０°， ∴∠１＝∠２＝∠３＝∠４＝３０°， ∴△ＡＢＣ∽△ＤＢＥ， ∴ＡＢ ＤＢ＝ＢＣ ＢＥ， ∴ＡＢ ＢＣ＝ＤＢ ＢＥ， ∵∠１＋∠ＣＢＤ＝∠３＋∠ＣＢＤ， ∴∠ＡＢＤ＝∠ＣＢＥ， ∴△ＣＢＥ∽△ＡＢＤ， ∴ＣＥ ＡＤ＝ＢＥ ＢＤ， 过点 Ｄ作 ＤＭ⊥ＢＥ于 Ｍ， ∴∠ＢＤＭ＝１ ２∠ＢＤＥ＝６０°，ＢＥ＝２ＢＭ， 在 Ｒｔ△ＢＤＭ中，ｓｉｎ∠ＢＤＭ＝ＢＭ ＢＤ， ∴ｓｉｎ６０°＝ＢＭ ＢＤ＝槡３ ２， ∴ＣＥ ＡＤ＝２ＢＭ ＢＤ 槡＝ ３； 第 ２４题解图                                                                   ９　　　　 （３）２ｓｉｎα ２． ２５．解：（１）３； 【解法提示】∵Ａ（３，０），Ｃ（－１，０）， ∴ＡＣ＝４， 在 Ｒｔ△ＡＢＣ中，ＡＢ＝５，根据勾股定理得，ＢＣ＝３． （２）当且仅当∠ＡＢＤ＝∠ＡＣＢ＝９０°时，△ＡＤＢ与△ＡＢＣ 相似，如解图①，过点 Ｂ作 ＤＢ⊥ＡＢ交 ｘ轴于点 Ｄ， ∴ＡＤ ＡＢ＝ＡＢ ＡＣ， ∵ＡＣ＝４，ＡＢ＝５， ∴ＡＤ ５ ＝５ ４， ∴ＡＤ＝２５ ４． ∴ＣＤ＝２５ ４ －４＝９ ４， ∴ＯＤ＝９ ４ ＋１＝１３ ４， ∴点 Ｄ的坐标为（－１３ ４，０）； 第 ２５题解图① （３）存在， ∵∠ＰＡＱ＝∠ＢＡＤ，要使△ＡＰＱ与△ＡＤＢ相似，分两种情 况： ①如解图②，当△ＡＰＱ∽△ＡＤＢ时，∴ＡＰ ＡＤ＝ＡＱ ＡＢ， ∵ＡＰ＝ｋ， ∴ＡＱ＝５－ｋ， ∴ ｋ ２５ ４ ＝５－ｋ ５ ， 解得 ｋ＝２５ ９； 第 ２５题解图② ②如解图③，当△ＡＰＱ∽△ＡＢＤ时， ∴ＡＰ ＡＢ＝ＡＱ ＡＤ， ∴ ｋ ５ ＝５－ｋ ２５ ４ ， 解得 ｋ＝２０ ９， 综上所述，ｋ＝２５ ９或２０ ９时，△ＡＰＱ与△ＡＤＢ相似． 第 ２５题解图③                                       １０　　　 ２０１７－２０１８学年福建省宁德市九年级（上）期末数学试卷 参考答案 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分．） １．Ｂ　２．Ｃ　３．Ａ　４．Ｄ　５．Ｂ　６．Ａ　７．Ａ　８．Ｄ　９．Ｄ １０．Ｃ 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分．） １１．槡３　１２．中心投影　１３．１２　１４．ｙ＝２ｘ２ ＋３　１５．２０　 １６．１ ４ 三、解答题（本大题有 ９小题，共 ８６分．） １７．解：∵ＤＥ∥ＢＣ， ∴ＡＤ ＡＢ＝ＡＥ ＡＣ，即 ５ １３＝３ ＡＣ， 解得 ＡＣ＝９． 即 ＡＣ的长为 ９． １８．解：当 ｘ＝３时，原方程为 ３２ －４×３＋ｃ＝０， 解得：ｃ＝３． ∴一元二次方程为 ｘ２ －４ｘ＋３＝０， （ｘ－１）（ｘ－３）＝０， ∴ｘ１ ＝１，ｘ２ ＝３． ∴ｃ的值为 ３，方程的另一个根为 １． １９．解：画树状图如解图： 第 １９题解图 由树状图可知共有 １２种等可能的结果，其中这两张联纸 恰好组成一副对联的结果有 ４种， ∴这两张联纸恰好组成一副对联的概率为 ４ １２＝１ ３． ２０．解：（１）∵点 Ａ（５，２）在反比例函数 ｙ＝ｋ ｘ的图象上， ∴ｋ＝１０， ∴反比例函数的解析式为 ｙ＝１０ ｘ； （２）由题意：１ ２ ×５×（ｎ－２）＝１０， ∴ｎ＝６， ∴Ｂ（５ ３，６）． ２１．（１）解：如解图，点 Ｅ，Ｆ即为所作； 第 ２１题解图 （２）证明：∵四边形 ＡＢＣＤ为平行四边形， ∴ＡＤ∥ＢＣ， ∴∠ＡＦＥ＝∠ＣＥＦ， ∵ＥＦ垂直平分 ＡＣ， ∴ＦＡ＝ＦＣ，ＥＦ⊥ＡＣ， ∴∠ＣＦＥ＝∠ＡＦＥ， ∴∠ＣＦＥ＝∠ＣＥＦ， ∴ＣＥ＝ＣＦ， ∴四边形 ＡＥＣＦ是菱形． ２２．解：如解图，在线段 ＣＤ上取点 Ｅ，过点 Ｅ作 ＥＦ⊥ＡＢ于点 Ｆ，作 ＥＧ⊥ＢＣ于点 Ｇ，过点 Ｄ作 ＤＨ⊥ＥＦ于点 Ｆ，则四边 形 ＤＨＦＡ和四边形 ＥＦＢＧ是矩形． 设 ＢＦ＝１．１ｍ，则 ＡＦ＝２－１．１＝０．９ｍ， 故 ＤＨ＝０．９ｍ， 则 ｔａｎ３１°＝ＥＨ ＤＨ＝ＥＨ ０．９≈０．６， 故 ＥＨ≈０．５４ｍ， 则 ＥＦ＝０．８＋０．５４＝１．３４ｍ＞１．１ｍ． 故该包裹能平放入这个储藏室． 第 ２２题解图 ２３．解：（１）２０－ｘ，４０＋５ｘ； （２）根据题意，得：（２０－ｘ）（４０＋５ｘ）＝９００， 整理，得：ｘ２ －１２ｘ＋２０＝０， 解得：ｘ＝２或 ｘ＝１０， 答：每件 Ｔ恤应降价 ２元或 １０元； （３）∵Ｓ＝（２０－ｘ）（４０＋５ｘ） ＝－５ｘ２ ＋６０ｘ＋８００ ＝－５（ｘ－６）２ ＋９８０， ∴顶点 Ａ的坐标为（６，９８０），其表示的实际意义为当降 价 ６元时，日盈利额取得最大值，最大利润为 ９８０元． ２４．（１）证明：∵四边形 ＡＢＣＤ为正方形， ∴∠ＡＢＥ＝∠ＡＤＣ＝∠ＡＤＦ＝９０°，ＡＢ＝ＡＤ， 在△ＡＢＥ和△ＡＤＦ中， ＢＥ＝ＤＦ ∠ＡＢＥ＝∠ＡＤＦ ＡＢ＝{ ＡＤ ， ∴△ＡＢＥ≌△ＡＤＦ（ＳＡＳ）， ∴ＡＥ＝ＡＦ； （２）解：ＡＭ⊥ＥＦ，ＡＭ＝１ ２ＥＦ，理由如下： 由（１）得：△ＡＢＥ≌△ＡＤＦ， ∴∠ＥＡＢ＝∠ＦＡＤ， ∴∠ＦＡＥ＝∠ＤＡＢ＝９０°， ∴△ＦＡＥ是等腰直角三角形， 如解图，过 Ｅ作 ＥＮ∥ＣＤ，交 ＢＤ于点 Ｎ， ∴∠ＭＮＥ＝∠ＭＤＦ，∠ＭＥＮ＝∠ＭＦＤ， ∵四边形 ＡＢＣＤ为正方形， ∴∠ＮＢＥ＝４５°， ∴△ＮＢＥ是等腰直角三角形， ∴ＥＮ＝ＢＥ＝ＤＦ， 在△ＭＮＥ和△ＭＤＦ中， ∵ ∠ＭＮＥ＝∠ＭＤＦ ＮＥ＝ＤＦ ∠ＭＥＮ＝∠{ ＭＦＤ                                                                   ， １１　　　 ∴△ＭＮＥ≌△ＭＤＦ（ＡＳＡ）， ∴ＥＭ＝ＦＭ， ∴ＡＭ⊥ＥＦ，ＡＭ＝１ ２ＥＦ． 第 ２４题解图 ２５．解：（１）∵ｂ＝６，ｃ＝－５， ∴二次函数的解析式为 ｙ＝－ｘ２ ＋６ｘ－５， 令 ｙ＝０， 则 －ｘ２ ＋６ｘ－５＝０， ∴ｘ＝１或 ｘ＝５， ∴Ａ（１，０），Ｂ（５，０）； （２）∵点 Ａ的坐标为（１，０）， ∴０＝－１＋ｂ＋ｃ， ∴ｃ＝－ｂ＋１， ∴二次函数的解析式为 ｙ＝－ｘ２ ＋ｂｘ－ｂ＋１＝－（ｘ－１） （ｘ－ｂ＋１）， ∴抛物线的对称轴为直线 ｘ＝ｂ ２， 令 ｙ＝０， ∴０＝－ｘ２ ＋ｂｘ－ｂ＋１， ∴ｘ＝１或 ｘ＝ｂ－１， ∴Ｂ（ｂ－１，０）， ∵点 Ａ在点 Ｂ的左边， ∴ｂ－１＞１， ∴ｂ＞２， ∴ＡＢ＝ｂ－１－１＝ｂ－２， ∵ＰＥ⊥ｙ轴， ∴ＰＥ∥ＡＢ， ∵四边形 ＡＢＰＥ是平行四边形， ∴ＰＥ＝ＡＢ， ∴ｂ－２＝ｂ ２， ∴ｂ＝４， ∴ｃ＝－ｂ＋１＝－３； （３）∵ｂ＝７， ∴二次函数的解析式为 ｙ＝－ｘ２ ＋７ｘ＋ｃ， 令 ｙ＝０， ∴０＝－ｘ２ ＋７ｘ＋ｃ， ∴ Δ＝４９＋４ｃ＞０， ∴ｃ＞－４９ ４， ∵点 Ａ，Ｂ在点（１，０）与点（５，０）之间， ∴ －１＋７＋ｃ＜０且 －２５＋３５＋ｃ＜０， 解得 ｃ＜－６且 ｃ＜－１０， ∴ｃ＜－１０， ∴ －４９ ４ ＜ｃ＜－１０                                   ． １２　　　 ２０１７－２０１８学年福建省龙岩市上杭县九年级（上）期末数学试卷 参考答案 一、选择题：本题共 １０小题，每小题 ４分，共 ４０分，在每小题 给出的四个选项中，只有一项是符合题目要求的． １．Ａ　２．Ｂ　３．Ａ　４．Ｄ　５．Ｃ　６．Ｂ　７．Ｃ　８．Ｂ　９．Ａ １０．Ａ 二、填空题：本题共 ６小题，每小题 ４分，共 ２４分． １１．２　１２．７０°　１３．６　１４．－５　１５．（１，－１）　１６．６ 三、解答题：本题共 ９个小题，共 ８６分．解答应写出文字说明、 证明过程或演算步骤． １７．（１）解：原方程可变形为 ｘ２ ＝４． ∴ｘ１ ＝２，ｘ２ ＝－２； （２）解：移项得 ２ｘ２ －４ｘ＝７． 二次项系数化为 １，得 ｘ２ －２ｘ＝７ ２； 配方得 ｘ２ －２ｘ＋１＝７ ２ ＋１， 即（ｘ－１）２ ＝９ ２， 开方得：ｘ－１＝± 槡３ ２ ２ ， ∴ｘ１ ＝ 槡２＋３ ２ ２ ，ｘ２ ＝ 槡２－３ ２ ２ ． １８．解：（１）令 ｙ＝０，则 ｘ２ －４ｘ＋３＝０， 解得 ｘ１ ＝１，ｘ２ ＝３， ∴图象与 ｘ轴的交点坐标为（１，０）（３，０）， 令 ｘ＝０，则 ｙ＝３， ∴与 ｙ轴的交点坐标为（０，３）， ∵ｙ＝ｘ２ －４ｘ＋３＝（ｘ－２）２ －１， ∴顶点坐标为（２，－１）， 函数图象如解图所示； 第 １８题解图 （２）由解图可知，ｘ＜１或 ｘ＞３时，ｙ＞０． １９．解：（１）如解图①，点 Ｏ为所求； 第 １９题解图① （２）如解图②，连接 ＯＡ，ＯＣ，ＯＣ交 ＡＢ于 Ｄ， 第 １９题解图② ∵Ｃ为 ) ＡＢ的中点， ∴ＯＣ⊥ＡＢ， ∴ＡＤ＝ＢＤ＝１ ２ＡＢ＝４０， 设⊙Ｏ的半径为 ｒ，则 ＯＡ＝ｒ，ＯＤ＝ＯＣ－ＣＤ＝ｒ－２０， 在 Ｒｔ△ＯＡＤ中，∵ＯＡ２ ＝ＯＤ２ ＋ＡＤ２， ∴ｒ２ ＝（ｒ－２０）２ ＋４０２，解得 ｒ＝５０， 即 ) ＡＢ所在圆的半径是 ５０ｍ． ２０．解：（１）∵ＣＢ＝ＣＡ，∠ＡＣＢ＝９０°， ∴∠ＣＡＢ＝４５°． 依题意知，△ＢＣＤ≌△ＡＣＥ， ∴ＡＥ＝ＢＤ，∠ＣＡＥ＝∠Ｂ＝４５°， ∵∠ＤＡＥ＝∠ＢＡＣ＋∠ＣＡＥ， ∴∠ＤＡＥ＝９０°； （２）∵ＡＢ＝４，ＢＤ∶ＤＡ＝１∶３， ∴ＢＤ＝１ ４ＡＢ＝１，ＤＡ＝３，ＢＤ＝ＡＥ＝１， 在 Ｒｔ△ＡＤＥ中，∵ＤＥ２ ＝１２ ＋３２ ＝１０， ∴ＤＥ 槡＝ １０． ２１．解：（１）∵ＣＤ∥ｙ轴， ∴Ｃ和 Ｄ的横坐标相等， ∵Ａ（ｍ，２ ３）， ∴点 Ｄ的横坐标为：ｍ－２； （２）∵ＣＤ＝２， ∴点 Ｄ的坐标为（ｍ－２，２）， ∵点 Ａ（ｍ，２ ３）、Ｄ（ｍ－２，２）均在反比例函数 ｙ＝ ｋ ｘ（ｘ＞ ０）图象上， ∴ ２ ３ｍ＝２（ｍ－２）． 解得 ｍ＝３． ∴反比例函数的解析式为：ｙ＝２ ｘ（ｘ＞０）． ２２．解：（１）∵确定小英打第 １场， ∴只要再从小丽、小敏、小洁三人中选 １人， ∴Ｐ（恰好选中小洁）＝１ ３； （２）画树状图如解图： 第 ２２题解图 由树状图可知，共有 ８种等可能的结果，其中小丽和小敏 打第一场的结果共有 ２种，从而所求概率 Ｐ＝２ ８ ＝１ ４． ２３．解：（１）Ｓ＝ｘ（４０－２ｘ）＝－２ｘ２ ＋４０ｘ； （２）由题意，得：０＜４０－２ｘ≤２４， 解得 ８≤ｘ＜２０， 又由（１）得 Ｓ＝－２（ｘ－１０）２ ＋２００                                                                   ， １３　　　 ∴当 ｘ＝１０时，所围成的花圃面积最大，最大值为 ２００ ｍ２； （３）由 －２（ｘ－１０）２ ＋２００＝１５０， 解得 ｘ１ ＝５，ｘ２ ＝１５， ∵８≤ｘ＜２０， ∴当花圃的面积为 １５０ｍ２时，ＡＢ长为 １５米． ２４．（１）证明：∵四边形 ＡＢＣＤ的对角线交于点 Ｅ，且 ＡＥ＝ ＥＣ，ＢＥ＝ＥＤ， ∴四边形 ＡＢＣＤ是平行四边形， ∵以 ＡＤ为直径的半圆过点 Ｅ， ∴∠ＡＥＤ＝９０°，即有 ＡＣ⊥ＢＤ， ∴四边形 ＡＢＣＤ是菱形； （２）解：由（１）知，四边形 ＡＢＣＤ是菱形， ∴△ＡＤＣ为等腰三角形． ∴ＡＤ＝ＤＣ且 ＤＥ⊥ＡＣ，∠ＡＤＥ＝∠ＣＤＥ． 如解图，过点 Ｃ作 ＣＧ⊥ＡＤ，垂足为 Ｇ，连接 ＦＯ， 第 ２４题解图 ∵ＢＦ切⊙Ｏ于点 Ｆ， ∴ＯＦ⊥ＡＤ，且 ＯＦ＝１ ２ＡＤ＝３， 易知，四边形 ＣＧＯＦ为矩形， ∴ＣＧ＝ＯＦ＝３． 在 Ｒｔ△ＣＤＧ中，ＣＤ＝ＡＤ＝６，ｓｉｎ∠ＡＤＣ＝ＣＧ ＣＤ＝１ ２， ∴∠ＣＤＡ＝３０°． ∴∠ＡＤＥ＝１５°． 连接 ＯＥ，则∠ＡＯＥ＝２×∠ＡＤＥ＝３０°， ∴ ) ＡＥ＝３０·π×３ １８０ ＝π ２． ２５．解：（１）∵Ａ（－１，０），Ｂ（２，－３）在 ｙ＝ｘ２ ＋ｂｘ＋ｃ上， ∴ １－ｂ＋ｃ＝０， ４＋２ｂ＋ｃ＝－３{ ， 解得 ｂ＝－２， ｃ＝－３{ ， ∴抛物线的解析式为：ｙ＝ｘ２ －２ｘ－３． ∵ｙ＝ｘ２ －２ｘ－３＝（ｘ－１）２ －４， ∴抛物线的顶点坐标为（１，－４）； （２）∵Ｐ（ｓ，ｔ）关于原点的对称点为 Ｐ′（－ｓ，－ｔ）， ∴ ｓ２ －２ｓ－３＝ｔ （－ｓ）２ －２（－ｓ）－３＝－{ ｔ ， 即 ｓ２ －２ｓ－３＝ｔ① ｓ２ ＋２ｘ－３＝－ｔ{ ② ， ① ＋②，解得 ｓ１ 槡＝ ３，ｓ２ 槡＝－ ３； （３）依题意，∵抛物线过 Ｍ（ｍ，ｎ），Ｑ（ｍ＋８，ｎ）点， 代入抛物线 ｙ＝ｘ２ ＋ｂｘ＋ｃ得， ｍ２ ＋ｂｍ＋ｃ＝ｎ， （ｍ＋８）２ ＋ｂ（ｍ＋８）＋ｃ＝ｎ{ ， 解得 ｂ＝－８－２ｍ， ∴ｙ＝ｘ２ ＋ｂｘ＋ｃ＝ｘ２ －（８＋２ｍ）ｘ＋ｃ． ∴抛物线的对称轴为：ｘ＝ｍ＋４， 设抛物线的解析式为 ｙ＝（ｘ－ｍ－４）２ ＋ｋ， ∵抛物线过点 Ｍ，Ｎ， ∴ １６＋ｋ＝ｎ， ４＋ｋ＝１ ７ｎ{ ， 解得 ｎ＝１４， ｋ＝－２{ ． ∴Ｓ△ＭＮＱ ＝１ ２ＭＱ·（ｎ－１ ７ｎ）＝１ ２ ×８×６ ７ ×１４＝４８                                         ． １４　　　 ２０１７－２０１８南平市学年九年级（上）期末质量检测 数学试题参考答案 一、选择题（本大题共 １０小题，每小题 ４分，共 ４０分） １．Ｄ　２．Ａ　３．Ｂ　４．Ｃ　５．Ｃ　６．Ｂ　７．Ｃ　８．Ｂ　９．Ｄ １０．Ｄ． 二、填空题（本大题共 ６小题，每小题 ４分，共 ２４分） １１．ｙ＝１ ｘ（答案不唯一，０＜ｋ＜２的任何一个数） １２．２　１３．１８０　１４．１１４　１５．２．５　１６．０＜ａ＜３ 三、解答题（本大题共 ９小题，共 ８６分） １７．解：（１）ｘ（ｘ＋２）＝０， ２分!!!!!!!!!!!! ∴ｘ１ ＝０，ｘ２ ＝－２． ４分!!!!!!!!!!!!!! （２）∵ａ＝３，ｂ＝２，ｃ＝－１， ∴Δ＝２２ －４×３×（－１）＝１６， ∴ｘ＝ 槡－２± １６ ２×３ ＝－２±４ ６ ， ２分!!!!!!!!!! ∴ｘ１ ＝１ ３，ｘ２ ＝－１． ４分!!!!!!!!!!!!! １８．（１）证明：∵ａ＝ｋ，ｂ＝ｋ＋３，ｃ＝３， ∴Δ＝（ｋ＋３）２ －４·ｋ·３＝ｋ２ －６ｋ＋９＝（ｋ－３）２≥０， ２分 ! !!!!!!!!!!!!!!!!!!!! ∴方程一定有两个实数根． ３分!!!!!!!!!! （２）解：由（１）得 Δ＝（ｋ＋３）２ －４·ｋ·３＝（ｋ－３）２， ∴ｘ＝－（ｋ＋３）± （ｋ－３）槡 ２ ２ｋ ＝－ｋ－３±（ｋ－３） ２ｋ ， ∴ｘ１ ＝－１，ｘ２ ＝－３ ｋ， ６分!!!!!!!!!!!! ∵方程的两个实数根都是整数， ∴正整数 ｋ＝１或 ３． ８分!!!!!!!!!!!!! １９．解：（１）方法一：列表： 　　ｙ ｘ　　 １ ２ ３ ０ （０，１） （０，２） （０，３） １ （１，１） （１，２） （１，３） ２ （２，１） （２，２） （２，３） 从表格中可知，点 Ｍ坐标总共有九种等可能的情况：（０， １），（０，２），（０，３），（１，１），（１，２），（１，３），（２，１），（２，２）， （２，３）； ３分!!!!!!!!!!!!!!!!!! 方法二：画树状图如解图， 第 １９题解图 从树状图中可知，点 Ｍ坐标总共有九种等可能的情况： （０，１），（０，２），（０，３），（１，１），（１，２），（１，３），（２，１），（２， ２），（２，３）； ３分!!!!!!!!!!!!!!!! （２）当 ｘ＝０时，ｙ＝－０＋３＝３， 当 ｘ＝１时，ｙ＝－１＋３＝２， 当 ｘ＝２时，ｙ＝－２＋３＝１， ６分!!!!!!!!!! 由（１）可得点 Ｍ坐标总共有九种等可能的情况，点 Ｍ落 在直线 ｙ＝－ｘ＋３上（记为事件 Ａ）有 ３种情况． ∴Ｐ（Ａ）＝３ ９ ＝１ ３． ８分!!!!!!!!!!!!! ２０．解：当 ｘ＝０时，ｙ＝２，∴Ａ（０，２）， ２分!!!!!!! ∴ＡＯ＝２，∵ＡＯ＝２ＢＯ，∴ＢＯ＝１， ４分!!!!!!! 当 ｘ＝１时，ｙ＝１＋２＝３，∴Ｃ（１，３）， ６分!!!!!! 把 Ｃ（１，３）代入 ｙ＝ｋ ｘ，解得：ｋ＝３． ∴反比例函数的解析式为：ｙ＝３ ｘ． ８分!!!!!!! ２１．解：（１）作△ＡＤ′Ｃ′如解图； ３分!!!!!!!!!! 第 ２１题解图 （２）∵将△ＡＤＣ绕点 Ａ顺时针方向旋转得到△ＡＤ′Ｃ′，点 Ｃ与点 Ｃ′为对应点， ∴△ＡＤＣ≌△ＡＤ′Ｃ′， ∴ＡＣ＝ＡＣ′，ＡＤ＝ＡＤ′＝５，ＣＤ＝ＣＤ′＝１０，∠ＡＤＣ＝∠ＡＤ′Ｃ′ ＝９０°，∠ＡＣＤ＝∠ＡＣ′Ｄ′， ∵ＡＢ∥ＣＤ，∴∠ＢＡＣ＝∠ＡＣＤ， ∵ＡＢ⊥ＣＣ′，ＡＣ＝ＡＣ′， ∴∠ＢＡＣ＝∠Ｃ′ＡＢ， ∴∠ＡＣ′Ｄ′＝∠Ｃ′ＡＢ，∴Ｃ′Ｅ＝ＡＥ． ５分!!!!!!! 在 Ｒｔ△Ｃ′ＢＥ中，Ｃ′Ｂ２ ＋ＢＥ２ ＝Ｃ′Ｅ２，设 ＡＥ＝ｘ，则 ＢＥ＝ＡＢ －ＡＥ＝１０－ｘ， ５２ ＋（１０－ｘ）２ ＝ｘ２， ７分!!!!!!!!!!!!! 解得：ｘ＝２５ ４． 答：ＡＥ的长为２５ ４． ８分!!!!!!!!!!!!!! ２２．解：（１）∵正方形 ＡＥＦＧ和正方形 ＪＫＣＩ全等，矩形 ＧＨＩＤ 和矩形 ＥＢＫＬ全等， 设 ＡＧ＝ｘ，则 ＤＧ＝６－ｘ，ＢＥ＝８－ｘ，ＦＬ＝ｘ－（６－ｘ）＝２ｘ －６，ＬＪ＝８－２ｘ， ∵Ｓ矩形ＬＪＨＦ ＝ＦＬ·ＬＪ， ∴（２ｘ－６）（８－２ｘ）＝３ ４， ２分!!!!!!!!!! ∴ｘ１ ＝１３ ４，ｘ２ ＝１５ ４， ∴ＡＧ＝１３ ４或 ＡＧ＝１５ ４； ４分!!!!!!!!!!!! （２）设矩形 ＬＪＨＦ的面积为 Ｓ， Ｓ＝（２ｘ－６）（８－２ｘ） ６分!!!!!!!!!!!! ＝－４ｘ２ ＋２８ｘ－４８ ＝－４（ｘ－７ ２）２ ＋１． ８分!!!!!!!!!!!! ∵ａ＝－４＜０                                                                   ， １５　　　 ∴Ｓ有最大值， ∴当 ＡＧ＝７ ２ 时，矩形 ＬＪＨＦ的面积最大． １０分!!! ２３．证明：方法一：如解图，连接 ＯＤ， ∵ＡＣ＝ＣＤ＝ＤＢ， ∴ ) ＡＣ＝ ) ＣＤ＝ ) ＤＢ， ∴∠ＡＯＣ＝∠ＣＯＤ＝∠ＢＯＤ， ２分!!!!!!!!! ∴∠ＣＯＢ＝∠ＣＯＤ＋∠ＤＯＢ＝２∠ＣＯＤ＝２∠ＡＯＣ， ∵∠ＣＯＢ＝２∠ＣＡＥ，∴∠ＡＯＣ＝∠ＣＡＥ， ４分!!!!! 在△ＡＯＣ中，ＯＡ＝ＯＣ， ∴∠ＡＣＯ＝１８０°－∠ＡＯＣ ２ ＝９０°－∠ＡＯＣ ２ ， ５分!!!! 在△ＡＣＥ中，∠ＡＥＣ＝１８０°－∠ＣＡＥ－∠ＡＣＥ ＝１８０°－∠ＡＯＣ－（９０°－∠ＡＯＣ ２ ） ＝９０°－∠ＡＯＣ ２ ， ６分!!!!!!!!!!!!!! ∴∠ＡＣＥ＝∠ＡＥＣ， ７分!!!!!!!!!!!!! ∴ＡＣ＝ＡＥ， ８分!!!!!!!!!!!!!!!! ∵ＡＣ＝ＣＤ，∴ＡＥ＝ＣＤ． １０分!!!!!!!!!!! 第 ２３题解图 方法二：如解图，连接 ＯＤ， ∵ＡＣ＝ＣＤ＝ＤＢ， ∴ ) ＡＣ＝ ) ＣＤ＝ ) ＤＢ， ∴∠ＡＯＣ＝∠ＣＯＤ＝∠ＢＯＤ， ２分!!!!!!!!! ∴∠ＣＯＢ＝∠ＣＯＤ＋∠ＤＯＢ＝２∠ＣＯＤ＝２∠ＡＯＣ， ∵∠ＣＯＢ＝２∠ＣＡＥ，∴∠ＡＯＣ＝∠ＣＡＥ， ４分!!!!! ∵∠ＣＡＯ＝∠ＣＡＥ＋∠ＥＡＯ，∠ＡＥＣ＝∠ＡＯＣ＋∠ＥＡＯ， ∴∠ＣＡＯ＝∠ＡＥＣ， ６分!!!!!!!!!!!!! 在△ＡＯＣ中，ＯＡ＝ＯＣ， ∴∠ＡＣＯ＝∠ＣＡＯ， ∴∠ＡＣＯ＝∠ＡＥＣ，∴ＡＣ＝ＡＥ， ８分!!!!!!!! ∵ＡＣ＝ＣＤ，∴ＡＥ＝ＣＤ． １０分!!!!!!!!!!! 方法三：如解图，连接 ＡＤ，ＯＤ， ∵ＡＣ＝ＤＢ， ∴ ) ＡＣ＝ ) ＢＤ， ∴∠ＡＤＣ＝∠ＤＡＢ， ２分!!!!!!!!!!!!! ∴ＣＤ∥ＡＢ， ∴∠ＡＥＣ＝∠ＤＣＯ， ４分!!!!!!!!!!!!! ∵ＡＣ＝ＣＤ，ＡＯ＝ＤＯ， ∴ＣＯ⊥ＡＤ， ∴∠ＡＣＯ＝∠ＤＣＯ， ６分!!!!!!!!!!!!! ∴∠ＡＣＯ＝∠ＡＥＣ，∴ＡＣ＝ＡＥ， ８分!!!!!!!! ∵ＡＣ＝ＣＤ，∴ＡＥ＝ＣＤ． １０分!!!!!!!!!!! ２４．（１）①证明：∵把 ＢＡ顺时针方向旋转 ６０°至 ＢＥ， ∴ＢＡ＝ＢＥ，∠ＡＢＥ＝６０°， １分!!!!!!!!!!! ∵在等边△ＢＣＤ中， ∴ＤＢ＝ＢＣ，∠ＤＢＣ＝６０°， ∴∠ＤＢＡ＝∠ＤＢＣ＋∠ＦＢＡ＝６０°＋∠ＦＢＡ， ∵∠ＣＢＥ＝６０°＋∠ＦＢＡ， ∴∠ＤＢＡ＝∠ＣＢＥ， ２分!!!!!!!!!!!!! ∴△ＢＡＤ≌△ＢＥＣ， ∴ＤＡ＝ＣＥ； ３分!!!!!!!!!!!!!!!! ②判断：∠ＤＥＣ＋∠ＥＤＣ＝９０°． ４分!!!!!!!! 理由：∵ＤＢ＝ＤＣ，ＤＡ⊥ＢＣ，∴∠ＢＤＡ＝１ ２∠ＢＤＣ＝３０°， ∵△ＢＡＤ≌△ＢＥＣ， ∴∠ＢＣＥ＝∠ＢＤＡ＝３０°， ５分!!!!!!!!!!! ∵在等边△ＢＣＤ中，∠ＢＣＤ＝６０°， ∴∠ＤＣＥ＝∠ＢＣＥ＋∠ＢＣＤ＝９０°，∴∠ＤＥＣ＋∠ＥＤＣ＝ ９０°． ６分!!!!!!!!!!!!!!!!!!! （２）分三种情况考虑： ①当点 Ａ在线段 ＤＦ的延长线上时，如解图①，连接 ＡＣ， 由（１）可得，△ＤＣＥ为直角三角形，∴∠ＤＣＥ＝９０°， 当∠ＤＥＣ＝４５°时，∠ＥＤＣ＝９０° －∠ＤＥＣ＝４５°， ∴∠ＥＤＣ＝∠ＤＥＣ，∴ＣＤ＝ＣＥ， 第 ２４题解图① 由（１）得 ＤＡ＝ＣＥ，∴ＣＤ＝ＤＡ．在等边△ＤＢＣ中，ＢＤ＝ ＣＤ， ∴ＢＤ＝ＤＡ＝ＣＤ， ∠ＢＤＣ＝６０°， ∵ＤＡ⊥ＢＣ， ∴∠ＢＤＡ＝∠ＣＤＡ＝１ ２∠ＢＤＣ＝３０°， ７分!!!!!! 在△ＢＤＡ中，ＤＢ＝ＤＡ，∴∠ＢＡＤ＝１８０°－∠ＢＤＡ ２ ＝７５°， 在△ＤＡＣ中，ＤＡ＝ＤＣ，∴∠ＤＡＣ＝１８０°－∠ＡＤＣ ２ ＝７５°， ∴∠ＢＡＣ＝∠ＢＡＤ＋∠ＤＡＣ＝７５°＋７５°＝１５０°； ８分!! ②当点 Ａ在线段 ＤＦ上时，如解图②，连接 ＡＣ， 第 ２４题解图② ∵以 Ｂ为旋转中心，把 ＢＡ顺时针方向旋转 ６０°至 ＢＥ， ∴ＢＡ＝ＢＥ，∠ＡＢＥ＝６０°， 在等边△ＢＤＣ中，ＢＤ＝ＢＣ，∠ＤＢＣ＝６０°， ∴∠ＤＢＣ＝∠ＡＢＥ， ∠ＤＢＣ－∠ＡＢＣ＝∠ＡＢＥ－∠ＡＢＣ， 即∠ＤＢＡ＝∠ＥＢＣ， ∴△ＤＢＡ≌△ＣＢＥ， ∴ＤＡ＝ＣＥ， ９分!!!!!!!!!!!!!!!! 在 Ｒｔ△ＤＦＣ中，∠ＤＦＣ＝９０°， ∴ＤＦ＜ＤＣ， ∵ＤＡ＜ＤＦ，ＤＡ＝ＣＥ， ∴ＣＥ＜ＤＣ， 由②可知△ＤＣＥ为直角三角形                                                                        ， １６　　　 ∴∠ＤＥＣ≠４５°； １０分!!!!!!!!!!!!!! ③当点 Ａ在线段 ＦＤ的延长线上时，如解图③， 同第②种情况可得△ＤＢＡ≌△ＣＢＥ， ∴ＤＡ＝ＣＥ，∠ＡＤＢ＝∠ＥＣＢ， 在等边△ＢＤＣ中，∠ＢＤＣ＝∠ＢＣＤ＝６０°， ∵ＤＡ⊥ＢＣ， ∴∠ＢＤＦ＝∠ＣＤＦ＝１ ２∠ＢＤＣ＝３０°， ∴∠ＡＤＢ＝１８０°－∠ＢＤＦ＝１５０°， ∴∠ＥＣＢ＝∠ＡＤＢ＝１５０°， ∴∠ＤＣＥ＝∠ＥＣＢ－∠ＢＣＤ＝９０°， 当∠ＤＥＣ＝４５°时，∠ＥＤＣ＝９０°－∠ＤＥＣ＝４５°， ∴∠ＥＤＣ＝∠ＤＥＣ， ∴ＣＤ＝ＣＥ， ∴ＡＤ＝ＣＤ＝ＢＤ， １１分!!!!!!!!!!!!!! ∵∠ＡＤＢ＝∠ＡＤＣ＝１５０°， ∴∠ＢＡＤ＝１８０°－∠ＡＤＢ ２ ＝１５°，∠ＣＡＤ＝１８０°－∠ＣＤＡ ２ ＝１５°， ∴∠ＢＡＣ＝∠ＢＡＤ＋∠ＣＡＤ＝３０°， 第 ２４题解图③ 综上所述，∠ＢＡＣ的度数为１５０°或３０°． １２分!!!! ２５．解：（１）把 Ａ（０，４），Ｂ（２，０），Ｃ（－２，０）代入 ｙ＝ａｘ２ ＋ｂｘ ＋ｃ得， ｃ＝４ ４ａ＋２ｂ＋ｃ＝０ ４ａ－２ｂ＋ｃ{ ＝０ ， ２分!!!!!!!!!!!!!! 解得： ａ＝－１ ｂ＝０ ｃ{ ＝４ ， ∴ｙ＝－ｘ２ ＋４； ４分!!!!!!!!!!!!!!! （２）①设直线 ＤＡ得解析式为 ｙ＝ｋｘ＋ｄ（ｋ≠０）， 把 Ａ（０，４），Ｄ（－４，０）代入得， ｄ＝４ －４ｋ＋ｄ{ ＝０，解得： ｋ＝１ ｄ{ ＝４， ∴ｙ＝ｘ＋４， ６分!!!!!!!!!!!!!!!! 设 Ｅ（ｍ，ｍ＋４）， 平移后的抛物线的解析式为：ｙ＝－（ｘ－ｍ）２ ＋ｍ＋４． 把 Ｂ（２，０）代入得：－（２－ｍ）２ ＋ｍ＋４＝０， 解得 ｍ１ ＝５，ｍ２ ＝０（不符合题意，舍去）， ∴Ｅ（５，９）； ８分!!!!!!!!!!!!!!!! ②如解图，连接 ＡＢ，过点 Ｂ作 ＢＬ∥ＡＤ交平移后的抛物 线于点 Ｇ，连接 ＥＧ， ∴四边形 ＡＢＧＥ的面积就是图象 Ａ，Ｂ两点间的部分扫过 的面积． １０分!!!!!!!!!!!!!!!!! 过点 Ｇ作 ＧＫ⊥ｘ轴于点 Ｋ，过点 Ｅ作 ＥＩ⊥ｙ轴于点 Ｉ，直 线 ＥＩ，ＧＫ交于点 Ｈ． 第 ２５题解图 方法一：由点 Ａ（０，４）平移至点 Ｅ（５，９），可知点 Ｂ先向右 平移 ５个单位，再向上平移 ５个单位至点 Ｇ． ∵Ｂ（２，０），∴点 Ｇ（７，５）， １２分!!!!!!!!!! ∴ＧＫ＝５，ＯＢ＝２，ＯＫ＝７， ∴ＢＫ＝ＯＫ－ＯＢ＝７－２＝５， ∵Ａ（０，４），Ｅ（５，９）， ∴ＡＩ＝９－４＝５，ＥＩ＝５， ∴ＥＨ＝７－５＝２，ＨＧ＝９－５＝４， ∴Ｓ四边形ＡＢＧＨ ＝Ｓ矩形ＩＯＫＨ －Ｓ△ＡＯＢ －Ｓ△ＡＥＩ－Ｓ△ＥＨＧ －Ｓ△ＧＢＫ ＝７×９－１ ２ ×２×４－１ ２ ×５×５－１ ２ ×２×４－１ ２ ×５×５ ＝６３－８－２５ ＝３０． ∴图象 Ａ，Ｂ两点间的部分扫过的面积为 ３０． １４分!! 方法二：设直线 ＢＬ的解析式为 ｙ＝ｘ＋ｂ′， 把点 Ｂ（２，０）代入得：２＋ｂ′＝０，ｂ′＝－２， ∴ｙ＝ｘ－２，联 立 ｙ＝ｘ－２ ｙ＝－（ｘ－５）２{ ＋９，解 得： ｘ１ ＝２ ｙ１{ ＝０， ｘ２ ＝７ ｙ２{ ＝５， ∴点 Ｇ（７，５）， １２分!!!!!!!!!!!!!!! ∴ＧＫ＝５，ＯＢ＝２，ＯＫ＝７， ∴ＢＫ＝ＯＫ－ＯＢ＝７－２＝５， ∵Ａ（０，４），Ｅ（５，９）， ∴ＡＩ＝９－４＝５，ＥＩ＝５， ∴ＥＨ＝７－５＝２，ＨＧ＝９－５＝４， ∴Ｓ四边形ＡＢＧＨ ＝Ｓ矩形ＩＯＫＨ －Ｓ△ＡＯＢ －Ｓ△ＡＥＩ－Ｓ△ＥＨＧ －Ｓ△ＧＢＫ ＝７×９－１ ２ ×２×４－１ ２ ×５×５－１ ２ ×２×４－１ ２ ×５×５ ＝６３－８－２５ ＝３０． ∴图象 Ａ，Ｂ两点间的部分扫过的面积为 ３０． １４分                                                            !!