2020年八年级数学下册17微专题特殊平行四边形中的最值问题习题（新版）冀教版

2020年八年级数学下册17微专题特殊平行四边形中的最值问题习题（新版）冀教版

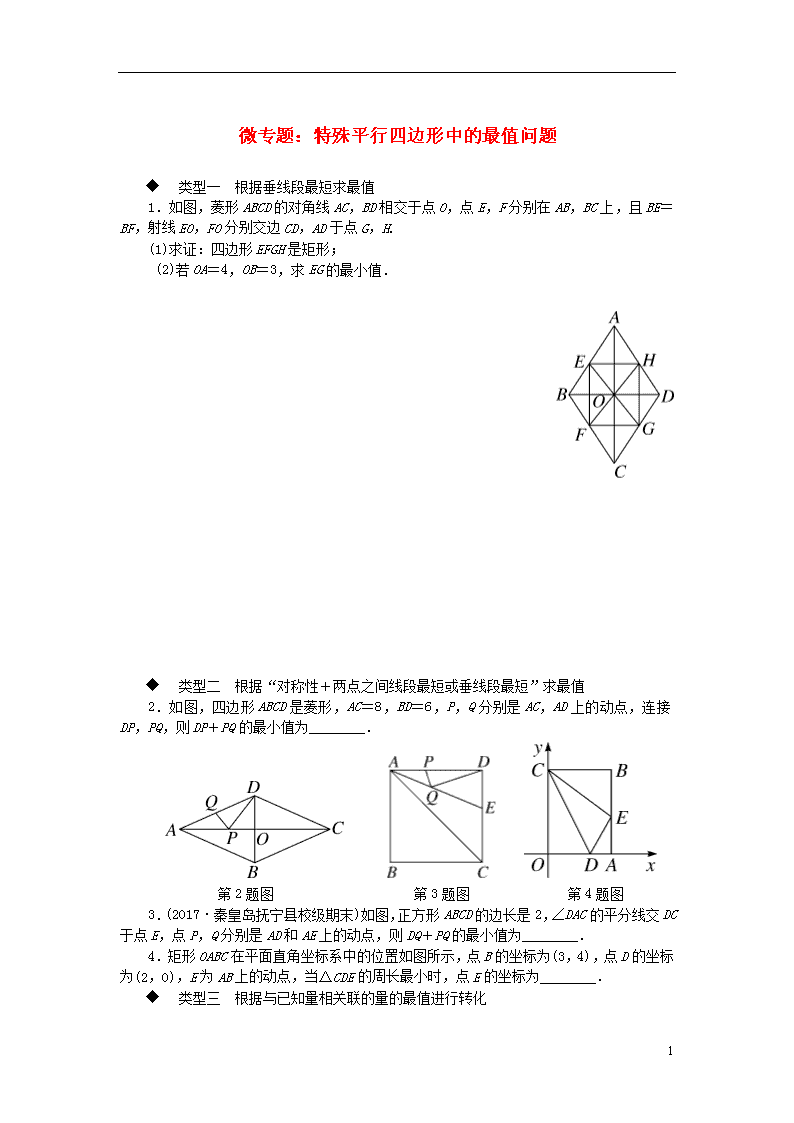
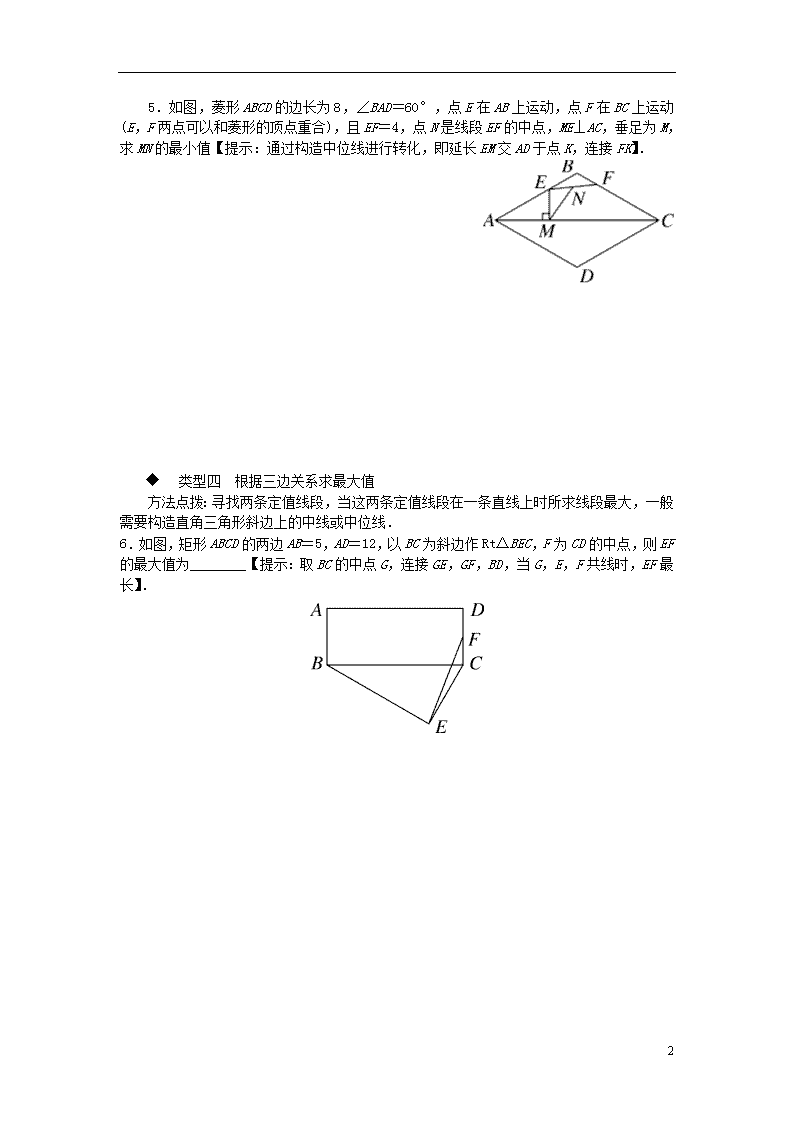
微专题：特殊平行四边形中的最值问题 类型一　根据垂线段最短求最值 ‎1．如图，菱形ABCD的对角线AC，BD相交于点O，点E，F分别在AB，BC上，且BE＝BF，射线EO，FO分别交边CD，AD于点G，H.‎ ‎(1)求证：四边形EFGH是矩形；‎ ‎ (2)若OA＝4，OB＝3，求EG的最小值．‎ 类型二　根据“对称性＋两点之间线段最短或垂线段最短”求最值 ‎2．如图，四边形ABCD是菱形，AC＝8，BD＝6，P，Q分别是AC，AD上的动点，连接DP，PQ，则DP＋PQ的最小值为________．‎ ‎ ‎ 第2题图　 第3题图 第4题图 ‎3．(2017·秦皇岛抚宁县校级期末)如图，正方形ABCD的边长是2，∠DAC的平分线交DC于点E，点P，Q分别是AD和AE上的动点，则DQ＋PQ的最小值为________．‎ ‎4．矩形OABC在平面直角坐标系中的位置如图所示，点B的坐标为(3，4)，点D的坐标为(2，0)，E为AB上的动点，当△CDE的周长最小时，点E的坐标为________．‎ 类型三　根据与已知量相关联的量的最值进行转化 4‎ ‎5．如图，菱形ABCD的边长为8，∠BAD＝60°，点E在AB上运动，点F在BC上运动(E，F两点可以和菱形的顶点重合)，且EF＝4，点N是线段EF的中点，ME⊥AC，垂足为M，求MN的最小值【提示：通过构造中位线进行转化，即延长EM交AD于点K，连接FK】．‎ ‎ ‎ 类型四　根据三边关系求最大值 方法点拨：寻找两条定值线段，当这两条定值线段在一条直线上时所求线段最大，一般需要构造直角三角形斜边上的中线或中位线．‎ 6． 如图，矩形ABCD的两边AB＝5，AD＝12，以BC为斜边作Rt△BEC，F为CD的中点，则EF的最大值为________【提示：取BC的中点G，连接GE，GF，BD，当G，E，F共线时，EF最长】．‎ 4‎ ‎参考答案与解析 ‎1．(1)证明：∵四边形ABCD是菱形，∴OA＝OC，OB＝OD，AB∥CD，AD∥BC，∴∠BAO＝∠DCO.又∵∠AOE＝∠COG，∴△AOE≌△COG(ASA)，∴OE＝OG，同理得OH＝OF，∴四边形EFGH是平行四边形．∵BE＝BF，∠ABD＝∠CBD，OB＝OB，∴△EBO≌△FBO，∴OE＝OF，∴EG＝FH，∴四边形EFGH是矩形．‎ ‎(2)解：∵垂线段最短，∴当OE⊥AB时，OE最小．∵EG＝2OE，∴OE最小时，EG最小．∵OA＝4，OB＝3，∠AOB＝90°，∴AB2＝OA2＋OB2＝25，∴AB＝5，∴OA·OB＝AB·OE，即3×4＝5·OE，解得OE＝.∵EG＝2OE，∴EG＝.故EG的最小值是.‎ ‎ 2.　解析：如图，过点Q作QE⊥AC交AB于点E，则PQ＝PE.∴DP＋PQ＝DP＋PE，当点D，P，E三点共线的时，DP＋PQ＝DP＋PE＝DE最小，DE即为所求．当DE⊥AB时，DE最小．∵AC＝8，BD＝6，∴OA＝4，OB＝3，∴在Rt△AOB中，AB＝＝5.∵S菱形ABCD＝AC·BD＝AB·DE.∴×8×6＝5·DE.∴DE＝.∴DP＋PQ的最小值为.‎ ‎3.　 解析：作D关于AE的对称点D′，过D′作D′P′⊥AD于P′，D′P′交AE于点Q，易知D′落在AC上，且AD′＝AD＝2，且此时DQ＋PQ的值最小，即为D′P′的长度．∵四边形ABCD是正方形，∴∠DAD′＝45°，∴AP′＝P′D′，∴在Rt△AP′D′中，P′D′2＋AP′2＝AD′2＝4.∵AP′＝P′D′，∴P′D′＝，即DQ＋PQ的最小值为.‎ ‎4．(3，1)　解析：∵点C，点D为定点，∴CD的长为定值．∵△CDE的周长＝CD＋DE＋CE，∴要使△CDE的周长最小，就要使DE＋CE最小．作点D关于直线AB的对称点H，连接CH，交AB于点E，则此时△CDE的周长最小．由对称性可得AD＝AH.∵四边形OABC是矩形，B(3，4)，∴OC＝4，OA＝3.∵OD＝2，∴AD＝1＝AH，∴H(4，0)．设直线CH的表达式为y＝kx＋b，则解得故直线CH的表达式为y＝－x＋4.当x＝3时，y＝－3＋4＝1，∴点E的坐标为(3，1)．‎ ‎5．解：如图，延长EM交AD于K，连接FK.∵四边形ABCD是菱形，∴∠BAC＝∠DAC.∵EM⊥AC，∴EM＝MK，即点M为EK的中点．又∵点N是EF的中点，∴MN＝KF，∴当KF⊥AD时，KF的值最小，此时MN最小．连接BD.∵∠BAD＝60°，AB＝AD＝8，∴△ABD是等边三角形，∴S△ABD＝16.∵S菱形ABCD＝2S△ABD，∴AD·FK＝2×16，∴8·FK＝32，∴FK＝4，∴MN的最小值为KF＝2.‎ ‎ ‎ 4‎ ‎6.　解析：如图，取BC的中点G，连接GE，GF，BD.∵∠BEC＝90°，点G为BC的中点，∴GE＝BC＝6.∵AB＝5，AD＝12，∠A＝90°，∴BD＝＝13.∵点G为BC的中点，点F为CD的中点，∴GF＝BD＝.由三角形三边关系定理知GE＋GF＞EF，∴当点E，G，F三点共线的时候，EF取得最大值为GE＋GF＝6＋＝.‎ 4‎