八年级上数学课件- 11-2-1 三角形的内角 课件（共39张PPT）_人教新课标

八年级上数学课件- 11-2-1 三角形的内角 课件（共39张PPT）_人教新课标

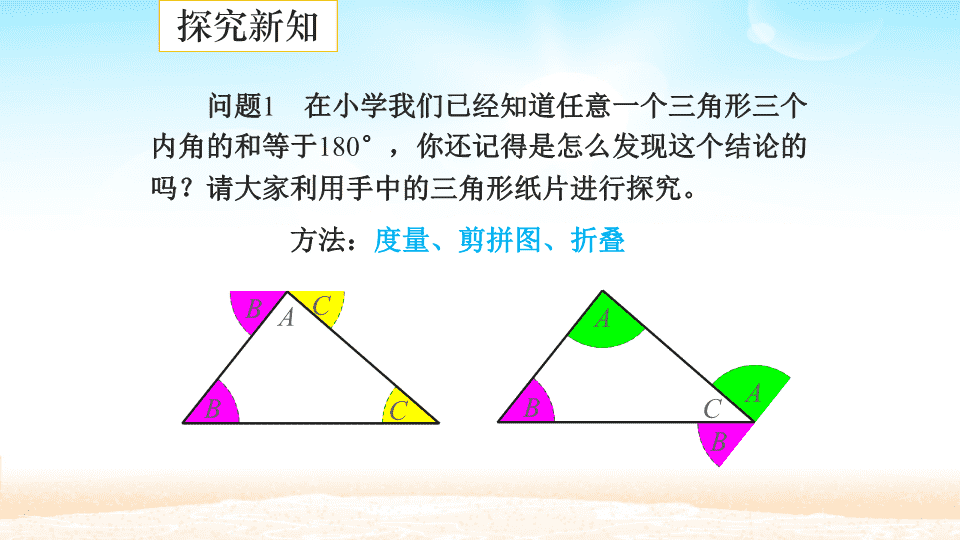
三角形的内角 第一课时 学习目标： 1.探索并证明三角形内角和定理。 2.能运用三角形内角和定理解决简单问题。 学习重点： 探索并证明三角形内角和定理，体会证明的必要性。 目标重点 方法：度量、剪拼图、折叠 B B C C A A AB B C 　　问题1　在小学我们已经知道任意一个三角形三个 内角的和等于180°，你还记得是怎么发现这个结论的 吗？请大家利用手中的三角形纸片进行探究。 探究新知 A A B B C A B BC C 方法：度量、剪拼图、折叠 　　问题1　在小学我们已经知道任意一个三角形三个 内角的和等于180°，你还记得是怎么发现这个结论的 吗？请大家利用手中的三角形纸片进行探究。 方法：度量、剪拼图、折叠 　　问题1　在小学我们已经知道任意一个三角形三个 内角的和等于180°，你还记得是怎么发现这个结论的 吗？请大家利用手中的三角形纸片进行探究。 A B C 演示 1 2 3 　　追问1　运用度量的方法，得出的三个内角的和都 是180°吗？为什么？ 测量可能会有误差。　　　 探究追问 　　追问2　通过度量、剪拼图或折叠的方法验证了手 中的三角形纸片的三个内角和等于180°，但我们手中 的三角形只是所有三角形中有限的几个，而形状不同的 三角形有无数多个，我们如何能得出“所有的三角形的 三个内角的和都等于180°。”这个结论呢？ 需要通过推理的方法去证明。　　　 　　问题2　 你能从以上的操作过程中受到启发，想出证明 “三角形内角和等于180°”的方法吗？ 探索证明 　　追问1　在下图中，∠B和∠C分别拼在∠A的左右， 三个角合起来形成一个平角，出现了一条过点A的直线l， 直线l与边BC有什么位置关系？ 直线l与边BC平行。　　　 B B C CA l 追问2　在操作过程中，我们发现了与边BC平行的 直线l，由此，你又能受到什么启发？你能发现证明 “三角形内角和等于180°”的思路吗？ 通过添加与边BC 平行的辅助线l，利用 平行线的性质和平角 的定义即可证明结论。　　　 B B C CA l 证明：过点A作直线l，使l∥BC。 ∵　l∥BC， ∴　∠2=∠4， ∠3=∠5 （两直线平行，内错角相等）。 追问3　结合下图，你能写出已知、求证和证明吗？ 已知：△ABC。求证：∠A+∠B+∠C=180°。 A B C2 4 1 5 3 　l 追问3　结合下图，你能写出已知、求证和证明吗？ 已知：△ABC。求证：∠A+∠B+∠C=180°。 A B C2 4 1 5 3 　l 证明：∵　∠1+∠4+∠5=180° （平角定义）， ∴　∠A+∠B+∠C=180° （等量代换）。 三角形内角和定理： 三角形的内角和等于180°。 即在△ABC中，∠A+∠B+∠C=180°。 探索归纳 　追问4　通过前面的操作和证明过程，你能受到什 么启发？你能用其他方法证明此定理吗？ C A B 1 2 3 4 5 l 自我尝试 　追问4　通过前面的操作和证明过程，你能受到什 么启发？你能用其他方法证明此定理吗？ C A B 1 2 34 5 l P 6 m 　追问4　通过前面的操作和证明过程，你能受到什 么启发？你能用其他方法证明此定理吗？ C A B 1 2 3 4 5 l P 6 m n 　追问4　通过前面的操作和证明过程，你能受到什 么启发？你能用其他方法证明此定理吗？ C A B 1 2 3 4 5 l P 6 m n 　　例1　如图，在△ABC中，∠BAC=40°，∠B= 75°，AD是△ABC的角平分线。求∠ADB的度数。 C B D A 例题学习 解：由∠BAC=40°，AD是△ABC的角平分线， 得 在△ABD中， ∠ADB=180°-∠B-∠BAD =180°-75°-20° =85。 1 20 2 BAD BAC     　　例2　如图，C岛在A岛的北偏东50°方向，B岛 在A岛的北偏东80°方向，C岛在B岛的北偏西40°方 向。从B岛看A，C两岛的视角∠ABC是多少度？从C 岛看A，B两岛的视角∠ACB呢？ 北 北C A B D E A D B C E 北 北∵AD∥BE ∴∠DAB﹢∠ABE＝180° ∴∠ABE＝180°－∠DAB ＝180°－80°＝100° 在△ABC中，∠C＝180°－∠CAB－∠ABC ＝180°－30°－60°＝90° ∴∠ABC＝∠ABE－∠CBE ＝100°－40°＝60° 解：∠CAB=∠BAD－∠CAD=80°－50°=30° 　练习1　如图，说出各图中∠1的度数。　　 80° 50° 1 30° 105° 1 22° 1 （1） （2） （3） 课堂练习 　　练习2　如图，从A处观测C处的仰角∠CAD= 30°，从B处观测C处的仰角∠CBD=45°。从C处观 测A，B两处的视角∠ACB是多少？　　 A B D C （1）本节课学习了哪些主要内容？ （2）为什么要用推理的方法证明“三角形的内角和 等于180°”？ （3）你是怎么找到三角形内角和定理的证明思路的？ 课堂小结 三角形的内角 第二课时 学习目标： 1.探索并掌握直角三角形的两个锐角互余。 2.掌握有两个角互余的三角形是直角三角形。 学习重点： 探索并掌握直角三角形的两个锐角互余。 目标重点 问题1　 在△ABC中，∠A=60°，∠B=30°，∠C等于 多少度？你用了什么知识解决的？ A B C 探究新知 三角形的内角和等于180°。∠C=90° 问题2　 在△ABC中，若∠C=90°，你能求出∠A， ∠B的度数吗？为什么？你能求出∠A+∠B的度数吗？ 利用上面的结果，你能得出什么结论？ 　　直角三角形的两个锐角互余。　　 A B C 探究归纳 　　直角三角形可以用符号“Rt△”表示， 直角三角形ABC可以写成Rt△ABC。 在Rt△ABC中， ∵　∠C=90°， ∴　∠A+∠B=90°。　　 　　问题3　此性质的几何推理格式该怎样表示？ A B C 　　例3　如图，∠C=∠D=90°，AD，BC相交于点E， ∠CAE与∠DBE有什么关系？为什么？ 　　分析：两个角的关系是 什么？这两个角分别在什么 三角形中？你如何验证自己 的想法？ 例题学习 C D E A B 解：在Rt△AEC中， ∵　∠C=90°， ∴　∠CAE+∠AEC=90° （直角三角形两锐角互余）。 在Rt△BDE中， ∵　∠D=90°， 　　例3　如图，∠C=∠D=90°，AD，BC相交于点E， ∠CAE与∠DBE有什么关系？为什么？ C D E A B 解：∴　∠DBE+∠BED=90° （直角三角形两锐角互余）。 ∵　∠AEC=∠BED （对顶角相等）， ∴　∠CAE=∠DBE （等角的余角相等）。 　　例3　如图，∠C=∠D=90°，AD，BC相交于点E， ∠CAE与∠DBE有什么关系？为什么？ C D E A B 　　问题4　我们知道，如果一个三角形是直角三角形， 那么这个三角形有两个角互余。反过来，你能得出什么 结论？这个结论成立吗？如何验证你的想法？ 　　利用三角形内角和定理可得： 有两个角互余的三角形是直角三角形。　　 归纳总结 　　问题5　类比性质的几何推理格式，判定的几何推 理格式又该怎样表示？ 推理格式： 在Rt△ABC中， ∵　∠A+∠B=90°， ∴　△ABC是直角三角形。 A B C 相等； 同角的余角相等。 　　练习　如图，∠ACB=90°，CD⊥AB，垂足为D， ∠ACD与∠B有什么关系？为什么？ D A B C 课堂练习 　　变式1　若∠ACD=∠B，∠ACB=90°，则CD是 △ACB的高吗？为什么？ 　　是； 　　有两个角互余的三角形 是直角三角形。 D A B C 　　变式2　若∠ACD=∠B，CD⊥AB，△ACB为直角 三角形吗？为什么？ 　　是； 　　有两个角互余的三角形 是直角三角形。 D A B C 　　变式3　如图，若∠C=90°，∠AED=∠B，△ADE 是直角三角形吗？为什么？ 　　是。 　　有两个角互余的三角形 是直角三角形。 （证明过程略）。 D E A B C （1）本节课学习了哪些主要内容？ （2）你是如何探索直角三角形的性质与判定的？它们 是怎么叙述的？它们有什么区别与联系？ （3）利用直角三角形的性质与判定分别可以解决哪些 问题？ 课堂小结 谢 谢