八年级数学上册第15章轴对称图形和等腰三角形15-4角的平分线（第2课时）课件（新版）沪科版

八年级数学上册第15章轴对称图形和等腰三角形15-4角的平分线（第2课时）课件（新版）沪科版

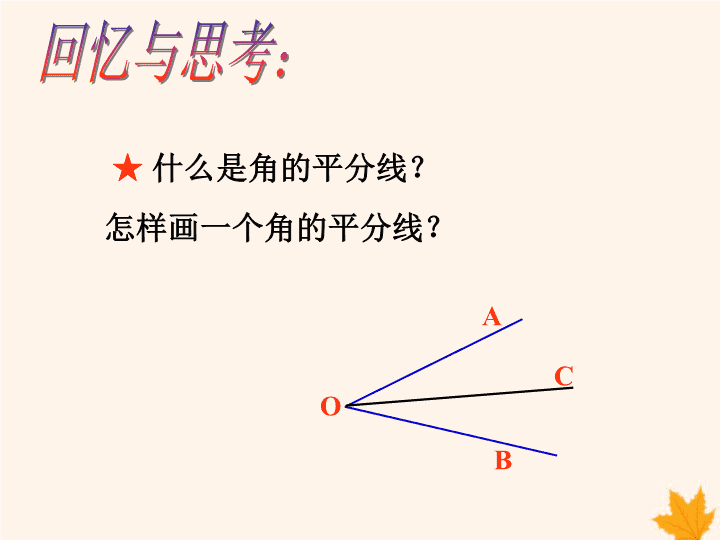
15.4 角的平分线 第2课时 角平分线的性质 第十五章 ★ 什么是角的平分线？ 怎样画一个角的平分线？ B O A C 　　２．分别以Ｍ，Ｎ为 圆心．大于 ＭＮ的长为 半径作弧．两弧在∠AOB 的内部交于Ｃ． 2 1 如何用尺规作角的平分线？ 　　１．以Ｏ为圆心，适当 长为半径作弧，交ＯＡ于Ｍ， 交ＯＢ于Ｎ． ３．作射线OC．则射线ＯＣ即为所求． 角平分线是以一个角的顶点为端点的一条射线，它 把这个角分成两个相等的角. 探究 如图，在∠AOB的平分线OC上任取一点P， 作PD⊥OA ， PE⊥OB ， 垂足分别为点D， E， 试问PD与PE相等吗？ 你能证明吗？ 将∠AOB 沿OC 对折，我发 现PD与PE 重合， 即PD与PE 相等. ∵ PD⊥OA， PE⊥OB， ∴ ∠PDO =∠PEO = 90°. 在△PDO和△PEO中， ∵ ∠PDO =∠PEO， ∠DOP =∠EOP， OP = OP， ∴ △PDO≌△PEO. ∴ PD = PE. 我们来证明这个结论. 由此得到角平分线的性质定理： 角的平分线上的点到角两边的距离相等. 动脑筋 角的内部到角的两边距离相等的点在这个角 的平分线上吗？ 如图，点P 在∠AOB 的内部， 作PD⊥OA， PE⊥OB， 垂足分别为点D，E. 若PD= PE， 那 么点P在∠AOB的平分线上吗？ 在Rt△PDO和Rt△PEO中， ∵ OP = OP，PD = PE， ∴ Rt△PDO≌Rt△PEO. ∵ PD⊥OA， PE⊥OB， ∴ ∠PDO =∠PEO = 90°. 如图，过点O，P作射线OC. ∴ ∠AOC =∠BOC. ∴ OC是∠AOB的平分线，即点P在∠AOB的平分线OC上. 由此得到角平分线的性质定理的逆定理： 角的内部到角两边距离相等的点在角的平分线上. 举 例 例1 如图，∠BAD =∠BCD = 90°，∠1=∠2. （1）求证：点B在∠ADC的平分线上； （2）求证：BD是∠ABC的平分线. 证明： 在△ABC中， ∵ ∠1=∠2， ∴ BA = BC. 又 BA⊥AD， BC⊥CD， ∴ 点B在∠ADC的平分线上. （1）求证：点B在∠ADC的平分线上； 证明： 在Rt△BAD和Rt△BCD中， ∵ BA = BC， BD = BD， ∴ Rt△BAD≌Rt△BCD. ∴ ∠ABD =∠CBD. ∴ BD是∠ABC的平分线. （2）求证：BD是∠ABC的平分线. （要求：各小组长组织好本组成 员对合作探究部分先进行讨论） 合 作 探 究 要求： ⑴展示的同学要注意解题格式，书写要认真、规范； 点评的同学要分析题意，条理清晰。 ⑵非展示、点评同学、小组继续讨论解决组内疑惑、 对展示点评进行质疑。 交流内容 展示小组 点评小组 合作交流 1 1 8 合作交流 2 2 7 合作交流 3 3 6 只 当 观 众 的 人 永 远 领 不 到 金 牌 合作交流 1 展示小组 点评小组 1 8 探讨△ABC的三条角平分线的交点与三边的距离 关系,并说明理由。 合作交流 2 展示小组 点评小组 3 6 如图,AD是∠BAC的平分线,DE⊥AB于E,DF⊥AC 于F,且DB=DC,求证:BE=CF E D CA F B 如图,已知E是∠AOB的平分线上的 一点,EC⊥OA,ED⊥OB,垂足分别为C、 D，你能得到哪些结论？并证明你 的结论。 O C D B E P A 角的内部到角两边距离相等的点在角的平分线上. 用数学语言表示为： 角的平分线上的点到角两边的距离相等. 从这节课中你有哪些收获？