- 2021-11-01 发布 |
- 37.5 KB |
- 5页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020八年级数学上册 第12章 三角形全等的判定 12
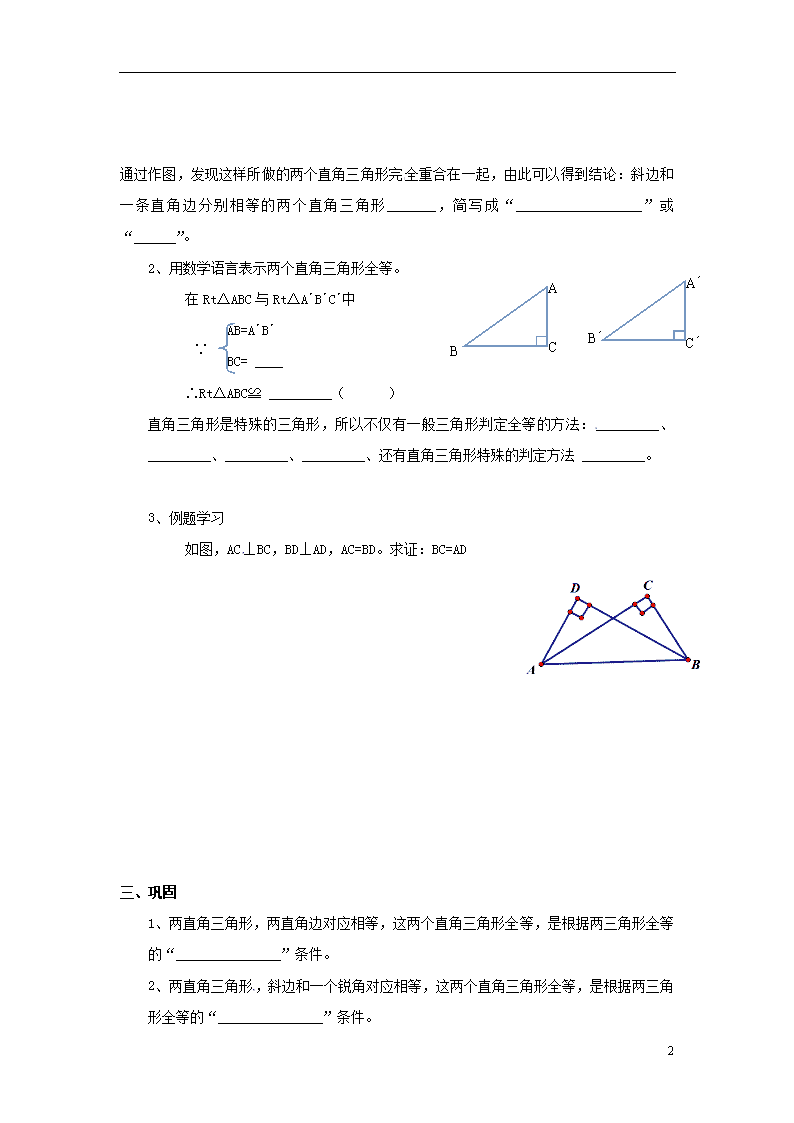
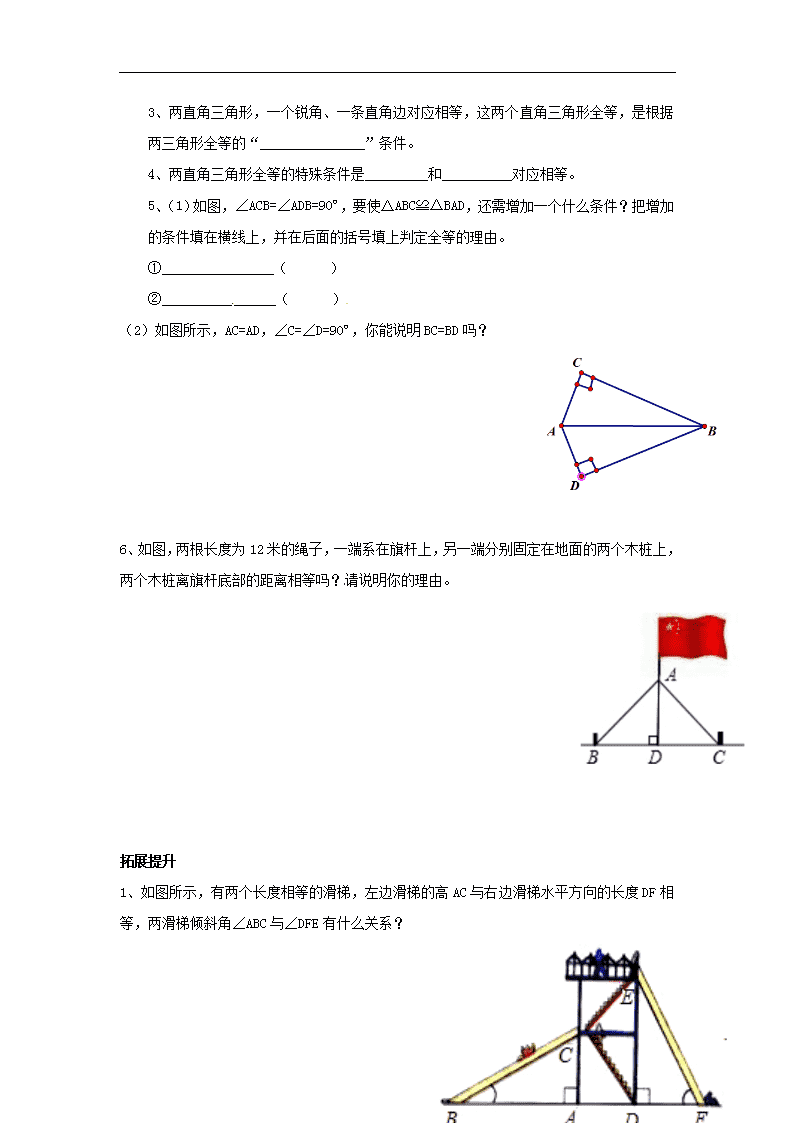
课题:12.2.4 三角形全等的判定(HL) 【学习目标】 1、探索和了解直角三角形全等的条件:“斜边、直角边”; 2、会运用“斜边、直角边”判定两个直角三角形全等。 【学习重点】 探究直角三角形全等的条件 【学习难点】 灵活运用三角形全等的条件证明 【学习过程】 一、知识链接 复习旧知 判定三角形全等的方法有________________、____________、__________、___________。 二、自主学习 阅读课本P41-P43,完成下列问题 1、探究学习 探究1:对于两个直角三角形,除了直角相等的条件,还要满足几个条件,这两个三角形就全等了? 探究2: 1、已知任意RtΔABC,∠C = 90º,再画RtΔA´B´C´,使∠C´=∠C=90º,A´B´=AB,B´C´=BC。把画好的RtΔA´B´C´剪下来,放到RtΔABC上,它们全等吗? 5 通过作图,发现这样所做的两个直角三角形完全重合在一起,由此可以得到结论:斜边和一条直角边分别相等的两个直角三角形_______,简写成“__________________”或“______”。 A B C A´ B´ C´ 2、用数学语言表示两个直角三角形全等。 在RtΔABC与RtΔA´B´C´中 ∵ AB=A´B´ BC= ____ ∴RtΔABC≌ _________( ) 直角三角形是特殊的三角形,所以不仅有一般三角形判定全等的方法:_________、_________、_________、_________、还有直角三角形特殊的判定方法 _________。 3、例题学习 如图,AC⊥BC,BD⊥AD,AC=BD。求证:BC=AD 三、巩固 1、 两直角三角形,两直角边对应相等,这两个直角三角形全等,是根据两三角形全等的“_______________”条件。 2、 两直角三角形,斜边和一个锐角对应相等,这两个直角三角形全等,是根据两三角形全等的“_______________”条件。 5 1、 两直角三角形,一个锐角、一条直角边对应相等,这两个直角三角形全等,是根据两三角形全等的“_______________”条件。 2、 两直角三角形全等的特殊条件是_________和__________对应相等。 3、 (1)如图,∠ACB=∠ADB=90º,要使ΔABC≌ΔBAD,还需增加一个什么条件?把增加的条件填在横线上,并在后面的括号填上判定全等的理由。 ①________________( ) ②________________( ) (2) 如图所示,AC=AD,∠C=∠D=90º,你能说明BC=BD吗? 6、 如图,两根长度为12米的绳子,一端系在旗杆上,另一端分别固定在地面的两个木桩上,两个木桩离旗杆底部的距离相等吗?请说明你的理由。 拓展提升 1、 如图所示,有两个长度相等的滑梯,左边滑梯的高AC与右边滑梯水平方向的长度DF相等,两滑梯倾斜角∠ABC与∠DFE有什么关系? 5 2、如图1,E、F分别为线段AC上的两个动点,且DE⊥AC于E点,BF⊥AC于F点, 若AB=CD,AF=CE,BD交AC于M点。(1)求证:MB=MD,ME=MF;(2)当E、F两点移动至图2所示的位置时,其余条件不变,上述结论是否成立?若成立,给予证明。 四、 知识归纳 5 判定三角形全等的方法有 、 、 、 . 判定直角三角形全等除了具有一般三角形全等的判定方法外、还有特殊的判定方法是 . 课后反思:_____________________________________________________ 5查看更多