人教版八年级数学上册同步测试题及答案 (5)

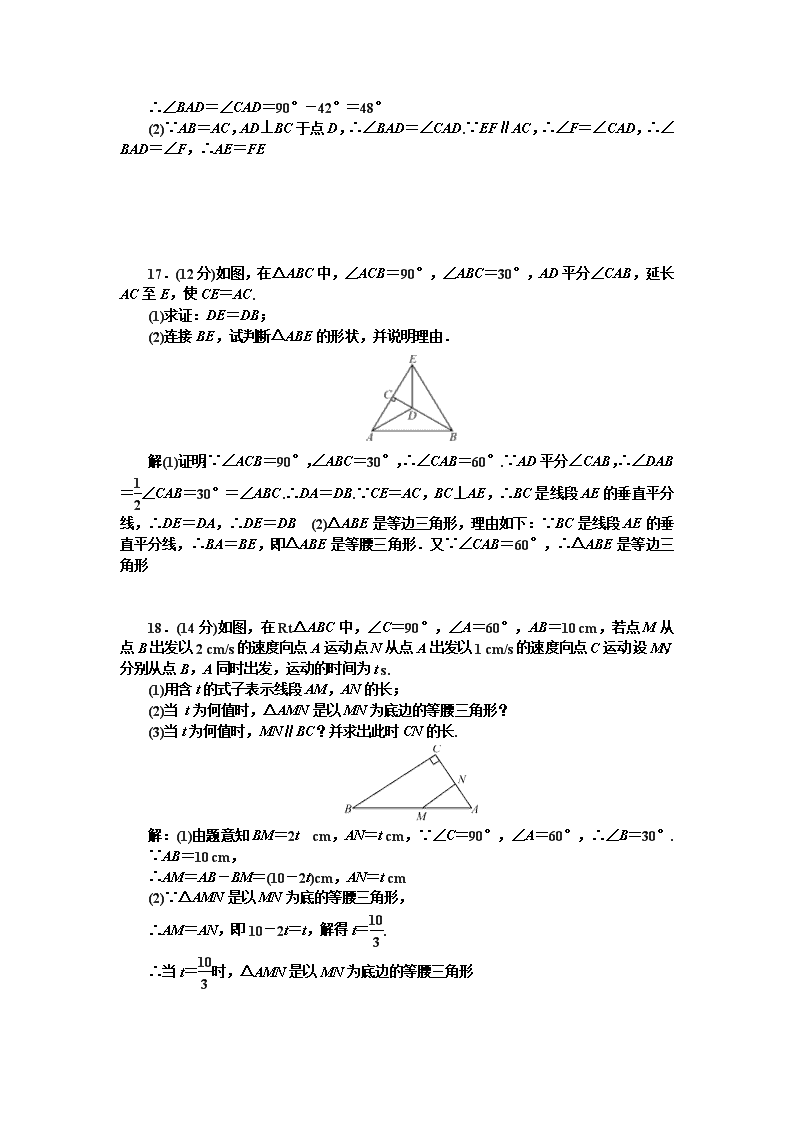
人教版八年级数学上册同步测试题及答案 (5)

检测内容：13.3－13.4 得分________ 卷后分________ 评价________ 一、选择题(每小题 4 分，共 32 分) 1．在△ABC 中，AB＝AC，∠B＝70°，则∠A 的度数是( D ) A．70° B．55° C．50° D．40° 2．若等腰三角形的周长为 10 cm，其中一边长为 2 cm，则该等腰三角形的底边长为( A ) A．2 cm B．6 cm C．2 cm 或 6 cm D．以上全错 3．如图，在△ABC 中，点 D 在 BC 上，若 AD＝BD＝DC，则∠BAC 等于( C ) A．60° B．80° C．90° D．100° 第 3 题图 第 4 题图 4．如图是屋架设计图的一部分，点 D 是斜梁 AB 的中点，立柱 BC，DE 垂直于横梁 AC，AB＝6 m，∠A＝30°，则 DE 等于( A ) A．1.5 m B．2 m C．2.5 m D．3 m 5．如图，E 是等边△ABC 中 AC 边上的点，∠1＝∠2，BE＝CD，则△ADE 的形状是 ( B ) A．等腰三角形 B．等边三角形 C．不等边三角形 D．不能确定形状 第 5 题图 第 6 题图 6．如图，在等边△ABC 中，D 是 AB 的中点，DE⊥AC 于点 E，EF⊥BC 于点 F，已 知 AB＝8，则 BF 的长为( C ) A．3 B．4 C．5 D．6 7．(包头中考)如图，在△ABC 中，AB＝AC，△ADE 的顶点 D，E 分别在 BC，AC 上， 且∠DAE＝90°，AD＝AE.若∠C＋∠BAC＝145°，则∠EDC 的度数为( D ) A．17.5° B．12.5° C．12° D．10° 第 7 题图 第 8 题图 8．如图，等腰三角形 ABC 的底边 BC 长为 4，面积是 16，腰 AC 的垂直平分线 EF 分 别交 AC，AB 边于 E，F 点，若点 D 为 BC 边的中点，点 M 为线段 EF 上一动点，则△CDM 周长的最小值为( D ) A．7 B．8 C．9 D．10 二、填空题(每小题 4 分，共 24 分) 9．如图，在△ADC 中，B 是 AC 上一点，AD＝BD＝BC，若∠C＝25°，则∠ADB＝ __80°__． 第 9 题图 第 10 题图 10．(白银中考)将一张长方形纸片折叠成如图所示的图形，若 AB＝6 cm，则 AC＝ __6__cm. 11．(2019·成都)如图，在△ABC 中，AB＝AC，点 D，E 都在边 BC 上，∠BAD＝∠CAE， 若 BD＝9，则 CE 的长为__9__． 第 11 题图 第 12 题图 12．如图，在△ABC 中，AF 平分∠BAC，AC 的垂直平分线交 BC 于点 E，∠B＝67°， ∠FAE＝19°，则∠C＝__25__度． 13．如图，在等边△ABC 中，BD＝CE，AD 与 BE 交于点 P，AQ⊥BE，垂足为 Q， PD＝2，PQ＝6，则 BE 的长为__14__． 第 13 题图 第 14 题图 14．如图，在等腰△ABC 中，AB＝AC，∠BAC＝120°，AD⊥BC 于点 D，点 P 是 BA 延长线上一点，点 O 是线段 AD 上一点，OP＝OC，下面的结论：①∠APO＋∠DCO＝30°； ②∠APO＝∠DCO；③△OPC 是等边三角形；④AB＝AO＋AP.其中正确的序号是__①③④ __． 三、解答题(共 44 分) 15．(8 分)如图，一艘轮船以 15 海里/小时的速度由南向北航行，在 A 处测得小岛 P 在 北偏西 15°方向上，2 小时后，轮船在 B 处测得小岛 P 在北偏西 30°方向上，在小岛 P 周 围 18 海里内有暗礁，若轮船继续向前航行，有无触礁的危险？ 解：过点 P 作 PC⊥AB，垂足为 C，∵∠PAB＝15°，∠PBC＝30°，∴∠APB＝∠PBC －∠PAB＝30°－15°＝15°.∴PB＝BA.由题意知 AB＝15×2＝30(海里)，∴PB＝30 海 里．在 Rt△PBC 中，∵∠PBC＝30°，∴PC＝1 2 PB＝15 海里．∴PC<18 海里．∴轮船继 续向前航行有触礁的危险 16．(10 分)(2019·重庆)如图，在△ABC 中，AB＝AC，AD⊥BC 于点 D. (1)若∠C＝42°，求∠BAD 的度数； (2)若点 E 在边 AB 上，EF∥AC 交 AD 的延长线于点 F.求证：AE＝FE. 解：(1)∵AB＝AC，AD⊥BC 于点 D，∴∠BAD＝∠CAD，∠ADC＝90°，又∠C＝42°， ∴∠BAD＝∠CAD＝90°－42°＝48° (2)∵AB＝AC，AD⊥BC 于点 D，∴∠BAD＝∠CAD.∵EF∥AC，∴∠F＝∠CAD，∴ ∠BAD＝∠F，∴AE＝FE 17．(12 分)如图，在△ABC 中，∠ACB＝90°，∠ABC＝30°，AD 平分∠CAB，延长 AC 至 E，使 CE＝AC. (1)求证：DE＝DB； (2)连接 BE，试判断△ABE 的形状，并说明理由． 解：(1)证明：∵∠ACB＝90°，∠ABC＝30°，∴∠CAB＝60°.∵AD 平分∠CAB， ∴∠DAB＝1 2 ∠CAB＝30°＝∠ABC.∴DA＝DB.∵CE＝AC，BC⊥AE，∴BC 是线段 AE 的垂直平分线，∴DE＝DA，∴DE＝DB (2)△ABE 是等边三角形，理由如下：∵BC 是线 段 AE 的垂直平分线，∴BA＝BE，即△ABE 是等腰三角形．又∵∠CAB＝60°，∴△ABE 是等边三角形 18．(14 分)如图，在 Rt△ABC 中，∠C＝90°，∠A＝60°，AB＝10 cm，若点 M 从 点 B 出发以 2 cm/s 的速度向点 A 运动，点 N 从点 A 出发以 1 cm/s 的速度向点 C 运动，设 M，N 分别从点 B，A 同时出发，运动的时间为 t s. (1)用含 t 的式子表示线段 AM，AN 的长； (2)当 t 为何值时，△AMN 是以 MN 为底边的等腰三角形？ (3)当 t 为何值时，MN∥BC？并求出此时 CN 的长. 解：(1)由题意知 BM＝2t cm，AN＝t cm，∵∠C＝90°，∠A＝60°，∴∠B＝30°. ∵AB＝10 cm， ∴AM＝AB－BM＝(10－2t)cm，AN＝t cm (2)∵△AMN 是以 MN 为底的等腰三角形， ∴AM＝AN，即 10－2t＝t，解得 t＝10 3 . ∴当 t＝10 3 时，△AMN 是以 MN 为底边的等腰三角形 (3)∵∠C＝90°，∠A＝60°，∴∠B＝30°，AC＝1 2 AB＝5 cm.∵MN∥BC，∴∠NMA ＝30°，∠MNA＝90°，∴AN＝1 2 AM，∴t＝1 2 (10－2t)，解得 t＝5 2 ，∴当 t＝5 2 时，MN∥BC， CN＝5－5 2 ×1＝5 2 cm