- 2021-11-01 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学华东师大版八年级上册教案13-2 三角形全等的判定 第3课时
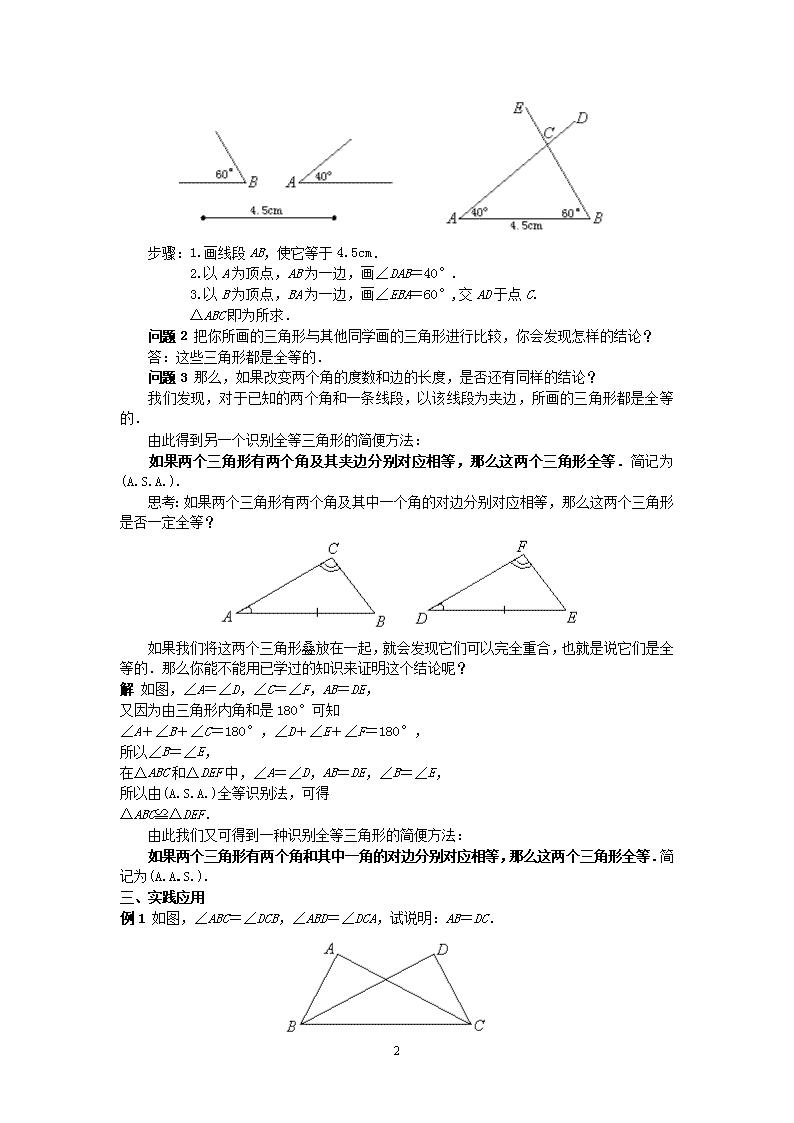
1 13.2 三角形全等的判定 第 3 课时 教学目标 【知识与能力】 1.掌握“已知两角及一边画三角形”的方法. 2.能说出(A.S.A.)全等识别法:如果两个三角形有两个角及其夹边分别对应相等,那么这两 个三角形全等.并能利用它进行简单的应用. 3.能说出(A.A.S.)全等识别法:如果两个三角形有两个角和其中一角的对边分别对应相等, 那么这两个三角形全等.并能利用它进行简单的应用. 【过程与方法】 通过画图、实验、发现、应用的过程教学,使学生体会探索发现问题的过程,经历自己探索 出 A.A.S.的三角形全等识别法及其应用. 【情感态度价值观】 通过积极参与探索,运用观察、归纳、推理等手段发现两个三角形全等的识别法(A.S.A.) 和(A.A.S.),从中感受研究数学的乐趣. 教学重难点 【教学重点】 三角形全等的识别法 A.S.A.和 A.A.S.及其应用. 【教学难点】 利用三角形全等的识别法,冲撞说明角相等或线段相等. 课前准备 无 教学过程 一、创设情境 1.通过前面的学习,你是否能说出证明两个三角形全等有哪些方法? 2.如果知道两个三角形的两个角及一条边分别对应相等,那么这两个角及一条边的位置 情况如何?这样的两个三角形是否全等? 二、探究归纳 问题 1 已知两个角和一条线段,以这两个角为内角,以这条线段为两个角的夹边,画一个 三角形. 2 步骤:1.画线段 AB,使它等于 4.5cm. 2.以 A 为顶点,AB 为一边,画∠DAB=40°. 3.以 B 为顶点,BA 为一边,画∠EBA=60°,交 AD 于点 C. △ABC 即为所求. 问题 2 把你所画的三角形与其他同学画的三角形进行比较,你会发现怎样的结论? 答:这些三角形都是全等的. 问题 3 那么,如果改变两个角的度数和边的长度,是否还有同样的结论? 我们发现,对于已知的两个角和一条线段,以该线段为夹边,所画的三角形都是全等的. 由此得到另一个识别全等三角形的简便方法: 如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全等.简记为 (A.S.A.). 思考:如果两个三角形有两个角及其中一个角的对边分别对应相等,那么这两个三角形 是否一定全等? 如果我们将这两个三角形叠放在一起,就会发现它们可以完全重合,也就是说它们是全 等的.那么你能不能用已学过的知识来证明这个结论呢? 解 如图,∠A=∠D,∠C=∠F,AB=DE, 又因为由三角形内角和是 180°可知 ∠A+∠B+∠C=180°,∠D+∠E+∠F=180°, 所以∠B=∠E, 在△ABC 和△DEF 中,∠A=∠D,AB=DE,∠B=∠E, 所以由(A.S.A.)全等识别法,可得 △ABC≌△DEF. 由此我们又可得到一种识别全等三角形的简便方法: 如果两个三角形有两个角和其中一角的对边分别对应相等,那么这两个三角形全等.简 记为(A.A.S.). 三、实践应用 例 1 如图,∠ABC=∠DCB,∠ABD=∠DCA,试说明:AB=DC. 3 解 因为∠ABC=∠DCB,∠ABD=∠DCA, 所以∠ABC-∠ABD=∠DCB-∠DCA, 即∠DBC=∠ACB, 在中,∠ABC=∠DCB,BC=CB(公共边),∠ACB=∠DBC, 所以由(A.S.A)全等识别法,可知 △ABC≌△DCB 所以 AB=DC(全等三角形的对应边相等). 例 2 已知,如图,△ABC≌△A′B′C′,AD、A′D′分别是△ABC 和△A′B′C′的高,试 说明:AD=A′D′. 分析 已知△ABC≌△A′B′C′,相当于已知它们的对应边相等,对应角相等.在证明过程 中,可根据需要,选取其中的一部分相等关系. 解 因为△ABC≌△A′B′C′, 所以 AB=A′B′,∠B=∠B′ (全等三角形的对应边、对应角相等), 因为 AD、A′D′分别是△ABC 和△A′B′C′的高, 所以∠ADB=∠A′D′B′=90°. 在△ABD 和△A′B′D′中,∠B=∠B′,∠ADB=∠A′D′B′,AB=A′B′, 所以由(A.A.S.)全等识别法,可知 △ABD≌△A′B′D′. 所以 AD=A′D′ (全等三角形的对应边相等). 四、交流反思 本节课我们主要学习了什么内容?请一位同学来小结一下. 1.学习了“已知两角及一边画三角形”的方法. 2.全等识别法:如果两个三角形有两个角及其夹边分别对应相等,那么这两个三角形全 等.(A.S.A.) 3.全等识别法:如果两个三角形有两个角和其中一角的对边分别对应相等,那么这两个三角 形全等.(A.A.S. ) 五、检测反馈 练习 1.根据题目条件,判别下面的两个三角形是否全等,并说明理由. 4 2.△ABC 是等腰三角形,AD、BE 分别是∠A、∠B 的角平分线,△ABD 和△BAE 全等吗?试说 明理由. 3.要测量河两岸相对的两点 A 和 B 的距离,可以在 AB 的垂线 BF 上取两点 C、D,使 CD=BC, 再作 BF 的垂线 DE,使 A、C、E 三点在同一直线上,这时,测得 DE 的长就是 AB 的距离.试 用全等三角形的知识说明其中的道理. 六、板书设计 (课题) 复习: 结论: 思考: 例 2. A.A.S 问题: 证明: (学生板演)查看更多