2019秋八年级数学上册第11章数的开方小结与复习课件

2019秋八年级数学上册第11章数的开方小结与复习课件

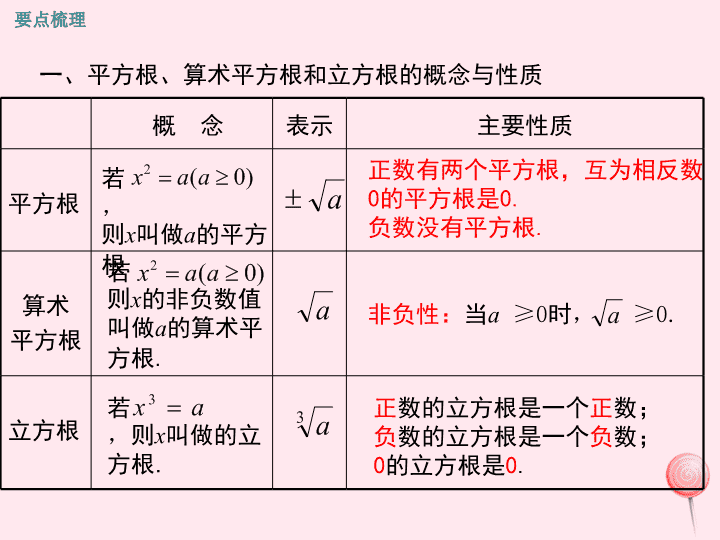
小结与复习 第11章 数的开方 要点梳理 考点讲练 课堂小结 课后作业 一、平方根、算术平方根和立方根的概念与性质 概 念 表示 主要性质 平方根 算术 平方根 立方根 若 ， 则x叫做a的平方 根. 2 ( 0)x a a  a 正数有两个平方根，互为相反数 0的平方根是0. 负数没有平方根. 若 则x的非负数值 叫做a的算术平 方根. 2 ( 0)x a a  a 非负性：当a ≥0时， ≥0.a 若 ，则x 叫做的立方根. 3x a 3 a 正数的立方根是一个正数； 负数的立方根是一个负数； 0的立方根是0. 要点梳理 联 系 平方根与算术平方根：(1)具有包含关系：平方 根包含算术平方根，算术平方根是平方根中的一种； (2)存在条件相同：平方根和算术平方根都只有　　 才有；(3)0的平方根、算术平方根均为　 　. 平方根与立方根：(1)都与相应的乘方运算互为　 　运算；(2)都可归结为非负数的非负方根来研 究．平方根主要通过算术平方根来研究，而负数的立 方根也可通过转化为正数的立方根来研究，即 ＝　　 ； (3)0的平方根和立方根都是0.　 非负数 0 逆 － 3 a 3 a 二、开平方与开立方 求一个非负数a的　 　的运算，叫做开平方．其 中a叫做　 　. 求一个数a的　 　的运算，叫做开立方．其中a 叫做　 　. 开平方与　 　、开立方与　 　都分别互为逆 运算． [点拨] (1)求正数的平方根时，往往先求出其算术 平方根，再在求出的数前面加上“±”号；(2)根据平 方(立方)运算与开平方(开立方)运算互为逆运算的关 系，我们可以通过平方(立方)运算来求一个数的平方 根(立方根)． 平方根 被开方数 立方根 被开方数 平方 立方 强调：数的开方的几个重要性质 性质1： a ≥0 (a≥0) （双重非负性） 性质2： ( a )2 = a (a≥0) 性质3： （a≥0） a （a＜0）-a a2 = |a| = 性质4： 3 3a a   [点拨]算术平方根的双重非负性：算术平方根的符号“ ” 不仅是一个运算符号(对被开方数实施开平方运算)，另一方面 也是一个性质符号，即表示非负数a的正的平方根． 1. 用计算器求一个正数的算术平方根 三、用计算器求算术平方根、立方根 2. 用计算器求立方根 用计算器求一个数a的立方根，只需要按书写顺序在 计算器上依次键入 （ ） SHIFT a = a = 用计算器求一个正数a的算术平方根，只需要按书写 顺序在计算器上依次键入 3 四、实数 1.实数的分类 (1)按定义分： (2)按符号分： 实 数 有 理 数 分数 整数 无 理 数 （有限小数及 无限循环小数） （无限不循环小数） 实 数 正实数 负实数 正有理数 正无理数 负有理数 负无理数 0 2.实数与数轴 (1)实数和数轴上的点是一一对应的关系； (2)在数轴上表示的两个数，右边的数总比左边的数大. 3.在实数范围内，有理数的有关概念、大小比较法则、运 算法则以及运算律同样适用. 考点讲练 考点一 平方根、算术平方根及立方根 例1 已知一个正数的两个平方根分别是a+3和2a-18， 求这个正数. 【解析】根据一个正数的平方根有两个，它们互为相反 数，可以得到关于a的一元一次方程，解之求得a的值， 从而可求出这个正数. 解：根据平方根的性质，有a+3+2a-18=0，解得a=5， a+3=8，82=64，所以这个正数是64. 一个正数的平方根有两个，它们互为相反数．而一 个非负数的算术平方根只有一个.另外，一个数的立方 根也只有一个，且与它本身的符号相同. 方法总结 1.下列说法正确的有（ ） -64的立方根是-4； 49的算术平方根是±7；  的立方根是 ； ④ 的平方根是 . A.1个 B.2个 C.3 个 D.4个 1 27 1 3 1 16 1 4 B 针对训练 C2. 的平方根是 （ ） A.4 B.2 C.±2 D.±4 16 例2 若a，b为实数且 +|b-1|=0，则(ab)2016 = . 1a  3.若 与(b-27)2 互为相反数，则 .3 3a b 8a  -11 【解析】先根据非负数的性质求出a，b的值，再根据乘 方的定义求出(ab)2016的值.∵ +|b-1|=0，∴a+1=0，且 b-1 =0，∴a =-1 ，b =1.∴(ab)2016 = (-1×1)2016= (-1)2016=1 ， 故填1. 1a  1 初中阶段主要涉及三种非负数： ≥0，|a|≥0，a2≥0.如 果若干个非负数的和为0，那么这若干个非负数都必为0. a 方法总结 针对训练 4 .在实数 π， ，0，-1 中，无理数是（ ） A.π B. C.0 D.-1 1 5 1 5 B例3 在实数 ， ， 中，无理数有 （ ） A.3个 B.2个 C.1个 D.0个 3 4 2 π2 2 A 考点二 无理数的识别 针对训练 【解析】 是分数； 虽然含有分母2，但它的分子是无理 数 ，所以 是无理数；同理 也是无理数. 故选B. 3 4 2 2 2 2 π2 2 例4 如图，数轴上的点A，B分别对应 实数a，b，下列结论正确的是（ ） A.a>b B.|a|>|b| C.-a0，根据|a|<|b|，知-a

查看更多