- 2021-10-26 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
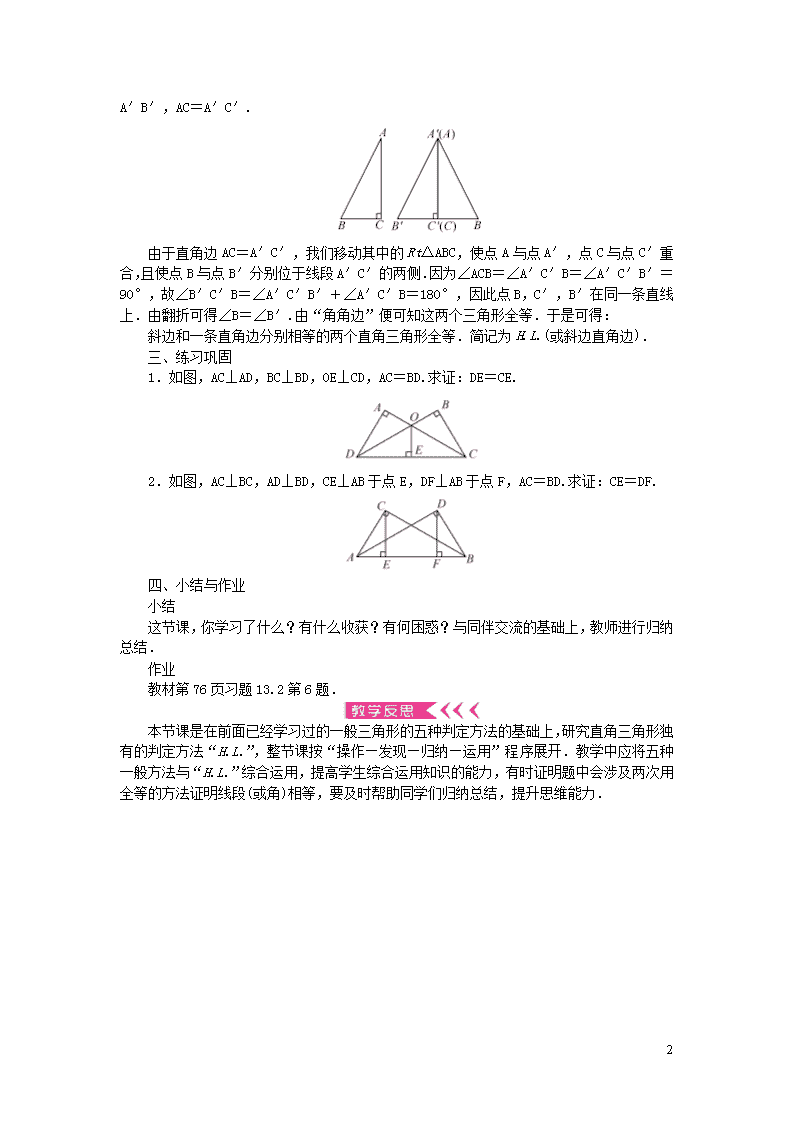
八年级数学上册第13章全等三角形13-2三角形全等的判定13.2.6 斜边直角边
13.2.6 斜边直角边 1.会用“H.L.”判定两个直角三角形全等. 2.会综合应用各种方法判定两个直角三角形全等. 重点 用“H.L.”判定两个直角三角形全等. 难点 用综合法证明两个直角三角形全等. 一、创设情境 问题:舞台背景的形状是两个直角三角形,工作人员想知道这两个直角三角形是否全等,但每个三角形都有一条直角边被花盆遮住无法测量. (1)你能帮他想个办法吗? (2)如果他只带了一个卷尺,能完成这个任务吗? 问题(1)学生可以回答去量斜边和一锐角,或直角边和一个锐角;但对于问题(2),学生则难肯定.工作人员测量了每个三角形没有被遮住的直角边和斜边,发现它们分别对应相等,于是他就肯定“两个直角三角形是全等的”,你相信他的结论吗? 二、探究新知 我们已经知道,对于两个三角形,如果有“边角边”或“角边角”或“角角边”或“边边边”分别对应相等,那么这两个三角形一定全等;如果有“角角角”分别对应相等,那么不能判定这两个三角形全等,这两个三角形可以有不同的大小;如果有“边边角”分别对应相等,也不能保证这两个三角形全等. 那么在两个直角三角形中,当斜边和一条直角边分别对应相等时,也具有“边边角”对应相等的条件,这时这两个直角三角形能否全等吗? 如图,已知两条线段(这两条线段长不相等),以长的线段为斜边、短的线段为一条直角边,画一个直角三角形. 把你画的直角三角形与其他同学画的直角三角形进行比较,所有的直角三角形都全等吗? 换两条线段,试试看,是否有同样的结论? 步骤: 1.画一线段AB,使它等于2 cm; 2.画∠MAB=90°; 3.以点B为圆心,以3 cm长为半径画圆弧,交射线AM于点C; 4.连结BC. △ABC即为所求. 如图,在Rt△ABC和Rt△A′B′C′中,已知∠ACB=∠A′C′B′=90°,AB 2 =A′B′,AC=A′C′. 由于直角边AC=A′C′,我们移动其中的Rt△ABC,使点A与点A′,点C与点C′重合,且使点B与点B′分别位于线段A′C′的两侧.因为∠ACB=∠A′C′B=∠A′C′B′=90°,故∠B′C′B=∠A′C′B′+∠A′C′B=180°,因此点B,C′,B′在同一条直线上.由翻折可得∠B=∠B′.由“角角边”便可知这两个三角形全等.于是可得: 斜边和一条直角边分别相等的两个直角三角形全等.简记为H.L.(或斜边直角边). 三、练习巩固 1.如图,AC⊥AD,BC⊥BD,OE⊥CD,AC=BD.求证:DE=CE. 2.如图,AC⊥BC,AD⊥BD,CE⊥AB于点E,DF⊥AB于点F,AC=BD.求证:CE=DF. 四、小结与作业 小结 这节课,你学习了什么?有什么收获?有何困惑?与同伴交流的基础上,教师进行归纳总结. 作业 教材第76页习题13.2第6题. 本节课是在前面已经学习过的一般三角形的五种判定方法的基础上,研究直角三角形独有的判定方法“H.L.”,整节课按“操作—发现—归纳—运用”程序展开.教学中应将五种一般方法与“H.L.”综合运用,提高学生综合运用知识的能力,有时证明题中会涉及两次用全等的方法证明线段(或角)相等,要及时帮助同学们归纳总结,提升思维能力. 2查看更多