2020八年级数学上册 第十二章 全等三角形检测题 （新版）新人教版

2020八年级数学上册 第十二章 全等三角形检测题 （新版）新人教版

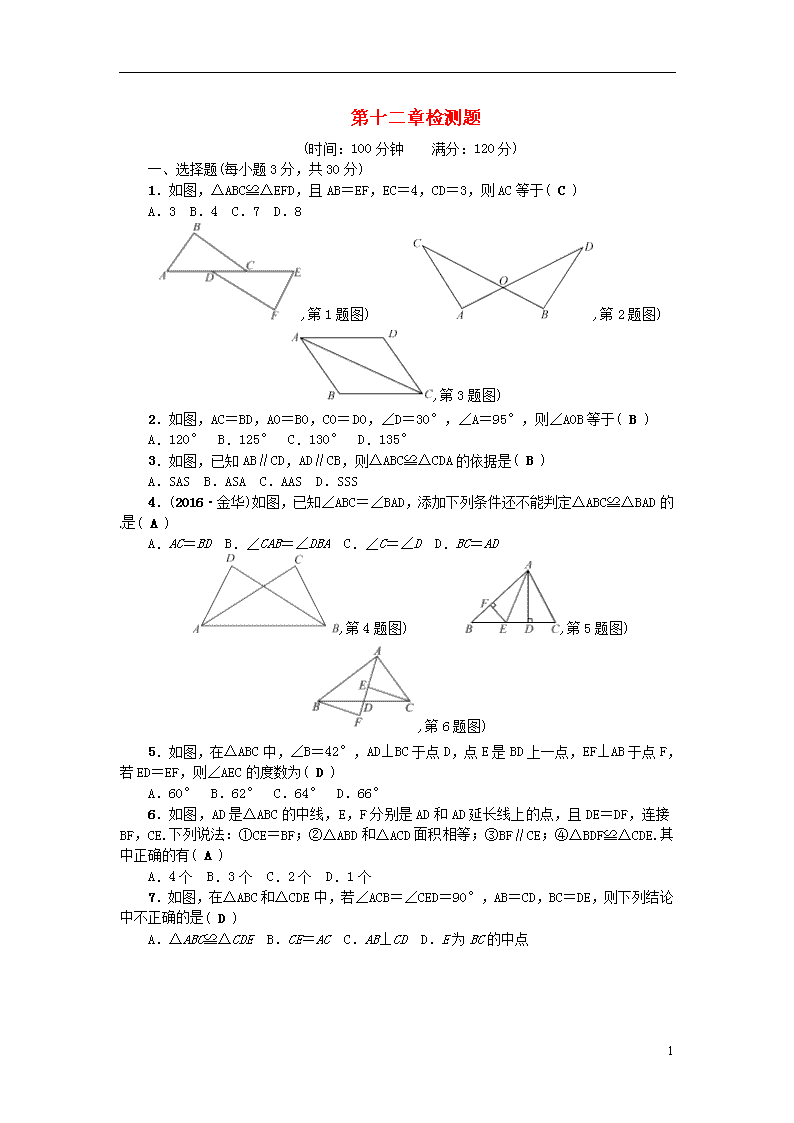
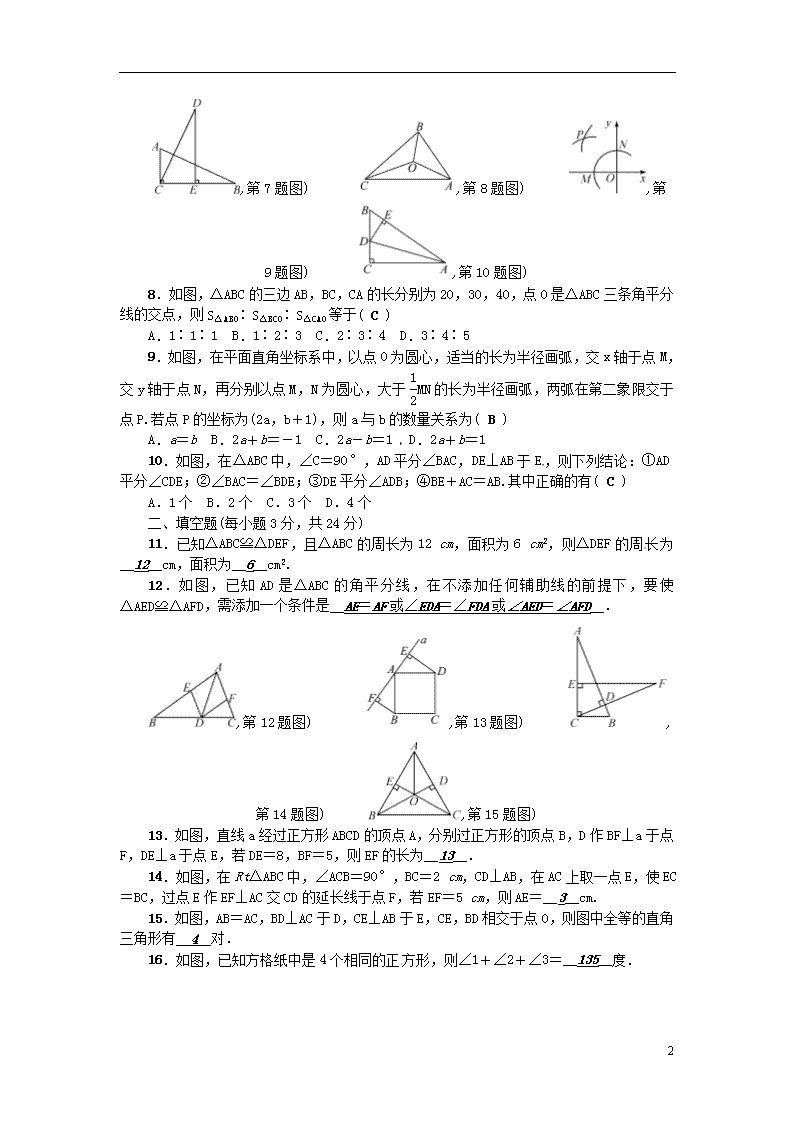
第十二章检测题 ‎(时间：100分钟　　满分：120分)‎ 一、选择题(每小题3分，共30分)‎ ‎1．如图，△ABC≌△EFD，且AB＝EF，EC＝4，CD＝3，则AC等于( C )‎ A．3 B．‎4 C．7 D．8‎ ‎,第1题图)　　　,第2题图)　　　,第3题图)‎ ‎2．如图，AC＝BD，AO＝BO，CO＝DO，∠D＝30°，∠A＝95°，则∠AOB等于( B )‎ A．120° B．125° C．130° D．135°‎ ‎3．如图，已知AB∥CD，AD∥CB，则△ABC≌△CDA的依据是( B )‎ A．SAS B．ASA C．AAS D．SSS ‎4．(2016·金华)如图，已知∠ABC＝∠BAD，添加下列条件还不能判定△ABC≌△BAD的是( A )‎ A．AC＝BD B．∠CAB＝∠DBA C．∠C＝∠D D．BC＝AD ‎,第4题图)　　　　,第5题图)　　　　,第6题图)‎ ‎5．如图，在△ABC中，∠B＝42°，AD⊥BC于点D，点E是BD上一点，EF⊥AB于点F，若ED＝EF，则∠AEC的度数为( D )‎ A．60° B．62° C．64° D．66°‎ ‎6．如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE＝DF，连接BF，CE.下列说法：①CE＝BF；②△ABD和△ACD面积相等；③BF∥CE；④△BDF≌△CDE.其中正确的有( A )‎ A．4个 B．3个 C．2个 D．1个 ‎7．如图，在△ABC和△CDE中，若∠ACB＝∠CED＝90°，AB＝CD，BC＝DE，则下列结论中不正确的是( D )‎ A．△ABC≌△CDE B．CE＝AC C．AB⊥CD D．E为BC的中点 6‎ ‎,第7题图)　　　,第8题图)　　　,第9题图)　　　,第10题图)‎ ‎8．如图，△ABC的三边AB，BC，CA的长分别为20，30，40，点O是△ABC三条角平分线的交点，则S△ABO∶S△BCO∶S△CAO等于( C )‎ A．1∶1∶1 B．1∶2∶‎3 C．2∶3∶4 D．3∶4∶5‎ ‎9．如图，在平面直角坐标系中，以点O为圆心，适当的长为半径画弧，交x轴于点M，交y轴于点N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧在第二象限交于点P.若点P的坐标为(‎2a，b＋1)，则a与b的数量关系为( B )‎ A．a＝b B．‎2a＋b＝－‎1 C．‎2a－b＝1 D．‎2a＋b＝1‎ ‎10．如图，在△ABC中，∠C＝90°，AD平分∠BAC，DE⊥AB于E，则下列结论：①AD平分∠CDE；②∠BAC＝∠BDE；③DE平分∠ADB；④BE＋AC＝AB.其中正确的有( C )‎ A．1个 B．2个 C．3个 D．4个 二、填空题(每小题3分，共24分)‎ ‎11．已知△ABC≌△DEF，且△ABC的周长为‎12 cm，面积为‎6 cm2，则△DEF的周长为__12__cm，面积为__6__cm2.‎ ‎12．如图，已知AD是△ABC的角平分线，在不添加任何辅助线的前提下，要使△AED≌△AFD，需添加一个条件是__AE＝AF或∠EDA＝∠FDA或∠AED＝∠AFD__．‎ ‎,第12题图)　　　,第13题图)　　　,第14题图)　　　,第15题图)‎ ‎13．如图，直线a经过正方形ABCD的顶点A，分别过正方形的顶点B，D作BF⊥a于点F，DE⊥a于点E，若DE＝8，BF＝5，则EF的长为__13__．‎ ‎14．如图，在Rt△ABC中，∠ACB＝90°，BC＝‎2 cm，CD⊥AB，在AC上取一点E，使EC＝BC，过点E作EF⊥AC交CD的延长线于点F，若EF＝‎5 cm，则AE＝__3__cm.‎ ‎15．如图，AB＝AC，BD⊥AC于D，CE⊥AB于E，CE，BD相交于点O，则图中全等的直角三角形有__4__对．‎ ‎16．如图，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3＝__135__度．‎ 6‎ ‎,第16题图)　　　　,第17题图)　　　　,第18题图)‎ ‎17．如图，已知相交直线AB和CD及另一直线MN，如果要在MN上找出与AB，CD距离相等的点，则这样的点至少有__1__个，最多有__2__个．‎ ‎18．如图，已知△ABC的三个内角的平分线交于点O，点D在CA的延长线上，且DC＝BC，若∠BAC＝80°，则∠BOD的度数为__100°__．‎ 三、解答题(共66分)‎ ‎19．(7分)(2016·十堰)如图，AB∥CD，E是CD上一点，BE交AD于点F，EF＝BF.求证：AF＝DF.‎ 解：∵AB∥CD，∴∠B＝∠FED.在△ABF和△DEF中，‎ ∴△ABF≌△DEF，∴AF＝DF ‎20．(8分)如图，工人师傅要检查人字梁的∠B和∠C是否相等，但他手边没有量角器，只有一个刻度尺．他是这样操作的：①分别在BA和CA上取BE＝CG；②在BC上取BD＝CF；③量出DE的长为a m，FG的长为b m．如果a＝b，则说明∠B和∠C是相等的，他的这种做法合理吗？为什么？‎ 解：合理，理由：如果a＝b，由SSS可证△BED≌△CGF，∴∠B＝∠C 6‎ ‎21．(8分)如图，在△ABC中，∠C＝90°，AD平分∠CAB，DE⊥AB于点E，点F在AC上，BE＝FC，求证：BD＝DF.‎ 解：由角的平分线的性质可得CD＝DE，再由SAS证△CDF≌△EDB，可得BD＝DF ‎22．(8分)如图，AB＝AC，BD＝CD，DE⊥AB于点E，DF⊥AC于点F.求证：DE＝DF.‎ 解：连接AD，在△ACD和△ABD中，∴△ACD≌△ABD(SSS)，∴∠EAD＝∠FAD，即AD平分∠EAF.∵DE⊥AE，DF⊥AF，∴DE＝DF ‎23．(10分)如图①，点A，E，F，C在同一直线上，AE＝CF，过点E，F分别作ED⊥AC 6‎ ‎，FB⊥AC，AB＝CD.‎ ‎(1)若BD与EF交于点G，试证明BD平分EF；‎ ‎(2)若将△DEC沿AC方向移动到图②的位置，其他条件不变，上述结论是否仍然成立？请说明理由．‎ 解：(1)先由HL证Rt△ABF≌Rt△CDE，∴BF＝DE，再由AAS证△GFB≌△GED，∴EG＝FG，即BD平分EF　(2)仍然成立，证法同(1)‎ ‎24．(12分)如图，在△ABC中，∠B＝∠C，AB＝‎10 cm，BC＝‎8 cm，D为AB的中点，点P在线段上以‎3 cm/s的速度由点B向点C运动，同时，点Q在线段CA上以相同速度由点C向点A运动，一个点到达终点后另一个点也停止运动．当△BPD与△CQP全等时，求点P运动的时间．‎ 解：∵D为AB的中点，AB＝10 cm，∴BD＝AD＝5 cm.设点P运动的时间是x s，若BD与CQ是对应边，则BD＝CQ，∴5＝3x，解得x＝，此时BP＝3×＝5 (cm)，CP＝8－5＝3 (cm)，BP≠CP，故舍去；若BD与CP是对应边，则BD＝CP，∴5＝8－3x，解得x＝1，符合题意．综上可知，点P运动的时间是1 s ‎25．(13分)如图，在△ABC和△ADE中，AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°.‎ ‎(1)当点D在AC上时，如图①，线段BD，CE有怎样的数量关系和位置关系？请证明你的猜想；‎ ‎(2)将图①中的△ADE绕点A顺时针旋转α(0°＜α＜90°)，如图②，线段BD，CE有怎样的数量关系和位置关系？请说明理由．‎ 6‎ 解：(1)BD＝CE，BD⊥CE.证明：延长BD交CE于M，易证△ABD≌△ACE(SAS)，∴BD＝CE，∠ABD＝∠ACE，∵∠BME＝∠MBC＋∠BCM＝∠MBC＋∠ACE＋∠ACB＝∠MBC＋∠ABD＋∠ACB＝∠ABC＋∠ACB＝90°，∴BD⊥CE　(2)仍有BD＝CE，BD⊥CE，理由同(1)‎ 6‎