八年级下册数学同步练习17-1 第3课时 利用勾股定理作图或计算 人教版

八年级下册数学同步练习17-1 第3课时 利用勾股定理作图或计算 人教版

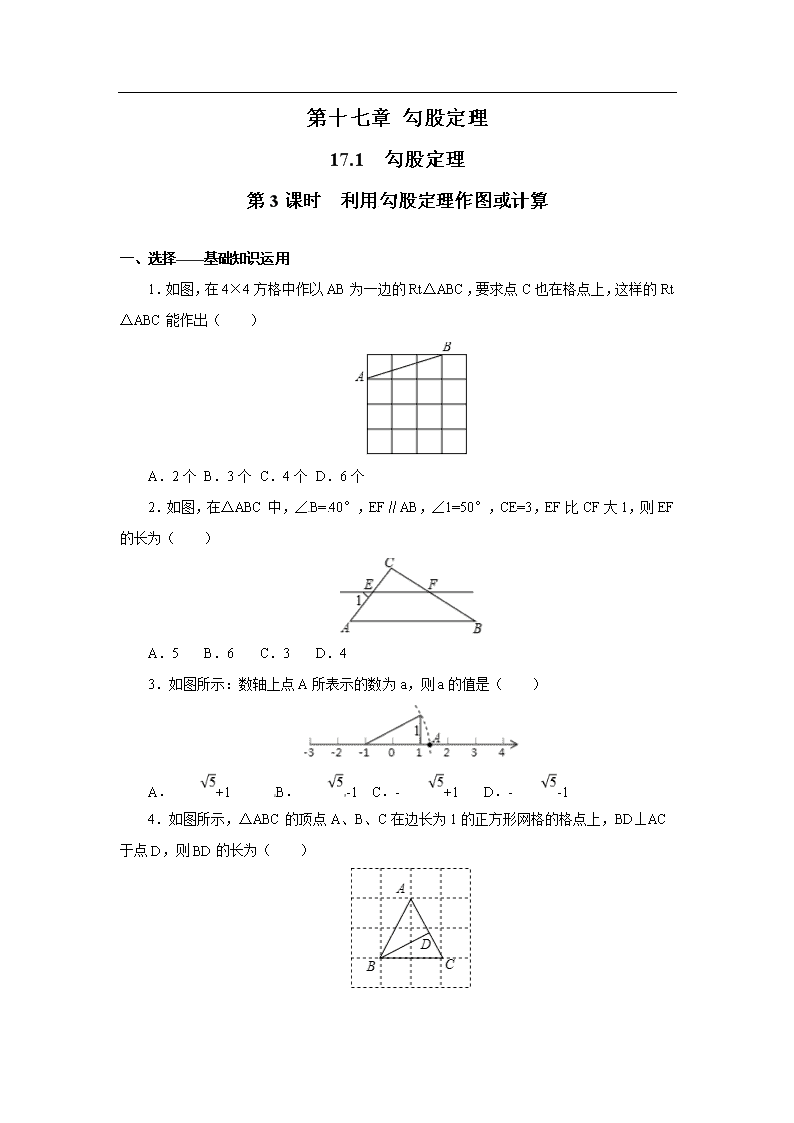
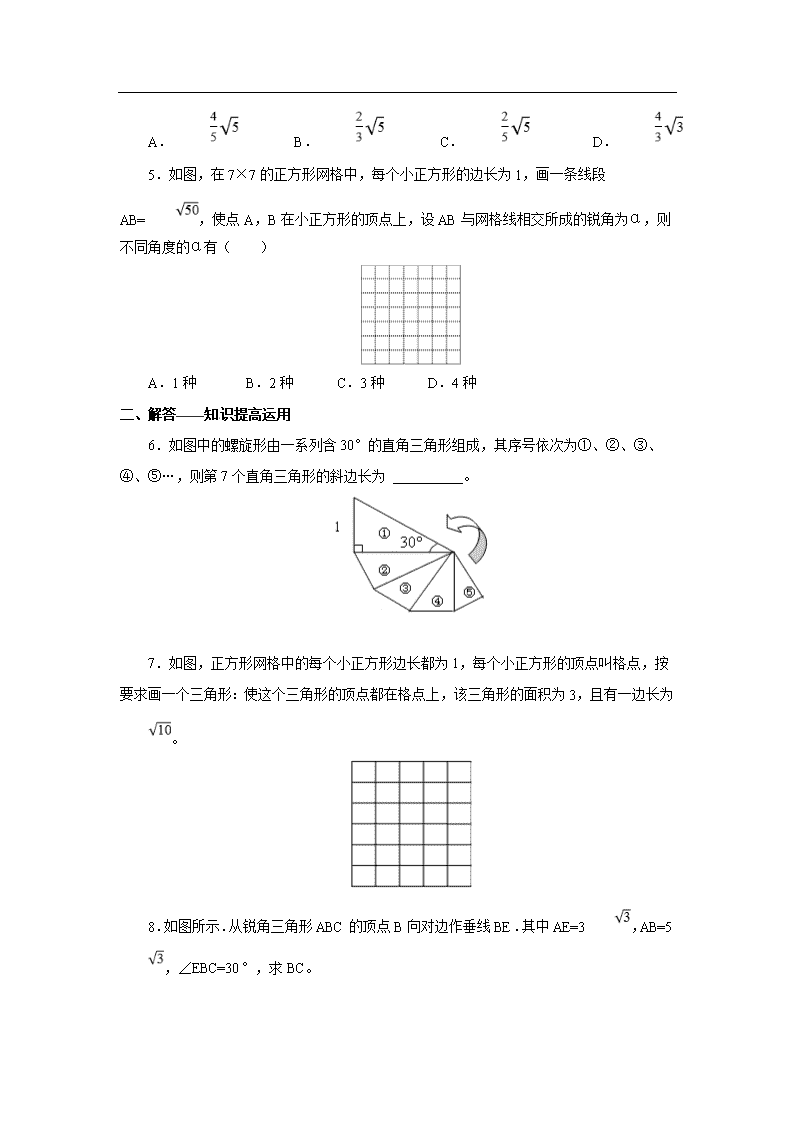
第十七章 勾股定理 ‎17.1 勾股定理 第3课时 利用勾股定理作图或计算 一、选择——基础知识运用 ‎1．如图，在4×4方格中作以AB为一边的Rt△ABC，要求点C也在格点上，这样的Rt△ABC能作出（　　）‎ A．2个 B．3个 C．4个 D．6个 ‎2．如图，在△ABC中，∠B=40°，EF∥AB，∠1=50°，CE=3，EF比CF大1，则EF的长为（　　）‎ A．5 B．6 C．3 D．4‎ ‎3．如图所示：数轴上点A所表示的数为a，则a的值是（　　）‎ A．+1 B．-1 C．-+1 D．--1‎ ‎4．如图所示，△ABC的顶点A、B、C在边长为1的正方形网格的格点上，BD⊥AC于点D，则BD的长为（　　）‎ A． B． C． D．‎ ‎5．如图，在7×7的正方形网格中，每个小正方形的边长为1，画一条线段AB=，使点A，B在小正方形的顶点上，设AB与网格线相交所成的锐角为α，则不同角度的α有（　　）‎ A．1种 B．2种 C．3种 D．4种 二、解答——知识提高运用 ‎6．如图中的螺旋形由一系列含30°的直角三角形组成，其序号依次为①、②、③、④、⑤…，则第7个直角三角形的斜边长为 。‎ ‎7．如图，正方形网格中的每个小正方形边长都为1，每个小正方形的顶点叫格点，按要求画一个三角形：使这个三角形的顶点都在格点上，该三角形的面积为3，且有一边长为。‎ ‎8．如图所示．从锐角三角形ABC的顶点B向对边作垂线BE．其中AE=3，AB=5，∠EBC=30°，求BC。‎ ‎9．如图，在一张长方形ABCD纸张中，一边BC折叠后落在对角线BD上，点E为折痕与边CD的交点，若AB=5，BC=12，求图中阴影部分的面积。‎ ‎10．在平面直角坐标系内，已知点A（2，2）．B（2，3），点P在y轴上，且三角形APB为直角三角形，求点P的坐标。‎ ‎11．（1）在右面的方格纸中，以线段AB为一边，画一个正方形；‎ ‎（2）如果图中小方格的面积为1平方厘米，你知道（1）中画出的正方形的面积是多大吗？解释你的计算方法。‎ 参考答案 一、选择——基础知识运用 ‎1．【答案】D ‎【解析】‎ 当AB是斜边时，则第三个顶点所在的位置有：C、D，E，H四个；‎ 当AB是直角边，A是直角顶点时，第三个顶点是F点；‎ 当AB是直角边，B是直角顶点时，第三个顶点是G．[来源:学科网ZXXK]‎ 因而共有6个满足条件的顶点．‎ 故选D。‎ ‎2．【答案】A ‎【解析】∵EF∥AB，‎ ‎∴∠A=∠1=50°，‎ ‎∴∠A+∠B=50°+40°=90°，‎ ‎∴∠C=90°，‎ 设CF=x，则EF=x+1，‎ 根据勾股定理得：CE2+CF2=EF2，‎ 即32+x2=（x+1）2，‎ 解得：x=4，[来源:学科网ZXXK]‎ ‎∴EF=4+1=5，‎ 故选：A。‎ ‎3．【答案】B ‎4．【答案】A ‎【解析】‎ ‎△ABC的面积=×BC×AE=2，‎ 由勾股定理得，AC==，‎ 则××BD=2，‎ 解得BD=。故选：A。‎ ‎5．【答案】C ‎【解析】解如图所示：‎ ‎∵==5=AB，此时AB与网格线相交所成的锐角α=45°；‎ ‎==5=AB，此时AB与网格线相交所成的锐角α有两个不同的角度；[来源:学|科|网Z|X|X|K]‎ ‎∴AB与网格线相交所成的锐角α，不同角度的α有3个；‎ 故选：C。‎ 二、解答——知识提高运用 ‎6．【答案】‎ ‎【解析】‎ 设第二个直角三角形的斜边长是x ‎∵tan30°= ，‎ ‎∴x==1×，‎ 同理第3个直角三角形斜边长是 =×，‎ 第4个直角三角形的斜边长是：××=，‎ 第7个直角三角形斜边的长是××=‎ 故答案为：。‎ ‎7．【答案】面积为3，我们不妨取底边为2，高为3的一个三角形；又该三角形有一边长为，则可以看作是两直角边分别为3，1的直角三角形的斜边，由此我们可以在网格上画出这个图形。‎ ‎8．【答案】在直角△AEB中，AE=3，AB=5，‎ 则BE==4，‎ ‎∵∠BEC=90°，∠EBC=30°，‎ ‎∴BC=2CE（直角三角形中30°角所对直角边为斜边长的一半），‎ ‎∵BC2=CE2+BE2，‎ ‎∴3CE2=BE2=48，[来源:Zxxk.Com]‎ ‎∴CE=4，BC=8．‎ 答：BC的长为 8。‎ ‎9．【答案】因为BC折叠后落在对角线BD上，设C的对应点是F，则EF⊥BD，‎ ‎△DEF是直角三角形，∠DFE=90°‎ 因为BD是长方形ABCD的对角线，‎ 所以BD=＝13，‎ DF=13-12=1，‎ 设CE=x，则EF=CE=x，DE=5-x，‎ 在△DEF中，x2+12=（5-x）2，‎ 解得x＝，‎ 所以图中阴影部分的面积S△BDE＝×13×＝。‎ ‎10．【答案】画出平面直角坐标系，‎ AB为直角边，（1）∠ABP为直角，P1A2=P1B2+AB2，则P1的坐标（0，3），‎ ‎（2）∠BAP为直角，P2B2=AB2+P2A2，则P2的坐标（0，2）。[来源:学科网]‎ 故点P的坐标为（0，2），（0，3）。‎ ‎11．【答案】（1）过AB分别作ADABBCAB，并且使得AD=BC=AB，连接CD，‎ 则正方形ABCD为题目要求的正方形．‎ ‎（2）图中小方格为1cm，‎ 则AB==，‎ 故正方形ABCD的面积S=AB2=53。‎ 答：正方形面积为53。‎