八年级下数学课件《一元二次方程（2）》课件_鲁教版

八年级下数学课件《一元二次方程（2）》课件_鲁教版

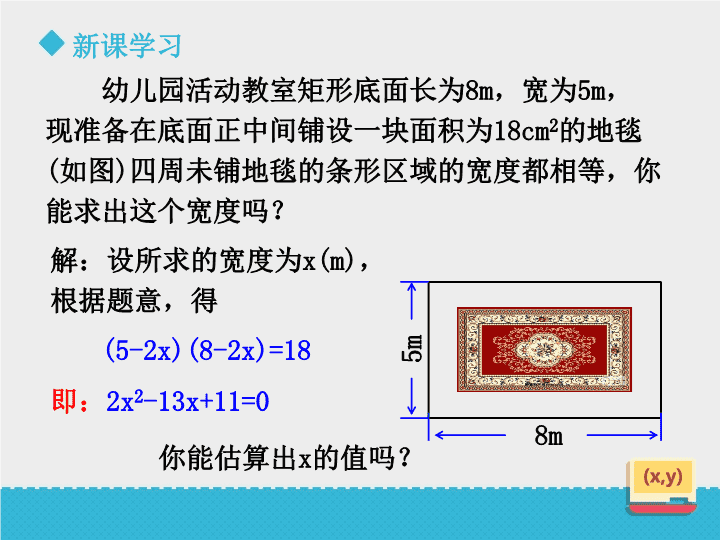
鲁教版初中数学八年级下册第八单元第2课 导入新课在上一节课中，我们得到了如下的两个一元二次方程：(5-2x)(8-2x)=18，即：2x2-13x+11=0；(x+6)2+72=102，即：x2+12x-15=0.你能求出各方程中的x吗？ 幼儿园活动教室矩形底面长为8m，宽为5m，现准备在底面正中间铺设一块面积为18cm2的地毯(如图)四周未铺地毯的条形区域的宽度都相等，你能求出这个宽度吗？8m5m(5-2x)(8-2x)=18即：2x2-13x+11=0新课学习解：设所求的宽度为x(m)，根据题意，得你能估算出x的值吗？ 新课学习（1）根据题目的已知条件，你能确定x的大致范围吗？说说你的理由．0＜x＜2.5因为，教室矩形底面的宽为5m，所以四周未铺地毯的条形区域的宽度不能超过2.5m. x不可能小于0：x表示的是地毯的宽度.x不可能大于4，也不可能大于2.5：当x大于4和当x大于2.5时，将分别使原矩形地面的长和宽小于0，不符合实际情况.（2）x可能小于0吗？x可能大于4吗？可能大于2.5吗？说说你的理由，并与同伴进行交流．新课学习 新课学习（4）你知道所求的宽度x(m)是多少吗?还有其他求解方法吗?与同伴进行交流．（3）完成下表：x00.511.522.52x2-13x+11-91150-4-7 新课学习当x=1时，代数式2x2-13x+11的值等于0；所以，花边的宽度为1m。如果把(8-2x)(5-2x)=18看做6×3=18，则有：8-2x=6，5-2x=3.从而也可解得x=1. 新课学习用“夹逼”思想解一元二次方程的步骤：①在未知数x的取值范围内排除一部分取值；②根据题意所列的具体情况再次进行排除；③列出能反映未知数和方程的值的表格进行再次筛选；④最终得出未知数的最小取值范围或具体数据。 新课学习如图，一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m．如果梯子的顶端下滑1m，那么梯子的底端滑动多少米？解：设梯子底端向外滑动xm，根据题意，得：(x+6)2+72=102即：x2+12x-15=0做一做 新课学习(1)小明认为底端也滑动了1m，他的说法正确吗？为什么？不正确.根据勾股定理可知：若底端也滑动了1m，则72+(6+1)2＜10210 (2)底端滑动的距离可能是2m吗？可能是3m吗？为什么？不可能是2m，也不可能是3m.根据勾股定理可知：若底端滑动了2m，则72+(6+2)2＞102新课学习 新课学习(3)你能猜出滑动距离x(m)的大致范围吗？小亮把他的求解过程整理如下：x00.511.52x2+12x-15-15-8.75-25.2513所以1＜x＜1.5当x的取值是1和2时，所对应的代数式的值是-2和13，而且随着x取值的增大，相应代数式的值越大，因此要想使代数式的值为0，那么x的取值应在1和1.5之间 新课学习进一步计算：x1.11.21.31.4x2+12x-15-0.590.842.293.76所以1.1＜x＜1.2因此x的整数部分是1，十分位是1.(4)x的整数部分是几？十分位是几？当x的取1.1到1.4的值时，所对应的代数式的值在-0.59和3.76之间，而且随着x取值的增大，相应代数式的值越大，因此要想使代数式的值为0，那么x的取值应在1.1和1.2之间. 结论总结谈谈你这节课的收获？通过本节课的学习了解了估算一元二次方程ax２+bx+c=０(a，b，c为常数，a≠０)近似解的方法，知道了估算的步骤是先确定大致范围，再取值计算，逐步逼近. x1.11.21.31.42x2-x-2=0-0.68-0.320.080.521、根据下列表格的对应值：判断方程2x2-x-2=0的一个解x的范围是()A.1.1＜x＜1.2C.1＜x＜1.3D.1.2＜x＜1.3B.1.1＜x＜1.4课堂练习D 课堂练习x3.233.243.253.26ax2+bx+c=0-0.06-0.020.030.07A.3＜x＜3.23C.3.24＜x＜3.25D.3.25＜x＜3.26B.3.23＜x＜3.24C2、根据下表的对应值，试判断一元二次方程ax2+bx+c=0(a≠0，a、b、c为常数)的解的范围是() 课堂练习3、五个连续整数，前三个数的平方和等于后两个数的平方.你能估算出这五个整数分别是多少吗？解：设五个连续整数中的第一个数为x，那么后面四个数依次可表示为x+1,x+2,x+3,x+4.根据题意，可得方程：x2+(x+1)2+(x+2)2=(x+3)2+(x+4)2即：x2-8x-20=0方法一： 课堂练习x-3-2…910x2-8x-20130…-110方程：x2-8x-20=0所以，x=-2或x=10所以5个连续的整数为：-2,-1,0,1,2或10,11,12,13,14 课堂练习解：设五个连续整数中的中间一个数为x，那么其余四个数依次可表示为x-2,x1,x+1,x+2.根据题意，可得方程：(x-2)2+(x-1)2+x2=(x+1)2+(x+2)2即：x2-12x=0方法二：x-10…1112x2-12x130…-110所以，x=0或x=12所以5个连续的整数为：-2,-1,0,1,2或10,11,12,13,14 板书设计估算求一元二次方程的近似解(1)将方程化为一元二次方程的一般形式；(2)根据实际情况确定其解的大致范围；(3)在这一范围内均匀的取一些x的值，将这些值分别代入方程中，哪两个值最接近0，方程的解就在这两个值对应的两个x值之间. 作业布置P54页：习题8.2