八年级下数学课件《三角形的中位线》 (11)_苏科版

八年级下数学课件《三角形的中位线》 (11)_苏科版

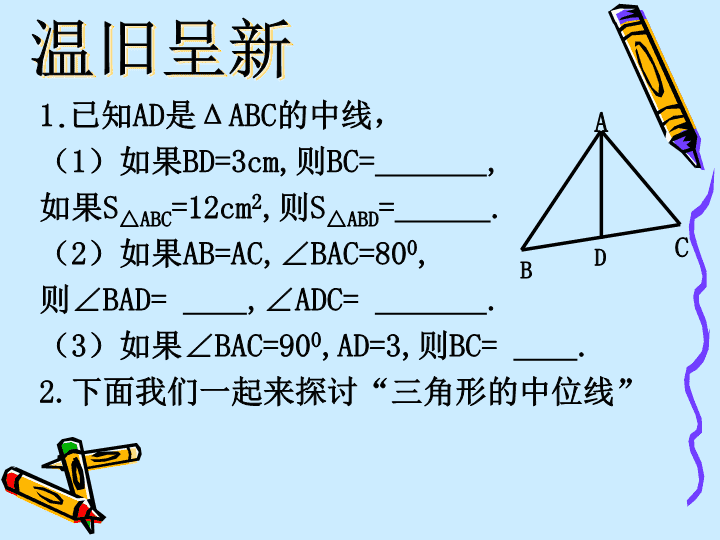
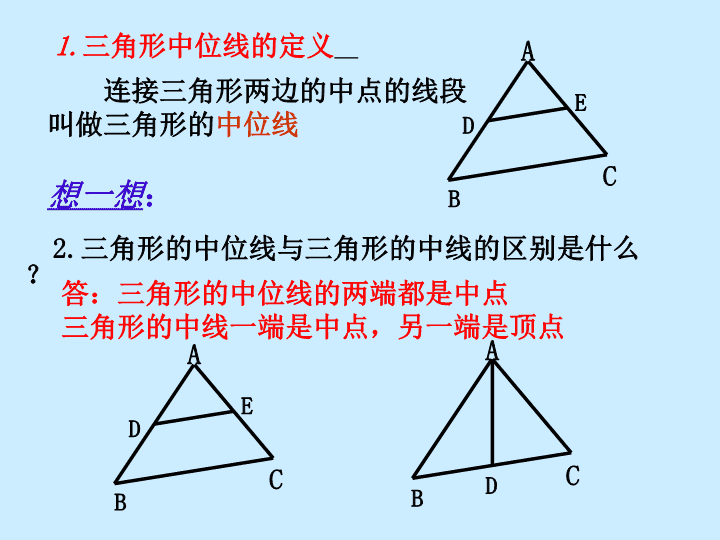
9.5三角形的中位线 温旧呈新1.已知AD是ΔABC的中线，（1）如果BD=3cm,则BC=,如果S△ABC=12cm2,则S△ABD=.（2）如果AB=AC,∠BAC=800,则∠BAD=,∠ADC=.（3）如果∠BAC=900,AD=3,则BC=.2.下面我们一起来探讨“三角形的中位线”CABD 1.三角形中位线的定义连接三角形两边的中点的线段叫做三角形的中位线2.三角形的中位线与三角形的中线的区别是什么？答：三角形的中位线的两端都是中点三角形的中线一端是中点，另一端是顶点想一想：CABDACBDEACBDE 1.剪一个三角形，记为ΔABC2．分别取AB、AC的中点D、E，并连接DE3．沿DE将ΔABC剪成两部分，并将ΔADE绕点E旋转180°得四边形DBCF1.操作：四边形DBCF是什么特殊的四边形？为什么？2.思考：答：四边形DBCF是平行四边形。由操作可知：ΔADE与ΔCFE关于点E成中心对称则CF=AD,∠F=∠ADE由∠F=∠ADE可得：AB∥CF又由CF=AD，AD=DB可得：DB=CF所以四边形BCFD是平行四边形理由：一组对边平行且相等的四边形是平行四边形情景创设 议一议：ΔABC的中位线DE与BC有怎样的位置和数量关系？为什么？答：DE∥BC，DE=½BC通过探索得知：四边形BCFD是平行四边形则DF∥BCDF=BC即DE∥BCDE=½DF=½BC三角形中位线的性质:三角形的中位线平行于第三边，并且等于第三边的一半。说明：此性质的特点：同一条件下有2个结论因为DE为ΔABC的中位线所以①DE∥BC，②DE=½BC↓↓位置关系数量关系 学以致用1.如图（1）ΔABC中，AB=6㎝，AC=8㎝，BC=10㎝，D﹑E﹑F分别是AB、AC、BC的中点，则ΔDEF的周长是＿＿，面积是＿＿.请找出图中的平行四边形。FABcDE(1) 学以致用2.（2016·北京）如图，在四边形ABCD中，∠ABC=900,AC=AD,M、N分别为AC、CD的中点，连接BM、MN、BN.（1）求证：BM=MN;（2）∠BAD=600,AC平分∠BAD,AC=2,求BN的长。ACBNDM 合作探究例1.在四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA的中点.求证：四边形EFGH是菱形延伸：你能用一句话来总结本题的规律吗？规律：依次连接对角线相等的四边形的四边中点形成的四边形是菱形。 合作探究例2.如图，四边形ABCD中，E、F、G、H分别是AB、BC、CD、AD的中点，且对角线AC⊥BD,请探索四边形EFGH的形状并说明理由。ABCDHEFG规律：依次连接对角线互相垂直的四边形的四边中点形成的四边形是矩形。延伸：你能用一句话来总结本题的规律吗？ 活学活用：1.（2015·滨州）顺次连接矩形ABCD各边中点，所得四边行必定是（）A.邻边不等的平行四边形B.矩形C.正方形D.菱形2.（2015·资阳）若顺次连接四边形ABCD各边中点得到一个矩形，则四边行ABCD一定是（）A.矩形B.菱形C.对角线相等的四边形D.对角线互相垂直的四边形 展现自我：3.（2016·德州改编）如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点。（1）请判断四边形EFGH的形状，并说明理由。（2）如果要使四边形EFGH为正方形，那么四边形ABCD的对角线应满足什么条件？不需要说明理由。HGFEDCBA规律：1.依次连接对角线既不相等也不互相垂直的四边形的四边中点形成的四边形是平行四边形。2.依次连接对角线互相垂直且相等的四边形的四边中点形成的四边形是正方形。 规律：1.依次连接对角线相等的四边形的四边中点形成的四边形是菱形。2.依次连接对角线互相垂直的四边形的四边中点形成的四边形是矩形。3.依次连接对角线既不相等也不互相垂直的四边形的四边中点形成的四边形是平行四边形。4.依次连接对角线互相垂直且相等的四边形的四边中点形成的四边形是正方形。（请同学们课后探讨理由）小节：依次连接四边形四边中点形成的四边形与四边形对角线是否相等和垂直有关，与对角线是否平分无关。 本课小结１．理解三角形中位线的概念：连接三角形两边的中点的线段叫做三角形的中位线。２．掌握三角形中位线的性质：三角形的中位线平行与第三边，并且等于第三边的一半。3.能应用三角形中位线的性质解决有关计算或说理等问题。4．能理解依次连接四边形的四边中点形成的四边形的规律。 当堂检测：HEFDGCBA第1题EFDCAB第2题1．（2015·无锡）如图，矩形ABCD的对角线长为8cm，E、F、G、H分别是AB、BC、CD、DA的中点，则四边形EFGH的周长为cm.2．如图，Rt△ABC中，∠C=90°，点D、E、F分别是△ABC三边中点，DE=4cm，则CF=cm。 当堂检测：CBAFEMD第3题3.（2016·陕西）如图，在△ABC中，∠ABC=900，AB=8,BC=6,若DE是△ABC的中位线，延长DE交△ABC的外角∠ACM的平分线于点F，则线段DF的长为（）A.7B.8C.9D.10 当堂检测：BHFGEDC第4题A4.如图，在四边形ABCD中，AB=DC,E、F、G、H分别是AD、BC、BD、AC的中点，四边形EGFH是怎样的四边形？证明你的结论。 课后作业：1.书88页习题9.52.练习册9.5对应部分3.请同学们课后继续探讨本节课遗留下来的疑问。