八年级下数学课件八下第九章9-5三角形的中位线_苏科版

八年级下数学课件八下第九章9-5三角形的中位线_苏科版

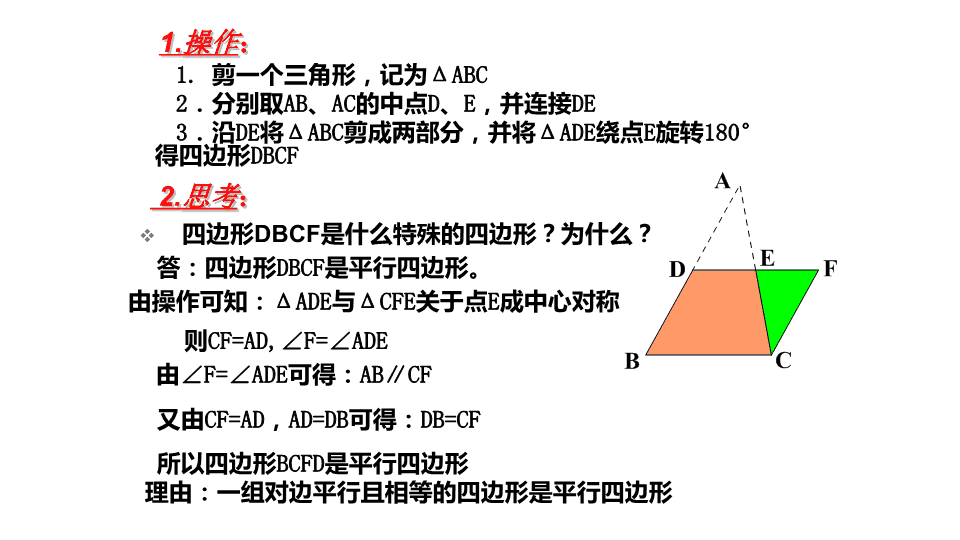
9.5三角形的中位线 情景创设怎样将一张三角形纸片剪成两部分，使分成的两部分能拼成一个平行四边形？ 1.剪一个三角形，记为ΔABC2．分别取AB、AC的中点D、E，并连接DE3．沿DE将ΔABC剪成两部分，并将ΔADE绕点E旋转180°得四边形DBCF1.操作：四边形DBCF是什么特殊的四边形？为什么？2.思考：答：四边形DBCF是平行四边形。由操作可知：ΔADE与ΔCFE关于点E成中心对称则CF=AD,∠F=∠ADE由∠F=∠ADE可得：AB∥CF又由CF=AD，AD=DB可得：DB=CF所以四边形BCFD是平行四边形理由：一组对边平行且相等的四边形是平行四边形 3.三角形中位线的概念连接三角形两边的中点的线段叫做三角形的中位线三角形的中位线与三角形的中线的区别是什么？答：三角形的中位线的两端都是中点三角形的中线一端是中点，另一端是顶点想一想： 议一议：ΔABC的中位线DE与BC有怎样的位置和数量关系？为什么？答：DE∥BC，DE=½BC通过探索得知：四边形BCFD是平行四边形则DF∥BCDF=BC即DE∥BCDE=½DF=½BC三角形中位线的性质:三角形的中位线平行与第三边，并且等于它的一半。说明此性质的特点：同一条件下有2个结论因为DE为ΔABC的中位线所以①DE∥BC，②DE=½BC↓↓位置关系数量关系 例题讲解例1.在四边形ABCD中，AC=BD，E、F、G、H分别是AB、BC、CD、DA的中点.求证：四边形EFGH是菱形∵E、F分别是AB、BC的中点∴EF=1/2AC理由：三角形的中位线平行于第三边,并且等于它的一半同理:FG=BD/2，GH=AC/2，HE=BD/2.∵AC=BD∴四边形EFGH是菱形理由：一四边相等的四边形是菱形.∴EF=FG=GH=HE证明： 例题解析猜一猜：画一个任意四边形，并画出四边的中点，再顺次连接四边形的中点，得到的四边形的形状是什么？如图，四边形ABCD中，EFGH分别是ABCDADBC的中点，四边形EFGH是平行四边形吗？为什么？解：四边形EFGH是平行四边形连接DB因为E、H分别是AB、AD的中点，即EH是ΔABD的中位线所以EH∥BD，EH=½BD，理由是：三角形的中位线平行于第三边，并且等于它的一半。同理可得，FG∥BDFG=½BD所以EH∥FG，EH=FG故四边形EFGH是平行四边形，理由是；一组对边平行且相等的四边形是平行四边形ABCDHEFG ⑴顺次连接任意四边形四边中点所得的四边形是平行四边形议一议：顺次连接矩形的四边中点所得的四边形是什么形状？为什么？如果将“矩形”改成“菱形”呢？⑵顺次连接矩形的四边中点所得的四边形是菱形⑶顺次连接菱形的四边中点所得的四边形是矩形结论：(1)(2)(3) 议一议：1.如果顺次连接四边形四边中点所得的四边形是菱形，那么原四边形的两条对角线存在什么关系？（两条对角线相等）2.上问中的菱形改为矩形呢？（两条对角线互相垂直）3.当四边形满足什么条件时，顺次连接它的四边中点所得的四边形是正方形？（两条对角线互相垂直且相等） 课堂训练1.如图（1）ΔABC中，AB=6㎝，AC=8㎝，BC=10㎝，D﹑E﹑F分别是AB、AC、BC的中点，则ΔDEF的周长是＿＿，面积是＿＿.2.如图（2）ΔABC中，DE是中位线，AF是中线，则DE与AF的关系是＿＿＿＿3.若顺次连接四边形四边中点所得的四边形是菱形，则原四边形（　）（A）一定是矩形（B）一定是菱形（C）对角线一定互相垂直　（D）对角线一定相等FABcDE(1)ACBDEF(2)互相平分6cm212cmD ４．如图,梯形ABCD中，AD∥BC，E﹑F分别是AC﹑BD的中点（１）EF与AD﹑BC的关系如何？为什么？（２）若AD=a，BC=b，求EF的长。ABCDEFG解：（１）AD∥EF∥BC因为AD∥BC，则∠DAF＝∠GCF，∠ADF＝∠CGF连接DF并延长DF交BC于G又AF＝FC所以△ADF≌△CFG(AAS)所以DF=FG而DE=EB所以EF∥BC理由是：三角形的中位线平行于第三边又AD∥BC所以AD∥EF∥BC 5．如图,梯形ABCD中，AD∥BC，E﹑F分别是AC﹑BD的中点（１）EF与AD﹑BC的关系如何？为什么？（２）若AD=a，BC=b，求EF的长。AEGDFCB解：（2）所以EF=BG=½(BC-GC)理由是：三角形的中位线等于第三边的一半。而GC=AD所以EF=½(BC-AD)=½(b-a)由（１）可知：EF是△DBG的中位线 探索研究：已知：△ABC的周长为a，面积为s，连接各边中点得△A1B1C1，再连接△A1B1C1各边中点得△A2B2C2……，则（１）第３次连接所得△A3B3C3的周长＝＿＿＿＿,面积＝＿＿＿＿（２）第n次连接所得△AnBnCn的周长＝＿＿＿＿，面积＝＿＿＿＿ABC次序123……n所得三角形周长……得三角形面积所……A１B１C１A２B２C２分析：填表 本课小结１．理解三角形中位线的概念：连接三角形两边的中点的线段叫做三角形的中位线。２．掌握三角形中位线的性质：三角形的中位线平行与第三边，并且等于它的一半。3．能应用三角形中位线的性质解决有关计算或说理等问题。