八年级下数学课件：19-1-2 函数的图象 （共16张PPT）_人教新课标

八年级下数学课件：19-1-2 函数的图象 （共16张PPT）_人教新课标

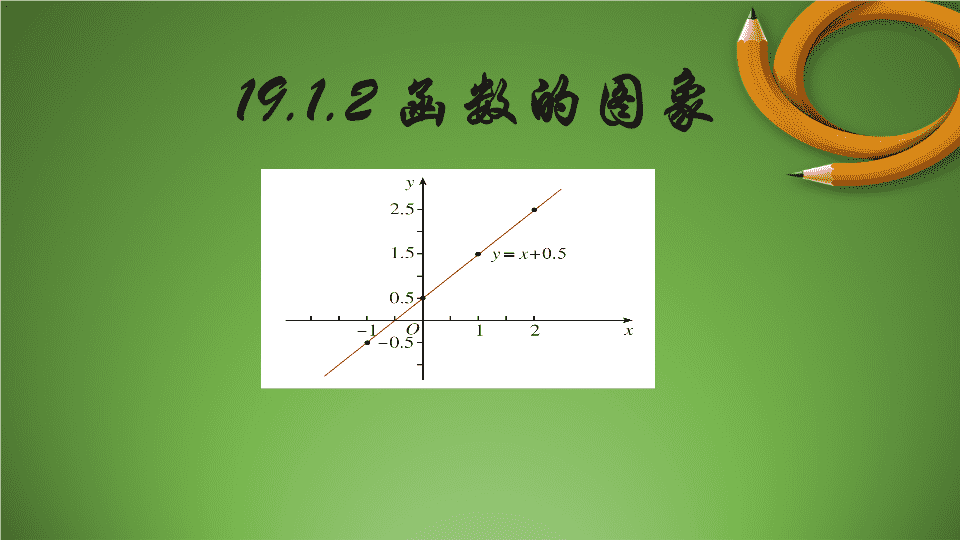
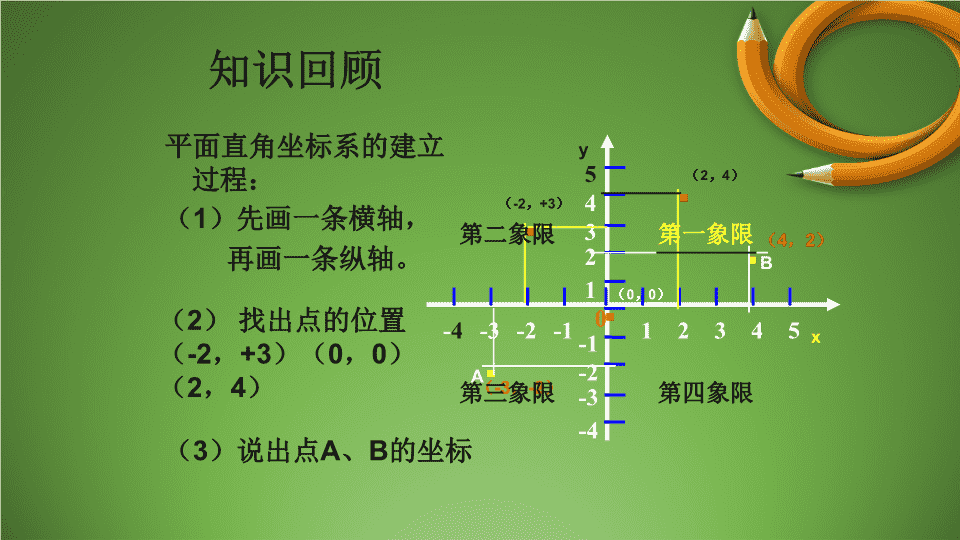
19.1.2函数的图象 2.什么是函数、函数值？1.什么叫常量、变量？试举例说明。在一个变化过程中，数值发生变化的量为变量。在一个变化过程中，数值始终不变的量为常量。在一个变化过程中，如果有两个变量x与y,并且对于x的每一个确定的值，y都有唯一确定的值与其对应，那么我们就说x是自变量，y是x的函数。如果当x=a时y=b，那么b叫做当自变量x的值为a时的函数值。温故知新 知识回顾平面直角坐标系的建立过程：（1）先画一条横轴，再画一条纵轴。31425-2-4-1-3012345-4-3-2-1xy（2）找出点的位置（-2，+3）（0，0）（2，4）————————·（-2，+3）·（0，0）——————————·（2，4）··AB（3）说出点A、B的坐标（-3，-2）（4，2）第一象限第二象限第三象限第四象限________________________________________ 下图是某日的气温变化图．气温曲线上每一点（t，T）表示时间为t时的气温是T_________________(10,2)___________________(14,5)________ 探究新知问题：气温曲线是图象表示函数的一个实际例子。那么什么是函数图象呢？一般地，对于一个函数，如果把自变量x与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点组成的图形，就是这个函数的图像 例1．在下列式子中，对于x的每一确定的值，y有唯一的对应值，即y是x的函数，画出这些函数的图象： 解：x…-3-2-10123…y……-2-101234根据表中数值描点（x，y），并用平滑曲线连接这些点（如上图）．从函数图象可以看出，直线从左到右上升，即当x由小到大时，y=x+1随之增大．-6o-446246-2-2-4xy2······· 列表：x…0.511.522.533.5456…y…1…6321.5根据表中数值描点（x，y），并用平滑曲线连接这些点（如图）．从函数图象可以看出，直线从左到右下降，即当x由小到大时，y=6/x随之减小． 描点法画函数图象的一般步骤：第一步：列表．在自变量取值范围内选定一些值．通过函数关系式求出对应函数值列成表格．第二步：描点．在直角坐标系中，以自变量的值为横坐标，相应函数值为纵坐标，描出表中对应各点．第三步：连线．按照坐标由小到大的顺序把所有点用平滑曲线连结起来． 解：取自变量x的一些值，例如x＝－3，－2,－1，0，1，2，3…，计算出对应的函数值．为表达方便，可列表如下：由这一系列的对应值，可以得到一系列的有序实数对：…，（－3，4.5），（－2，2），（－1，0.5），（0，0），（1，0.5），（2，2），（3，4.5），…x…………y-34.5-22-10.50.50012234.5例1：画出函数y=x的图象1—22 ●●●●●●●x…-3-2-10123…y…4.520.500.524.5…画函数图象的步骤：一、列表二、描点三、连线强调：1、描点画出的函数图象是局部的近似的，要注意在所画出的曲线两端稍作延伸。y=x1_222、选点的个数及描点的准确、连线的光滑都影响图象的准确度，画图时应用铅笔画图。_________________________________________________3、画图时要从左往右画 不同的函数具有不同的图象y=x1_22y=x1_2y=-6_x 2、画出函数y=-的图象解：列表如下：￣6xx…-4-3-2-1…1234…y…1.5236…-6-3-2-1.5…y-14321Ox-2-3-4-1-21234.5......连线:用光滑的曲线连线，就可得函数的图象了。6-3-4-5-6.描点:y=-6_x为什么没有“0”？ 回顾与小结这节课你学到了什么？ 1．画实际问题的图象时，必须先考虑函数自变量的取值范围．有时为了表达的方便，建立直角坐标系时，横轴和纵轴上的单位长度可以取得不一致．2．在观察实际问题的图象时，先从两坐标轴表示的实际意义得到点的坐标的实际意义．然后观察图形，分析两变量的相互关系，给合题意寻找对应的现实情境．课堂小结 再见谢谢！