三角形的外角和教案2

三角形的外角和教案2

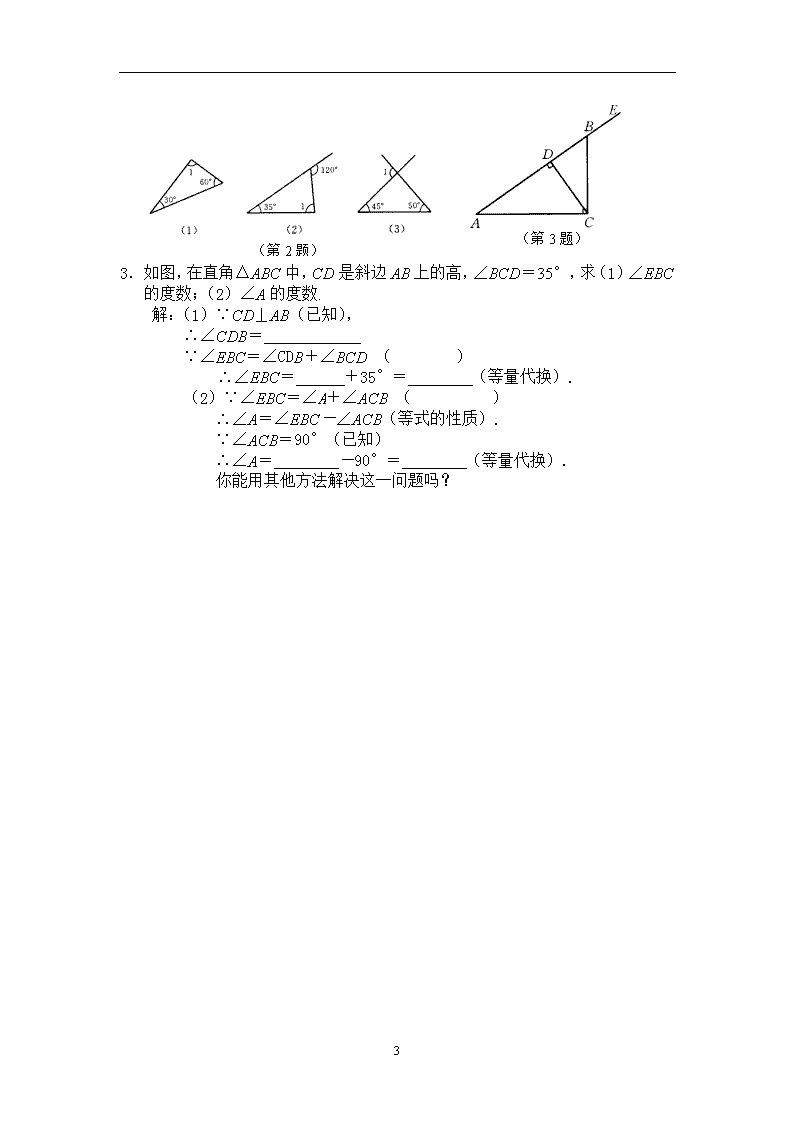
‎ ‎ ‎9.1.2三角形的外角和 我们已经知道三角形的内角和等于180°． 现在我们讨论三角形的外角及外角和． 如图9.1.8所示，一个三角形的每一个外角对应一个相邻的内角和两个不相 邻的内角．‎ 三角形的外角与内角有什么关系呢？‎ 在图9.1.9中，显然有 ∠CBD（外角）＋∠ABC（相邻内角）＝180°．‎ 那么外角∠CBD与其他两个不相邻的内角又有什么关系呢？‎ 做一做 在一张白纸上画出如图9.2.7所示的图形，然后把∠ACB、∠BAC剪下拼在一起，放到∠CBD上，看看会出现什么结果，与你的同伴交流一下，结果是否一样.‎ 可以发现∠CBD＝∠ACB＋∠BAC，‎ 实际上，因为 ‎∠CBD＋∠ABC＝180°‎ ‎∠ACB＋∠BAC＋∠ABC＝180°‎ 比较这两个式子，就可以得到你与你的同伴所发现的结论.‎ 由此可知，三角形的外角有两条性质：‎ 1. 三角形的一个外角等于与它不相邻的两个内角的和；‎ 2. 三角形的一个外角大于任何一个与它不相邻的内角.‎ 与三角形的每个内角相邻的外角分别有两个，这两个外角是对顶角.从与每 个内角相邻的两个外角中分别取一个相加，得到的和称为三角形的外角和.如图9.1.10所示，∠1＋∠2＋∠3就是△ABC的外角和.‎ 做一做 在图9.1.10中 ‎∠1＋______________=180°,‎ ‎∠2+_______________=180°,‎ ‎∠3+_______________=180°.‎ 3‎ ‎ ‎ 三式相加可以得到 ‎∠1＋∠2＋∠3＋______+______+______=_______,（1）‎ 而　　　　　∠ACB＋∠BAC＋∠ABC＝180°，　　　 （2）‎ 将（1）与（2）相比较，你能得出什么结论？‎ 概括 可以得到 ‎∠1＋∠2＋∠3＝360°‎ 由此可知：三角形的外角和等于360°.‎ 例1 如图9.1.11，D是△ABC的BC边上一点，∠B＝∠BAD，∠ADC＝80°，∠BAC=70°.求：‎ ‎（1）∠B的度数；‎ ‎（2）∠C的度数.‎ 解　（1）∵∠ADC是△ABD的外角（已知），∴‎ ‎∠ADC＝∠B＋∠BAD＝80°（三角形的一个外角等于与它不相邻的两个内角的和）.‎ 又　　　∠B＝∠BAD（已知），‎ ‎∴　　∠B＝80°×＝40°（等量代换）.‎ ‎（2）在△ABC中，∵∠B＋∠BAC＋∠C＝180°（三角形的内角和等于180°），‎ ‎∴　　∠C＝180°－∠B－∠BAC（等式的性质）‎ ‎＝180°－40°－70°‎ ‎＝70°‎ 练 习 ‎1.（口答）一个三角形可以有两个内角都是直角吗？可以有两个内角都是钝角或都是锐角吗？为什么？‎ ‎2.求下列各图中∠1的度数.‎ 3‎ ‎ ‎ 3． 如图，在直角△ABC中，CD是斜边AB上的高，∠BCD＝35°，求（1）∠EBC的度数；（2）∠A的度数.‎ 解：（1）∵CD⊥AB（已知），‎ ‎∴∠CDB＝ ‎ ‎∵∠EBC＝∠CDB＋∠BCD （ ）‎ ‎∴∠EBC＝ ＋35°＝ （等量代换）.‎ ‎（2）∵∠EBC＝∠A＋∠ACB （ ）‎ ‎∴∠A＝∠EBC－∠ACB（等式的性质）.‎ ‎∵∠ACB＝90°（已知）‎ ‎∴∠A＝ －90°＝ （等量代换）.‎ 你能用其他方法解决这一问题吗？‎ 3‎