两条直线的位置关系教案(第课时)_　　

两条直线的位置关系教案(第课时)_　　

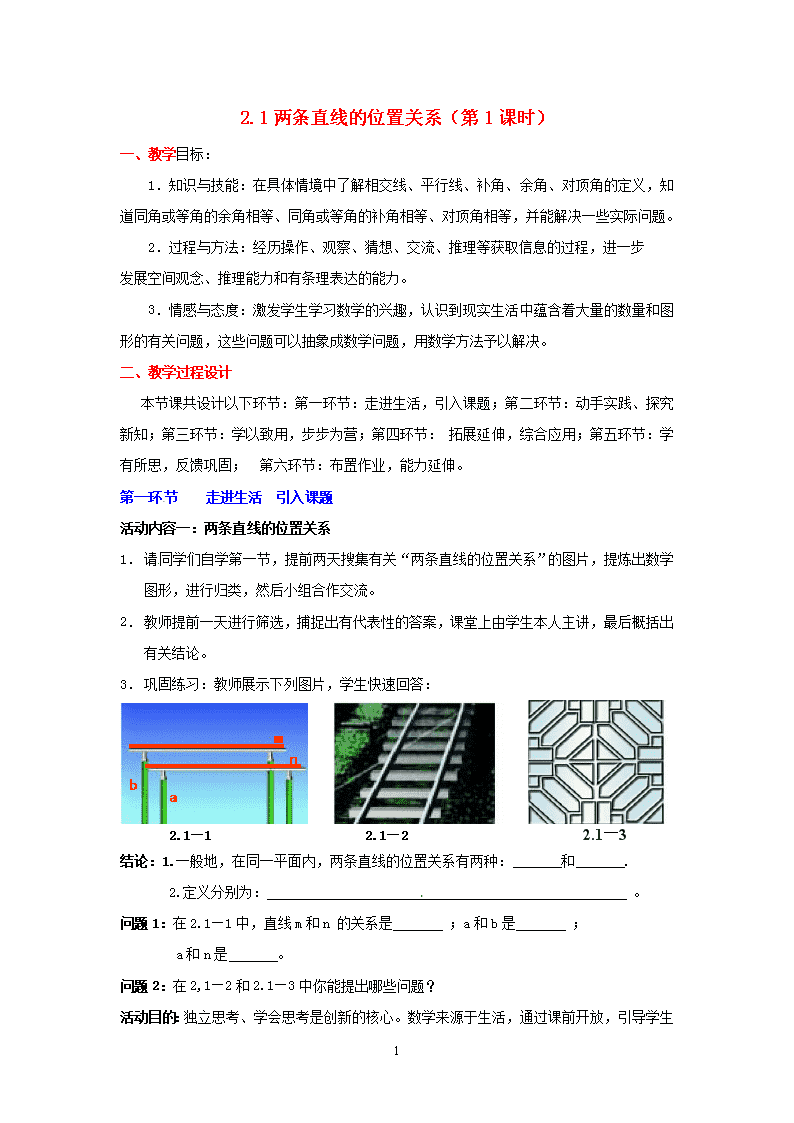
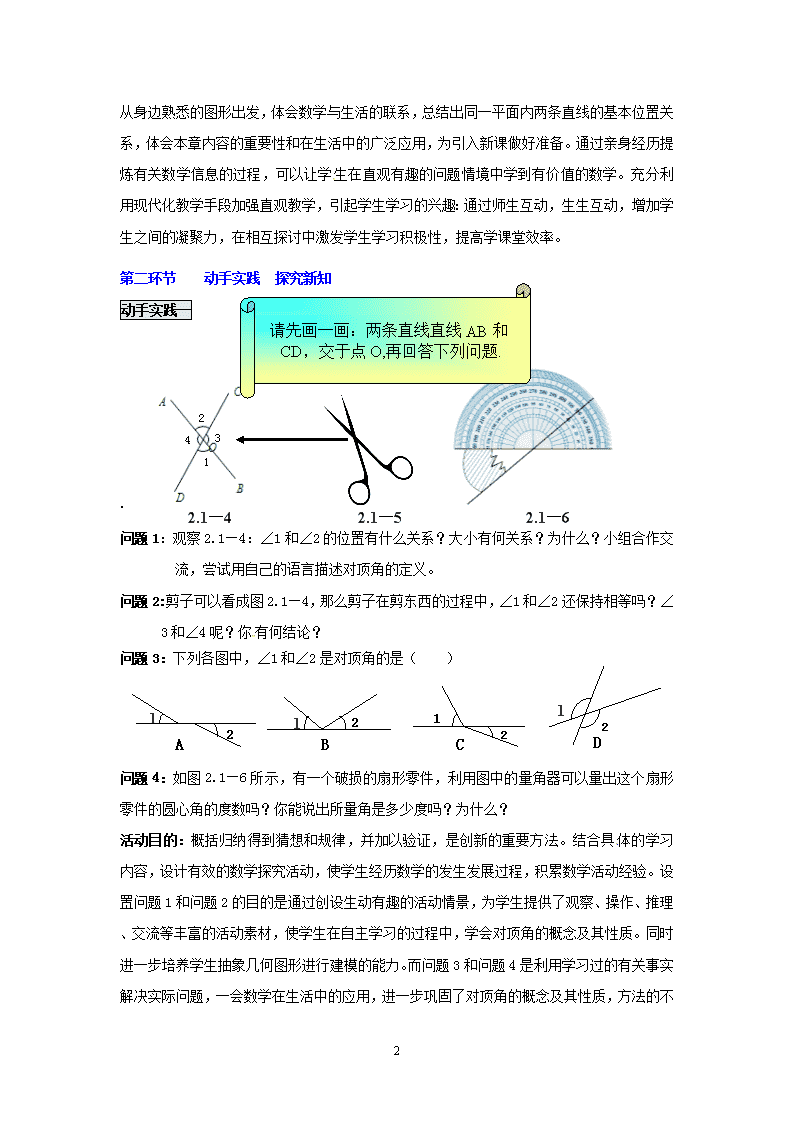
‎ ‎ ‎2.1两条直线的位置关系（第1课时） ‎ 一、教学目标：‎ ‎1．知识与技能：在具体情境中了解相交线、平行线、补角、余角、对顶角的定义，知道同角或等角的余角相等、同角或等角的补角相等、对顶角相等，并能解决一些实际问题。‎ ‎2．过程与方法：经历操作、观察、猜想、交流、推理等获取信息的过程，进一步发展空间观念、推理能力和有条理表达的能力。‎ ‎3．情感与态度：激发学生学习数学的兴趣，认识到现实生活中蕴含着大量的数量和图形的有关问题，这些问题可以抽象成数学问题，用数学方法予以解决。‎ 二、教学过程设计 本节课共设计以下环节：第一环节：走进生活，引入课题；第二环节：动手实践、探究新知；第三环节：学以致用，步步为营；第四环节： 拓展延伸，综合应用；第五环节：学有所思，反馈巩固； 第六环节：布置作业，能力延伸。‎ 第一环节　 走进生活 引入课题 活动内容一：两条直线的位置关系 1． 请同学们自学第一节，提前两天搜集有关“两条直线的位置关系”的图片，提炼出数学图形，进行归类，然后小组合作交流。‎ 2． 教师提前一天进行筛选，捕捉出有代表性的答案，课堂上由学生本人主讲，最后概括出有关结论。‎ 3． 巩固练习：教师展示下列图片，学生快速回答：‎ ‎2.1—3‎ m n a b ‎ ‎ ‎ 2.1—1 2.1—2 ‎ 结论：1.一般地，在同一平面内，两条直线的位置关系有两种： 和 .‎ ‎ 2.定义分别为： 。‎ 问题1：在2.1—1中，直线m和n 的关系是 ；a和b是 ；‎ a和n是 。‎ 问题2：在2,1—2和2.1—3中你能提出哪些问题？‎ 活动目的：独立思考、学会思考是创新的核心。‎ 6‎ ‎ ‎ 数学来源于生活，通过课前开放，引导学生从身边熟悉的图形出发，体会数学与生活的联系，总结出同一平面内两条直线的基本位置关系，体会本章内容的重要性和在生活中的广泛应用，为引入新课做好准备。通过亲身经历提炼有关数学信息的过程，可以让学生在直观有趣的问题情境中学到有价值的数学。充分利用现代化教学手段加强直观教学，引起学生学习的兴趣：通过师生互动，生生互动，增加学生之间的凝聚力，在相互探讨中激发学生学习积极性，提高学课堂效率。‎ 请先画一画：两条直线直线AB和CD，交于点O,再回答下列问题.‎ 第二环节　 动手实践 探究新知 动手实践一 ‎.‎2.1—5‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎2.1—4‎ ‎2.1—6‎ ‎ 问题1：观察2.1—4：∠1和∠2的位置有什么关系？大小有何关系？为什么？小组合作交流，尝试用自己的语言描述对顶角的定义。‎ 问题2:剪子可以看成图2.1—4，那么剪子在剪东西的过程中，∠1和∠2还保持相等吗？∠3和∠4呢？你有何结论？‎ 问题3：下列各图中，∠1和∠2是对顶角的是（ ）‎ ‎1‎ ‎2‎ ‎1‎ ‎2‎ ‎1‎ ‎2‎ ‎1‎ ‎2‎ A B C D 问题4：如图2.1—6所示，有一个破损的扇形零件，利用图中的量角器可以量出这个扇形零件的圆心角的度数吗？你能说出所量角是多少度吗？为什么？‎ 活动目的：概括归纳得到猜想和规律，并加以验证，是创新的重要方法。结合具体的学习内容，设计有效的数学探究活动，使学生经历数学的发生发展过程，积累数学活动经验。‎ 6‎ ‎ ‎ 设置问题1和问题2的目的是通过创设生动有趣的活动情景，为学生提供了观察、操作、推理、交流等丰富的活动素材，使学生在自主学习的过程中，学会对顶角的概念及其性质。同时进一步培养学生抽象几何图形进行建模的能力。而问题3和问题4是利用学习过的有关事实解决实际问题，一会数学在生活中的应用，进一步巩固了对顶角的概念及其性质，方法的不唯一激发了学生的兴趣。‎ 动手实践二 注意：互余与互补是指两个角之间的数量关系，与它们的位置无关。‎ 补角定义：一般地，如果两个角的和是1800，那么称这两个角互为补角（supplementary angle）‎ 余角定义：‎ 如果两个角的和是900，那么称这两个角互为余角（complementary angle）‎ 活动目的：通过动手画图，可以加深学生对概念的理解，在相互交流中，初步形成评价与反思的意识，在相互补充、相互学习中，体验“互补互余”仅仅表明了两个角的度量关系，并没有限制角的位置关系；在合作共赢中，获得成功的乐趣，锻炼克服困难的意志，建立自信心，可以更好地掌握新知识。‎ 巩固反馈：‎ 问题1：小组合作，每人编一道有关余角或者补角的题目，其余同学抢答，组长记录、整理各种题型，练习2分钟。教师巡视，给予评价，捕捉好资源。‎ 问题2：教师将捕捉到的好资源用投影仪集体展示，全班抢答，及时给予评价。‎ 问题3：下列说法中，正确的有 。（填序号）‎ ① 已知∠A=40º，则∠A的余角=500②若∠1+∠2=90º，则∠1和∠2互为余角。‎ ‎③若∠1+∠2+∠3=180º，则∠1、∠2和∠3互为补角。④若∠A=40º26′，则∠A的补角=139º34′⑤一个角的补角必为钝角。⑥一个锐角的补角比这个角的余角大900‎ 活动目的：据学生活泼好动、争强好胜的心理，设置问题1和问题2可以更好地激发学生的参与意识，在竞争中加深对概念的理解，提升所编题的质量，促进合作交流的意识。问题3是针对学生易错题而改编的一组判断题，这种形式能引导学生逐步加深对余角、补角的概念及其性质的理解和掌握。‎ 动手实践三 ‎ 打台球时，选择适当的方向，用白球击打红球，反弹后的红球会直接入袋，此时∠1=∠2，将图2.1—7抽象成图2.1—8，ON与DC交于点O，∠DON=∠CON=900，∠1=∠2‎ 6‎ ‎ ‎ ‎2.1—7‎ ‎2‎ D C O ‎1‎ ‎3‎ ‎4‎ A N B ‎2.1—8‎ 同角或者等角的余角相等。‎ 同角或者等角的补角相等。‎ 小组合作交流，解决下列问题：在图2.1—8中 问题1：哪些角互为补角？哪些角互为余角？‎ 问题2：∠3与∠4有什么关系？为什么？‎ 问题3：∠AOC与∠BOD有什么关系？为什么？‎ 你还能得到哪些结论？‎ 活动目的：概括归纳得到猜想和规律，并加以验证，是创新的重要方法。通过生动有趣的活动情景，为学生提供了观察、操作、推理、交流等丰富的数学活动，使学生在自主学习的过程中，掌握“同角或者等角的补角相等。”“同角或者等角的余角相等。”并能够用自己的语言说出简单推理。同时发散学生思维，让学生尽可能用多种方法来说明自己猜测的正确性，培养学生合情说理的能力。并在这个过程中，培养学生抽象几何图形进行建模的能力。本着面向全体的原则，从学生生活经验和熟悉的背景知识出发，通过创设情境串---问题串，极大的调动全体学生的参与意识，充分挖掘他们的潜能，给学生一个充分展示的舞台，以达到人人都能学好数学的目标！‎ 第三环节 学以致用，步步为营 A B C ‎2.1—9‎ A B C ‎2.1—10‎ D 问题1：①.因为∠1+∠2=90º，∠2+∠3=90º，所以∠1= ，理由是 .‎ ‎② 因为∠1+∠2=180º，∠2+∠3=180º，所以∠1= ，理由是 .‎ 问题2：‎ ‎①用你手中的三角板，画一个直角三角形，如图2.1—9.则∠A是∠B的 。‎ 变式训练：‎ ① 在①的基础上，做∠CDA=900。如图2.1—10.‎ 1. 则∠A的余角有哪几个？为什么？‎ 2. 请找出互补的角，并说明理由。‎ 6‎ ‎ ‎ 1. 你还能提出哪些问题？试试看吧！‎ 活动目的：通过一题多变，可以引导学生透过现象看本质、通过本质找规律、通过规律找方法。重视动手操作，是发展学生思维，培养学生数学能力最有效途径之一。通过亲自画图，可以直观的发现有关结论，它有利于让学生参与知识的形成过程，促进对抽象数学的理解，为问题的顺利解决而奠定基础。变式训练题的设置更能激发学生的兴趣，在超级变变变中体验数学的美，学会从不同的角度看待问题。‎ ‎2.1—12‎ O D E C B A O B A C D E ‎2.1—11‎ 第四环节 拓展延伸，综合应用 ‎ 问题1：如图2.1—11已知：直线AB与CD交于点O, ∠EOD=900,回答下列问题：‎ ‎1. ∠AOE的余角是 ；补角是 。‎ ‎2. ∠AOC的余角是 ；补角是 ；对顶角是 。‎ 问题2：如图2.1—12，点O在直线AB上，∠DOC和∠BOE都等于900.‎ 请找出图中互余的角、互补的角、相等的角，并说明理由。先独立探究，再小组交流。‎ 活动目的：通过问题串的巧妙设置，不仅高效率的复习了本节的知识点，而且让学生在开放的环境中畅所欲言，收获了一份自信！问题串的设置提高了学生的探索意识和创新意识的形成，激发了学生的学习兴趣和探究欲。‎ 第五环节 学有所思 反馈巩固 归纳总结：‎ 1. 你学到了哪些知识点？‎ 2. 你学到了哪些方法？‎ 3. 你还有哪些困惑？‎ 活动目的：本环节的设置使学生学会从系统的角度把握知识方法，努力使知识结构化、网络化，引导学生时刻注意新旧知识之间的联系；鼓励学生畅谈自己学习的知识和体会，激发学生对数学的学习兴趣与信心，培养学生独自梳理知识，归纳学习方法及解题方法的能力。锻炼学生组织语言及表达能力，经历与同伴分享成果的快乐过程。‎ 巩固反馈 ‎1. 如图2.1-13，直线AB与CD交于点O，∠BOC=900，EF经过点O.‎ ‎（1）指出图中所有的对顶角；‎ O A B ‎2.1—15‎ ‎（2）图中那些角与∠AOE互余？互补？‎ ‎（3）若∠BOF=34°，试求出∠AOF，∠BOE，∠DOE的度数.‎ 6‎ ‎ ‎ ‎2.1—13‎ O A B C D E ‎2.1—14‎ ‎2.如图2.1—14，点O在直线AB上，OC平分∠BOD，OE平分∠AOD，请找出∠COD的余角和补角，并说明理由。‎ ‎3.学以致用： 如图2.1—15：小颖想测量一堵拐角高墙在底面上所成的角∠AOB度数，人不能进入围墙内，你能帮小颖想出简单的测量方法吗？请简述你的方法。‎ 活动目的：巩固本节课的知识点，检验学生的掌握程度。‎ 第六环节 布置作业 能力延伸 基础题：1．书P42页习题2.1 第 1,2,3,4,5题 C A B D E F 提高题：2.下图由两块相同的直角三角板拼成，其中∠FDE=∠AOB=900，点O在FD上，DE在直线AB上， 请找出相等的角、互余的角、互补的角。‎ 活动目的：作业应该体现出课堂学习的延续性，因此本节课我也精心设计了一道探究性的题目，实现了同一图形经过不同变化可以产生不同问题，与课堂的问题相呼应；作业分层，可以让不同程度的学生都能有不同的收获。‎ 三、教学反思：‎ 6‎