七年级上册数学课件《求解一元一次方程》 (2)_北师大版 (1)

七年级上册数学课件《求解一元一次方程》 (2)_北师大版 (1)

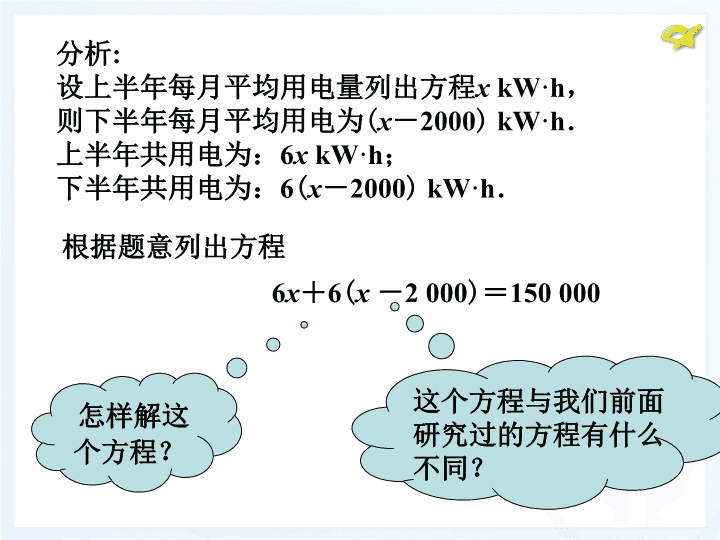
问题1：某工厂加强节能措施，去年下半年与上半年 相比，月平均用电量减少2 000 kW·h(千瓦·时）， 全年用电15 万 kW·h.这个工厂去年上半年每月平均 用电是多少？ 温馨提示：1 kW·h的电量是指1 kW的电器1 h的用电量. 思考： 1.题目中涉及了哪些量？ 2.题目中的相等关系是什么？ 月平均用电量×n(月数)＝n个月用电量 上半年的用电量＋下半年的用电量＝全年的用电量 （一）提出问题，建立模型 6x＋6(x －2 000)＝150 000 分析: 设上半年每月平均用电量列出方程x kW·h， 则下半年每月平均用电为(x－2000) kW·h． 上半年共用电为：6x kW·h； 下半年共用电为：6(x－2000) kW·h． 根据题意列出方程 怎样解这 个方程？ 这个方程与我们前面 研究过的方程有什么 不同？ （二）探究解法，归纳总结 6x＋6(x－2 000)＝150 000 6x＋6x－12 000＝150 000 x＝13 500 去括号 合并同类项 移项 6x＋6x＝150 000＋12 000 系数化为1 12x＝162 000 怎样使方程向x=a 的形式转化？ 怎样解这 个方程？ 注：方程中有带 带括号的式子 时，去括号是 常用的化简步 骤. 问题1：某工厂加强节能措施，去年下半年与上半年 相比，月平均用电量减少2 000 kW·h(千瓦·时）， 全年用电15 万kW·h.这个工厂去年上半年每月平均 用电是多少？ 思考： 本题还有其他列方程的方法吗？ 用其他方法列出的方程应怎样解？ 设上半年平均每月用电x度 列方程 1500002000 6 x x＋ － ＝ 2 2000 25000x－ ＝ 2 27000x＝ 13500x＝ （二）探究解法，归纳总结 问题2：通过以上解方程的过程，你能总结出 含有括号的一元一次方程解法的一般步骤吗？ 去括号 移项 合并同类项 系数化为1 （二）探究解法，归纳总结 思考： 1．行程问题涉及哪些量？它们之间的关系是什么？ 路程、速度、时间． 路程＝速度×时间． 活动2：巩固方法，解决问题 例　一艘船从甲码头到乙码头顺流行驶，用了2 h；从 乙码头返回甲码头逆流行驶，用了2.5 h．已知水流的 速度是3 km/h，求船在静水中的速度. 思考： 2.问题中涉及到顺、逆流因素，这类问题中有哪 些基本相等关系？ 活动2：巩固方法，解决问题 例　一艘船从甲码头到乙码头顺流行驶，用了2 h；从 乙码头返回甲码头逆流行驶，用了2.5 h．已知水流的 速度是3 km/h，求船在静水中的速度. 顺流速度＝静水速度＋水流速度 逆流速度＝静水速度－水流速度 思考： 3．一般情况下可以认为这艘船往返的路程相等， 则顺流速度___顺流时间___逆流速度 ___逆流时间 × ＝ × 活动2：巩固方法，解决问题 例2　一艘船从甲码头到乙码头顺流行驶，用了2 h； 从乙码头返回甲码头逆流行驶，用了2.5 h．已知水流 的速度是3 km/h，求船在静水中的速度. 解：设船在静水中的平均速度为x km/h，则顺流 的速度为(x＋3) km/h，逆流速度为(x－3) km/h. 根据往返路程相等，列出方程，得 2 3 2.5 3x x（ ＋）＝ （ －） 去括号，得 2 6 2.5 7.5x x＋ ＝ － 移项及合并同类项，得 0.5 13.5x＝ 系数化为1，得 27.x  答：船在静水中的平均速度为 27 km/h. 例题 解下列方程： （1）2 ( 10) 5 2( 1)x x x x－ ＋ ＝ ＋ － 解：去括号，得 2 10 5 2 2.x x x x－ － ＝ ＋ － 移项，得 2 5 2 2 10.x x x x－ － － ＝－ ＋ 合并同类项，得 6 8.x ＝ 系数化为1，得 4 . 3 x＝－ （三）熟悉解法，思考辨析 解下列方程： (2) 3 7( 1) 3 2( 3)x x x－ － ＝ － ＋ 解：去括号，得 3 7 7 3 2 6x x x－ ＋ ＝ － － 移项，得 3 7 2 3 6 7x x x＝ ＋ ＝ － － 合并同类项，得 2 10x－ ＝－ 系数化为1，得 5x＝ 例题 （三）熟悉解法，思考辨析 期中数学考试后，小明、小方和小华三名同学对 答案，其中有一道题三人答案各不相同，每个人都认 为自己做得对，你能帮他们看看到底谁做得对吗？做 错的同学又是错在哪儿呢？ 题目：一个两位数，个位上的数是2，十位 上的数是x，把2和x对调，新两位数的2倍 还比原两位数小18，你能想出x是几吗？ 去括号错 移项错 20 2 (10 2) 2( 20) 18 10 2 2 18 10 2 18 20 8 40 5 x x x x x x x x ＋ － ＋ ＝ ＋ － － ＝ － ＝ ＋ ＋ ＝ ＝ 小方： 解： 去括号，得 合并同类项，得 移项，得 系数化为1，得 题目：一个两位数个位上的数是2，十 位上的数是x，把2和x对调，新两位数的2 倍还比原两位数小18，你能想出x是几 吗？ 移项错 2 (10 2) 2( 20) 18 10 2 2 40 18 10 2 18 40 8 60 7.5 x x x x x x x x ＋ － ＋ ＝ ＋ － － ＝ － ＝ ＋ ＋ ＝ ＝ 小华： 解： 去括号，得 合并同类项，得 移项，得 系数化为1，得 题目：一个两位数个位上的数是2，十位上的数是 x，把2和x对调，新两位数的2倍还比原两位数小 18，你能想出x是几吗？ 列方程错 2(20 ) (10 2) 18x x   小明： 40 2 10 2 18 2 10 18 40 2 2 2.5 x x x x x x ＋ － ＋ ＝ ＋ － － ＝ － ＝ － ＋ －8 ＝－ 0 ＝ 解： 去括号，得 合并同类项，得 移项，得 系数化为1，得 一架飞机在两城之间航行，风速为24 km/h，顺风 飞行要2小时50分，逆风飞行要3小时，求两城距离． 解：设飞机在无风时的速度为x km/h， 则在顺风中的速度为(x＋24) km/h ， 在逆风中的速度为（x－24) km/h. 根据题意，得 17 ( 24) 3( 24) 6 x x＋ ＝ － 解得 840.x＝ 3 (840 24) 2 448. － ＝两城市的距离： 答：两城市之间的距离为2 448 km. （四）基础训练，巩固提高 （四）基础训练，巩固提高 2( 3) 5x x＋ ＝ ； 4 3(2 3) 12 ( 4);x x x＋ － ＝ － ＋ 1 16( 4) 2 7 ( 1); 2 3 x x x－ ＋ ＝ － － 2 3( 1) 1 2(1 0.5 ).x x－ ＋ ＝－ ＋ （1） （2） （3） （4） 解下列方程 解：去括号，得 移项，得 合并同类项，得 系数化为1，得 2 6 5 .x x  2 5 6.x x   3 6.x   2.x  2( 3) 5x x （1） 解：去括号，得 移项，得 合并同类项，得 系数化为1，得 4 6 9 12 4.x x x     4 6 9 12 4.x x x     11 17.x  17 . 11 x  4 3(2 3) 12 ( 4)x x x    （2） 解：去括号，得 移项，得 合并同类项，得 系数化为1，得 13 24 2 7 1. 3 x x x     13 2 24 7 1. 3 x x x     16 32. 3 x  6.x  1 16( 4) 2 7 ( 1) 2 3 x x x    （3） 解：去括号，得 移项，得 合并同类项，得 系数化为1，得 2 3 3 1 2 .x x     3 1 2 2 3.x x      2 0.x  0.x  2 3( 1) 1 2(1 0.5 )x x    （4） （五）归纳小结，布置作业 1.本节课你有哪些收获？ 2.你觉得自己掌握这些知识困难吗？ 3.在解决问题时应该注意些什么呢？ 作业： 教科书第98页习题3.3第1，2题.