七年级下册数学课件《平行线的特征综合运用》 (1)_北师大版

七年级下册数学课件《平行线的特征综合运用》 (1)_北师大版

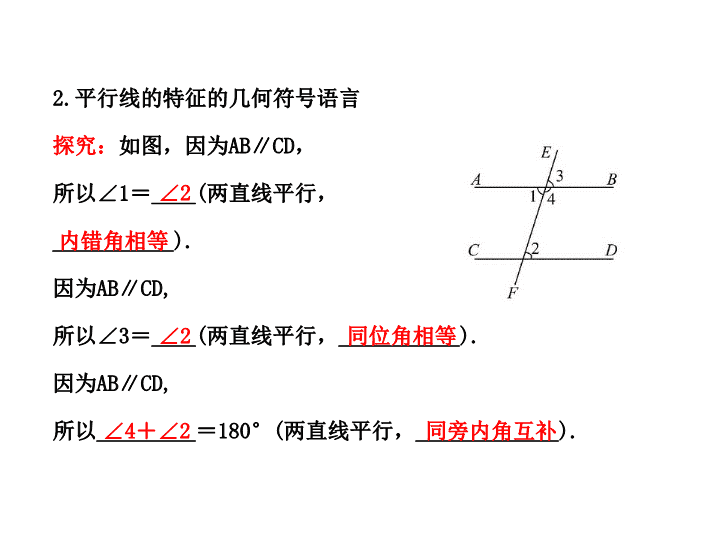
第2课时平行线的性质与判定的综合 1.平行线的特征的文字叙述特征1：两直线平行，同位角_____.特征2：两直线平行，内错角_____.特征3：两直线平行，同旁内角_____.相等相等互补 2.平行线的特征的几何符号语言探究：如图，因为AB∥CD，所以∠1＝____(两直线平行，___________).因为AB∥CD,所以∠3＝____(两直线平行，___________).因为AB∥CD,所以_________＝180°(两直线平行，_____________).∠2内错角相等∠2同位角相等∠4＋∠2同旁内角互补 【预习思考】已经学过的能说明两个角相等的方法有哪些？提示：(1)角平分线.(2)对顶角.(3)余角、补角的性质. 问题1：如图，直线a，b被直线c所截，（1）当∠1=∠2时,你能结合图形用推理的方式来说明a∥b吗？（2）若∠2+∠3=180°呢？ 问题2如图：（1）若∠1=∠2，可以判定哪两条直线平行？根据是什么？（2）若∠2=∠M，可以判定哪两条直线平行？根据是什么？（3）若∠2+∠3=180°，可以判定哪两条直线平行？根据是什么？ 问题3如图，AB∥CD，如果∠1=∠2，那么EF与AB平行吗？说说你的理由． 解：因为∠1=∠2，根据“内错角相等，两直线平行”，所以EF∥CD.又因为AB∥CD，根据“平行于同一条直线的两条直线平行”，所以EF∥AB． 问题1：如图，已知直线a∥b，直线c∥d，∠1=107°，求∠2，∠3的度数. 解：因为a∥b，根据“两直线平行，内错角相等”，所以∠2=∠1=107°.因为c∥d，根据“两直线平行，同旁内角互补”，所以∠1＋∠3=180°，所以∠3=180°-∠1=180°-107°=73°. 【规律总结】解决已知两直线平行,求角的关系的问题的基本思路(1)直接法：找图中的同位角、内错角、同旁内角,进而判断它们的关系.(2)间接法：如果没有上述角,通过添加辅助线,构造平行线,得三类角,进而求解. 1.如图，已知AB∥CD，∠A＝70°，则∠1的度数是()(A)70°(B)100°(C)110°(D)130°【解析】选C.因为AB∥CD，∠A＝70°，所以∠1的邻补角为70°,所以∠1=110°. 2.如图，已知a∥b，∠1=65°，则∠2的度数为()(A)65°(B)125°(C)115°(D)25°【解析】选C.因为a∥b，所以∠1=∠3=65°，所以∠2=180°-65°=115°. 3.如图，已知AB∥CD，∠1=70°，则∠2=______，∠3=______，∠4=______.【解析】∠2＝∠1=70°(对顶角相等)，∠3=∠1=70°(两直线平行，同位角相等).因为∠3+∠4=180°(补角的定义)，所以∠4=110°.答案：70°70°110° 4.已知AB∥CD，BE平分∠ABC，∠CDE＝150°，则∠C＝______.【解析】因为∠CDE＝150°,所以∠CDB=30°,因为AB∥CD，BE平分∠ABC，所以∠CBD=∠ABD=∠CDB=30°，所以∠ABC=60°，所以∠C＝120°.答案：120° 5.已知：AB∥CD，AE平分∠BAC，CE平分∠ACD，请说明：AE⊥CE. 【解析】过E作EM∥AB交AC于M.因为AB∥CD，则AB∥EM∥CD，所以∠BAC+∠ACD＝180°(两直线平行，同旁内角互补)，∠EAB＝∠AEM，∠ECD＝∠MEC(两直线平行，内错角相等).又因为AE平分∠BAC，CE平分∠ACD，所以∠EAC＝∠BAC，∠ECA＝∠ACD，所以∠EAC+∠ECA=(∠BAC+∠ACD)=90°,所以∠MEC+∠MEA＝180°-90°=90°，即∠AEC=90°,所以AE⊥CE. 谢谢！