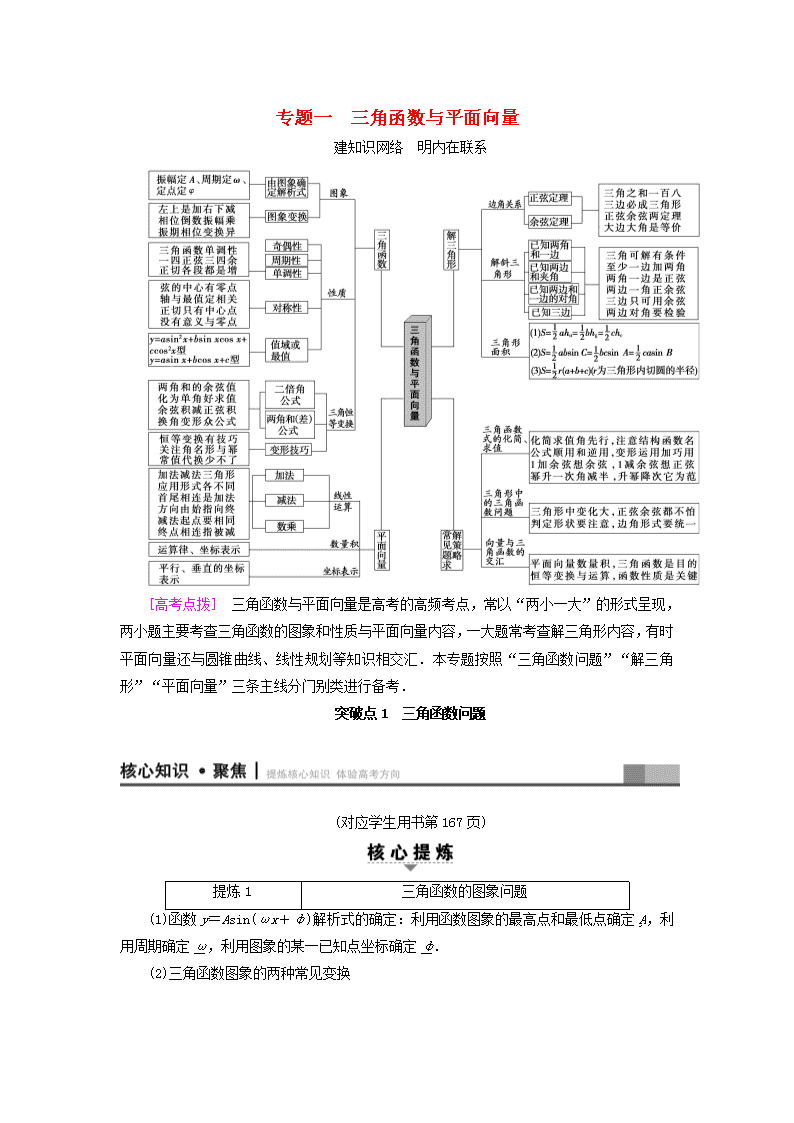
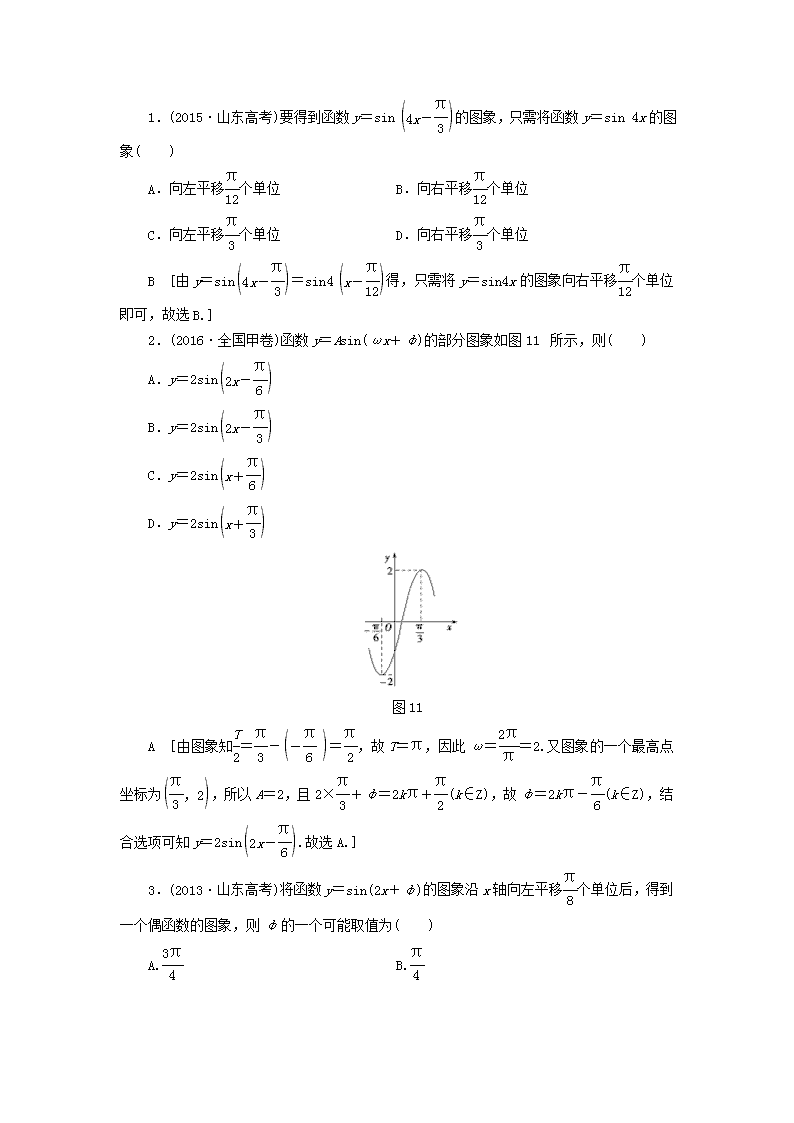高考数学二轮专题复习与策略第1部分专题1三角函数与平面向量突破点1三角函数问题教师用书理
专题一 三角函数与平面向量
建知识网络 明内在联系
[高考点拨] 三角函数与平面向量是高考的高频考点,常以“两小一大”的形式呈现,
两小题主要考查三角函数的图象和性质与平面向量内容,一大题常考查解三角形内容,有时
平面向量还与圆锥曲线、线性规划等知识相交汇.本专题按照“三角函数问题”“解三角
形”“平面向量”三条主线分门别类进行备考.
突破点 1 三角函数问题
(对应学生用书第 167 页)
提炼 1 三角函数的图象问题
(1)函数 y=Asin(ωx+φ)解析式的确定:利用函数图象的最高点和最低点确定 A,利
用周期确定ω,利用图象的某一已知点坐标确定φ.
(2)三角函数图象的两种常见变换
提炼 2 三角函数奇偶性与对称性
(1)y=Asin(ωx+φ),当φ=kπ(k∈Z)时为奇函数;当φ=kπ+π
2
(k∈Z)时为偶函
数;对称轴方程可由ωx+φ=kπ+π
2
(k∈Z)求得,对称中心的横坐标可由ωx+φ=kπ,
(k∈Z)解得.
(2)y=Acos(ωx+φ),当φ=kπ+π
2
(k∈Z)时为奇函数;当φ=kπ(k∈Z)时为偶函
数;对称轴方程可由ωx+φ=kπ(k∈Z)求得,对称中心的横坐标可由ωx+φ=kπ+π
2
(k
∈Z)解得.
y=Atan(ωx+φ),当φ=kπ(k∈Z)时为奇函数;对称中心的横坐标可由ωx+φ=
kπ
2
(k∈Z)解得,无对称轴.
提炼 3 三角变换常用技巧
(1)常值代换:特别是“1”的代换,1=sin2θ+cos2θ=tan 45°等.
(2)项的分拆与角的配凑:如 sin2α+2cos2α=(sin2α+cos2α)+cos2α,α=(α-
β)+β等.
(3)降次与升次:正用二倍角公式升次,逆用二倍角公式降次.
(4)弦、切互化:一般是切化弦.
提炼 4 三角函数最值问题
(1)y=asin x+bcos x+c 型函数的最值:可将 y 转化为 y= a2+b2sin(x+φ)+c 其
中 tan φ=b
a
的形式,这样通过引入辅助角φ可将此类函数的最值问题转化为 y=
a2+b2sin(x+φ)+c 的最值问题,然后利用三角函数的图象和性质求解.
(2)y=asin2x+bsin xcos x+ccos2x 型函数的最值:可利用降幂公式sin2x=1-cos 2x
2
,
sin xcos x=sin 2x
2
,cos2x=1+cos 2x
2
,将 y=asin2x+bsin xcos x+ccos2x 转化整理为
y=Asin 2x+Bcos 2x+C,这样就可将其转化为(1)的类型来求最值.
回访 1 三角函数的图象问题
1.(2015·山东高考)要得到函数 y=sin
4x-π
3 的图象,只需将函数 y=sin 4x 的图
象( )
A.向左平移π
12
个单位 B.向右平移π
12
个单位
C.向左平移π
3
个单位 D.向右平移π
3
个单位
B [由 y=sin
4x-π
3 =sin 4
x-π
12 得,只需将 y=sin 4x 的图象向右平移π
12
个单
位即可,故选 B.]
2.(2016·全国甲卷)函数 y=Asin(ωx+φ)的部分图象如图 11 所示,则( )
A.y=2sin
2x-π
6
B.y=2sin
2x-π
3
C.y=2sin
x+π
6
D.y=2sin
x+π
3
图 11
A [由图象知T
2
=π
3
-
-π
6 =π
2
,故 T=π,因此ω=2π
π
=2.又图象的一个最高点坐
标为
π
3
,2
,所以 A=2,且 2×π
3
+φ=2kπ+π
2
(k∈Z),故φ=2kπ-π
6
(k∈Z),结合
选项可知 y=2sin
2x-π
6 .故选 A.]
3.(2013·山东高考)将函数 y=sin(2x+φ)的图象沿 x 轴向左平移π
8
个单位后,得到
一个偶函数的图象,则φ的一个可能取值为( )
A.3π
4
B.π
4
C.0 D.-π
4
B [y=sin(2x+φ) ――→
向左平移
π
8
个单位
y=sin 2
x+π
8 +φ =sin
2x+π
4
+φ
.
当φ=3π
4
时,y=sin(2x+π)=-sin 2x,为奇函数;
当φ=π
4
时,y=sin
2x+π
2 =cos 2x,为偶函数;
当φ=0 时,y=sin
2x+π
4 ,为非奇非偶函数;
当φ=-π
4
时,y=sin 2x,为奇函数.故选 B.]
回访 2 三角函数的性质问题
4.(2016·山东高考)函数 f(x)=( 3sin x+cos x)( 3cos x-sin x)的最小正周期
是( )
A.π
2
B.π
C.3π
2
D.2π
B [法一:∵f(x)=( 3sin x+cos x)( 3cos x-sin x)
=4
3
2
sin x+1
2
cos x 3
2
cos x-1
2
sin x
=4sin
x+π
6 cos
x+π
6 =2sin
2x+π
3 ,
∴T=2π
2
=π.
法二:∵f(x)=( 3sin x+cos x)( 3cos x-sin x)
=3sin xcos x+ 3cos2x- 3sin2x-sin xcos x
=sin 2x+ 3cos 2x
=2sin
2x+π
3 ,
∴T=2π
2
=π.故选 B.]
5.(2016·全国甲卷)若将函数 y=2sin 2x 的图象向左平移π
12
个单位长度,则平移后图
象的对称轴为( )
A.x=kπ
2
-π
6
(k∈Z) B.x=kπ
2
+π
6
(k∈Z)
C.x=kπ
2
-π
12
(k∈Z) D.x=kπ
2
+π
12
(k∈Z)
B [将函数 y=2sin 2x 的图象向左平移π
12
个单位长度,得到函数 y=2sin 2
x+π
12 =
2sin
2x+π
6 的图象.由 2x+π
6
=kx+π
2
(k∈Z),得 x=kπ
2
+π
6
(k∈Z),即平移后图象的
对称轴为 x=kπ
2
+π
6
(k∈Z).]
6.(2015·全国卷Ⅰ)函数 f(x)=cos(ωx+φ)的部分图象如图 12 所示,则 f(x)的单
调递减区间为( )
图 12
A.
kπ-1
4
,kπ+3
4 ,k∈Z
B.
2kπ-1
4
,2kπ+3
4 ,k∈Z
C.
k-1
4
,k+3
4 ,k∈Z
D.
2k-1
4
,2k+3
4 ,k∈Z
D [由图象知,周期 T=2
5
4
-1
4 =2,
∴2π
ω
=2,∴ω=π.
由π×1
4
+φ=π
2
+2kπ,k∈Z,不妨取φ=π
4
,
∴f(x)=cos
πx+π
4 .
由 2kπ<πx+π
4
<2kπ+π,k∈Z,得 2k-1
4
0),则 A=________,
b=________.
2 1 [∵2cos2x+sin 2x=1+cos 2x+sin 2x=1+ 2sin
2x+π
4 ,
∴1+ 2sin
2x+π
4 =Asin(ωx+φ)+b,∴A= 2,b=1.]
(对应学生用书第 167 页)
热点题型 1 三角函数的图象问题
题型分析:高考对该热点的考查方式主要体现在以下两方面:一是考查三角函数解析式
的求法;二是考查三角函数图象的平移变换,常以选择、填空题的形式考查,难度较低.
(1)(2016·青岛模拟)将函数 y= 3cos x+sin x(x∈R)的图象向左平移 m(m
>0)个单位长度后,所得到的图象关于 y 轴对称,则 m 的最小值是( )
A.π
6
B.π
12
C.π
3
D.5π
6
(2)(2016·衡水中学四调)已知 A,B,C,D 是函数 y=sin(ωx+φ)
ω>0,0<φ<π
2
一个周期内的图象上的四个点,如图 13 所示,A
-π
6
,0
,B 为 y 轴上的点,C 为图象上
的最低点,E为该图象的一个对称中心,B与D关于点E对称,CD
→
在x轴上的投影为π
12
,则( )
图 13
A.ω=2,φ=π
3
B.ω=2,φ=π
6
C.ω=1
2
,φ=π
3
D.ω=1
2
,φ=π
6
(1)A (2)A [(1)设 f(x)= 3cos x+sin x=2
3
2
cos x+1
2
sin x
=2sin
π
3
+x
,向
左平移 m 个单位长度得 g(x)=2sin
x+m+π
3 .∵g(x)的图象关于 y 轴对称,∴g(x)为偶函
数,∴π
3
+m=π
2
+kπ(k∈Z),∴m=π
6
+kπ(k∈Z),又 m>0,∴m 的最小值为π
6
.
(2)由题意可知T
4
=π
6
+π
12
=π
4
,∴T=π,ω=2π
π
=2.又 sin 2×
-π
6 +φ =0,0<
φ<π
2
,∴φ=π
3
,故选 A.]
1.函数 y=Asin(ωx+φ)的解析式的确定
(1)A 由最值确定,A=最大值-最小值
2
;
(2)ω由周期确定;
(3)φ由图象上的特殊点确定.
提醒:根据“五点法”中的零点求φ时,一般先依据图象的升降分清零点的类型.
2.在图象变换过程中务必分清是先相位变换,还是先周期变换.变换只是相对于其中
的自变量 x 而言的,如果 x 的系数不是 1,就要把这个系数提取后再确定变换的单位长度和
方向.
[变式训练 1] (1)(2016·烟台模拟)将 f(x)=sin 2x 的图象右移φ
0<φ<π
2 个单
位后,得到 g(x)的图象,若对于满足|f(x1)-g(x2)|=2 的 x1,x2,有|x1-x2|的最小值为π
3
,
则φ的值为( )
A.π
12
B.π
6
C.π
4
D.π
3
(2)(2016·江西八校联考)函数 f(x)=Asin ωx(A>0,ω>0)的部分图象如图 14 所
示,则 f(1)+f(2)+f(3)+…+f(2 016)的值为( )
图 14
A.0 B.3 2
C.6 2 D.- 2
(1)B (2)A [(1)g(x)=sin[2(x-φ)]=sin(2x-2φ),则 f(x),g(x)的最小正周期
都是 T=π.若对满足|f(x1)-g(x2)|=2 的 x1,x2,则|x1-x2|=T
2
-φ=π
2
-φ=π
3
,从而
φ=π
6
.
(2)由题图可得,A=2,T=8,2π
ω
=8,ω=π
4
,
∴f(x)=2sinπ
4
x.
∴f(1)= 2,f(2)=2,f(3)= 2,f(4)=0,f(5)=- 2,f(6)=-2,f(7)=- 2,
f(8)=0,
而 2 016=8×252,
∴f(1)+f(2)+…+f(2 016)=0.]
热点题型 2 三角函数的性质问题
题型分析:三角函数的性质涉及周期性、单调性以及最值、对称性等,是高考的重要命
题点之一,常与三角恒等变换交汇命题,难度中等.
(2016·天津高考)已知函数 f(x)=4tan x·sin
π
2
-x
·cos
x-π
3 - 3.
(1)求 f(x)的定义域与最小正周期;
(2)讨论 f(x)在区间
-π
4
,π
4 上的单调性.
[解] (1)f(x)的定义域为 x|x≠π
2
+kπ,k∈Z
.1 分
f(x)=4tan xcos xcos
x-π
3 - 3
=4sin xcos
x-π
3 - 3
=4sin x
1
2
cos x+ 3
2
sin x
- 3
=2sin xcos x+2 3sin2x- 3
=sin 2x+ 3(1-cos 2x)- 3
=sin 2x- 3cos 2x=2sin
2x-π
3 .4 分
所以 f(x)的最小正周期 T=2π
2
=π.6 分
(2)令 z=2x-π
3
,则函数 y=2sin z 的单调递增区间是
-π
2
+2kπ,π
2
+2kπ
,k∈
Z.
由-π
2
+2kπ≤2x-π
3
≤π
2
+2kπ,
得-π
12
+kπ≤x≤5π
12
+kπ,k∈Z.8 分
设 A=
-π
4
,π
4 ,B=x-π
12
+kπ≤x≤5π
12
+kπ,k∈Z,易知 A∩B=
-π
12
,π
4 .10
分
所以当 x∈
-π
4
,π
4 时,f(x)在区间
-π
12
,π
4 上单调递增,在区间
-π
4
,-π
12 上
单调递减.12 分
研究函数 y=Asin(ωx+φ)的性质的“两种”意识
1.转化意识:利用三角恒等变换把待求函数化成 y=Asin(ωx+φ)+B 的形式.
2.整体意识:类比于研究 y=sin x 的性质,只需将 y=Asin(ωx+φ)中的“ωx+φ”
看成 y=sin x 中的“x”代入求解便可.
[变式训练 2] (1)(2016·济宁模拟)已知函数 f(x)=2sin
2x+π
6 ,把函数 f(x)的图
象沿 x 轴向左平移π
6
个单位,得到函数 g(x)的图象.关于函数 g(x),下列说法正确的是
( )
A.在
π
4
,π
2 上是增函数
B.其图象关于直线 x=-π
4
对称
C.函数 g(x)是奇函数
D.当 x∈
π
6
,2
3
π
时,函数 g(x)的值域是[-2,1]
(2)已知函数 f(x)=-2sin(2x+φ)(|φ|<π),若
π
5
,5π
8 是 f(x)的一个单调递增
区间,则φ的取值范围为( ) 【导学号:67722009】
A.
-3π
10
,-9π
10
B.
9π
10
,4π
4
C.
π
10
,π
4
D.
-∞,π
10 ∪
3π
4
,+∞
(1)D (2)C [(1)因为 f(x)=2sin
2x+π
6 ,把函数 f(x)的图象沿 x 轴向左平移π
6
个
单位,得 g(x)=f
x+π
6 =2sin 2
x+π
6 +π
6 =2sin
2x+π
2 =2cos 2x.
对于 A,由 x∈
π
4
,π
2 可知 2x∈
π
2
,π
,故 g(x)在
π
4
,π
2 上是减函数,故 A 错;
又 g
-π
4 =2cos
-π
2 =0,故 x=-π
4
不是 g(x)的对称轴,故 B 错;又 g(-x)=2cos 2x
=g(x),故 C 错;又当 x∈
π
6
,2π
3 时,2x∈
π
3
,4π
3 ,故 g(x)的值域为[-2,1],D 正确.
(2)令 2kπ+π
2
<2x+φ<2kπ+3π
2
,k∈Z,
所以 kπ+π
4
-φ
2
≤x≤kπ+3π
4
-φ
2
,k∈Z,
所以函数 f(x)在
kπ+π
4
-φ
2
,kπ+3π
4
-φ
2 上单调递增.
因为
π
5
,5π
8 是 f(x)的一个单调递增区间,
所以5π
8
≤kπ+3π
4
-φ
2
,且 kπ+π
4
-φ
2
≤π
5
,k∈Z,
解得 2kπ+π
10
≤φ≤2kπ+π
4
,k∈Z,又|φ|<π,所以π
10
≤φ≤π
4
.故选 C.]
热点题型 3 三角恒等变换
题型分析:高考对该热点的考查方式主要体现在以下两个方面:一是直接利用和、差、
倍、半角公式对三角函数式化简求值;二是以三角恒等变换为载体,考查 y=Asin ωx+
φ 的有关性质.
(1)(2016·江西八校联考)如图 15,圆 O 与 x 轴的正半轴的交点为 A,点 C,B
在圆 O 上,且点 C 位于第一象限,点 B 的坐标为
12
13
,- 5
13 ,∠AOC=α,若|BC|=1,则
3cos2α
2
-sinα
2
cos α
2
- 3
2
的值为________.
图 15
(2)已知函数 f(x)=sin25x
6
-cos25x
6
+2 3sin5x
6
·cos5x
6
+λ的图象经过点
π
4
,0
,则
函数 f(x)在区间
0,3π
10 上的最大值为________.
(1) 5
13
(2) 3- 2 [(1)由题意可知|OB|=|BC|=1,∴△OBC 为正三角形.
由三角函数的定义可知,sin∠AOB=sin
π
3
-α
= 5
13
,
∴ 3cos2α
2
-sinα
2
cosα
2
- 3
2
= 3 1+cos α
2
-sin α
2
- 3
2
= 3
2
cos α-1
2
sin α
=sin
π
3
-α
= 5
13
.
(2)f(x)=sin2 5x
6
-cos2 5x
6
+2 3sin5x
6
·cos 5x
6
+λ=-cos5x
3
+ 3sin5x
3
+λ=
2sin
5x
3
-π
6 +λ.
由 f(x)的图象过点
π
4
,0
,得λ=-2sin
5
3
×π
4
-π
6 =-2sinπ
4
=- 2,
故 f(x)=2sin
5
3
x-π
6 - 2.
因为 0≤x≤3π
10
,所以-π
6
≤5x
3
-π
6
≤π
3
.
因为 y=sin x 在
-π
6
,π
3 上单调递增,
所以 f(x)的最大值为 f
3π
10 =2sinπ
3
- 2= 3- 2.]
1.解决三角函数式的化简求值要坚持“三看”原则:一看“角”,通过看角之间的差
别与联系,把角进行合理的拆分;二是“函数名称”,是需进行“切化弦”还是“弦化切”
等,从而确定使用的公式;三看“结构特征”,了解变式或化简的方向.
2.在研究形如 f(x)=asin ωx+bcos ωx 的函数的性质时,通常利用辅助角公式 asin
x+bcos x= a2+b2·sin(x+φ)把函数 f(x)化为 Asin(ωx+φ)的形式,通过对函数 y=
Asin(ωx+φ)性质的研究得到 f(x)=asin ωx+bcos ωx 的性质.
[变式训练 3] (1)(2014·全国卷Ⅰ)设α∈
0,π
2 ,β∈
0,π
2 ,且 tan α=
1+sin β
cos β
,则( )
A.3α-β=π
2
B.2α-β=π
2
C.3α+β=π
2
D.2α+β=π
2
(2)已知 sin
α+π
3 +sin α=-4 3
5
,-π
2
<α<0,则 cos
α+2π
3 等于( )
A.-4
5
B.-3
5
C.4
5
D.3
5
(1)B (2)C [(1)法一:由 tan α=1+sin β
cos β
得sin α
cos α
=1+sin β
cos β
,
即 sin αcos β=cos α+cos αsin β,
∴sin(α-β)=cos α=sin
π
2
-α
.
∵α∈
0,π
2 ,β∈
0,π
2 ,
∴α-β∈
-π
2
,π
2 ,π
2
-α∈
0,π
2 ,
由 sin(α-β)=sin
π
2
-α
,得α-β=π
2
-α,
∴2α-β=π
2
.
法二:tan α=1+sin β
cos β
=
1+cos
π
2
-β
sin
π
2
-β
=
2cos2
π
4
-β
2
2sin
π
4
-β
2 cos
π
4
-β
2
=cot
π
4
-β
2
=tan
π
2
-
π
4
-β
2
=tan
π
4
+β
2 ,
∴α=kπ+
π
4
+β
2 ,k∈Z,
∴2α-β=2kπ+π
2
,k∈Z.
当 k=0 时,满足 2α-β=π
2
,故选 B.
(2)∵sin
α+π
3 +sin α=-4 3
5
,-π
2
<α<0,
∴3
2
sin α+ 3
2
cos α=-4 3
5
,
∴ 3
2
sin α+1
2
cos α=-4
5
,
∴cos
α+2π
3 =cos αcos 2π
3
-sin αsin 2π
3
=-1
2
cos α- 3
2
sin α=4
5
.]
专题一 三角函数与平面向量
建知识网络 明内在联系
[高考点拨] 三角函数与平面向量是高考的高频考点,常以“两小一大”的形式呈现,
两小题主要考查三角函数的图象和性质与平面向量内容,一大题常考查解三角形内容,有时
平面向量还与圆锥曲线、线性规划等知识相交汇.本专题按照“三角函数问题”“解三角
形”“平面向量”三条主线分门别类进行备考.
专题限时集训(一) 三角函数问题
[建议 A、B 组各用时:45 分钟]
[A 组 高考达标]
一、选择题
1.(2016·泰安模拟)函数 f(x)=sin(2x+φ)
|φ|<π
2 的图象向左平移π
6
个单位后
关于原点对称,则函数 f(x)在
0,π
2 上的最小值为( ) 【导学号:67722010】
A.- 3
2
B.-1
2
C.1
2
D. 3
2
A [函数 f(x)=sin(2x+φ)向左平移π
6
个单位得 y=sin 2
x+π
6 +φ =sin
2x+π
3
+φ
,又其为奇函数,故π
3
+φ=kπ,π∈Z,解得φ=kπ-π
3
,又|φ|<π
2
,
令 k=0,得φ=-π
3
,
∴f(x)=sin
2x-π
3 .
又∵x∈
0,π
2 ,
∴2x-π
3
∈
-π
3
,2
3
π
,∴sin
2x-π
3 ∈
- 3
2
,1
,
当 x=0 时,f(x)min=- 3
2
,故选 A.]
2.(2016·河南八市联考)已知函数 f(x)=sin x-cos x,且 f′(x)=1
2
f(x),则 tan 2x
的值是( )
A.-2
3
B.-4
3
C.4
3
D.3
4
D [因为 f′(x)=cos x+sin x=1
2
sin x-1
2
cos x,所以 tan x=-3,所以 tan 2x=
2tan x
1-tan2x
= -6
1-9
=3
4
,故选 D.]
3.(2016·全国甲卷)函数 f(x)=cos 2x+6cos
π
2
-x
的最大值为( )
A.4 B.5
C.6 D.7
B [∵f(x)=cos 2x+6cos
π
2
-x
=cos 2x+6sin x
=1-2sin2x+6sin x=-2
sin x-3
2 2+11
2
,
又 sin x∈[-1,1],∴当 sin x=1 时,f(x)取得最大值 5.故选 B.]
4.(2016·郑州模拟)函数 f(x)=2sin(ωx+φ)
ω>0,|φ|<π
2 的部分图象如图
16 所示,则 f(0)+f
17π
12 的值为( )
图 16
A.2- 3 B.2+ 3
C.1- 3
2
D.1+ 3
2
A [由函数 f(x)的图象得函数 f(x)的最小正周期为 T=2π
ω
=4
π
6
-
-π
12 =π,解得
ω=2,则 f(x)=2sin(2x+φ).又因为函数图象经过点-π
12
,-2,所以 f-π
12
=
2sin 2×
-π
12 +φ =-2,则 2×
-π
12 +φ=-π
2
+2kπ,k∈Z,解得φ=-π
3
+2kπ,
k∈Z.又因为|φ|<π
2
,所以φ=-π
3
,则 f(x)=2sin
2x-π
3 ,所以 f(0)+f
17π
12 =
2sin
2×0-π
3 +2sin
2×17π
12
-π
3 =2sin
-π
3 +2sin5π
2
=- 3+2,故选 A.]
5.(2016·石家庄二模)设α,β∈[0,π],且满足 sin αcos β-cos αsin β=1,
则 sin(2α-β)+sin(α-2β)的取值范围为( )
A.[-1,1] B.[-1, 2]
C.[- 2,1] D.[1, 2]
A [由 sin αcos β-cos αsin β=sin(α-β)=1,α,β∈[0,π],得α-β
=π
2
,β=α-π
2
∈[0,π]⇒α∈
π
2
,π
,且 sin(2α-β)+sin(α-2β)=sin
α+π
2
+sin(π-α)=cos α+sin α= 2sin
α+π
4 ,α∈
π
2
,π
⇒α+π
4
∈
3π
4
,5π
4 ⇒
sin
α+π
4 ∈
- 2
2
, 2
2 ⇒ 2sin
α+π
4 ∈[-1,1],故选 A.]
二、填空题
6.(2016·合肥三模)已知 tan α=2,则 sin2
π
2
+α
-sin(3π+α)cos(2π-α)
=________. 【导学号:67722011】
3
5
[∵tan α=2,
∴sin2
π
2
+α
-sin(3π+α)cos(2π-α)
=cos2α+sin αcos α
=cos2α+sin αcos α
sin2α+cos2α
=1+tan α
tan2α+1
=1+2
4+1
=3
5
.]
7.(2016·兰州模拟)已知函数 f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)为奇函
数,该函数的部分图象如图 17 所示,△EFG(点 G 在图象的最高点)是边长为 2 的等边三角
形,则 f(1)=________.
图 17
- 3 [由函数 f(x)=Acos(ωx+φ)(A>0,ω>0,0<φ<π)是奇函数可得φ=π
2
,
则 f(x)=Acos
ωx+π
2 =-Asin ωx(A>0,ω>0).又由△EFG 是边长为 2 的等边三角形
可得 A= 3,最小正周期 T=4=2π
ω
,ω=π
2
,则 f(x)=- 3sinπ
2
x,f(1)=- 3.]
8.(2015·天津高考)已知函数 f(x)=sin ωx+cos ωx(ω>0),x∈R.若函数 f(x)在
区间(-ω,ω)内单调递增,且函数 y=f(x)的图象关于直线 x=ω对称,则ω的值为
________.
π
2
[f(x)=sin ωx+cos ωx= 2sinωx+π
4
,
因为 f(x)在区间(-ω,ω)内单调递增,且函数图象关于直线 x=ω对称,
所以 f(ω)必为一个周期上的最大值,所以有ω·ω+π
4
=2kπ+π
2
,k∈Z,
所以ω2=π
4
+2kπ,k∈Z.
又ω-(-ω)≤
2π
ω
2
,即ω2≤π
2
,所以ω2=π
4
,
所以ω= π
2
.]
三、解答题
9.(2016·临沂高三模拟)已知函数 f(x)=Asin(ωx+φ)
A>0,ω>0,|φ|<π
2 满
足下列条件:
①周期 T=π;②图象向左平移π
6
个单位长度后关于 y 轴对称;③f(0)=1.
(1)求函数 f(x)的解析式;
(2)设α,β∈
0,π
4 ,f
α-π
3 =-10
13
,f
β+π
6 =6
5
,求 cos(2α-2β)的值.
[解] (1)f(x)的周期 T=π,∴ω=2.1 分
f(x)的图象向左平移π
6
个单位长度,变为 g(x)=Asin 2
x+π
6 +φ .2 分
由题意,g(x)关于 y 轴对称,
∴2×π
6
+φ=π
2
+kπ,k∈Z.3 分
又|φ|<π
2
,∴φ=π
6
,∴f(x)=Asin
2x+π
6 .4 分
∵f(0)=1,∴Asinπ
6
=1,∴A=2.5 分
因此,f(x)=2sin
2x+π
6 .6 分
(2)由 f
α-π
3 =-10
13
,f
β+π
6 =6
5
,得 2sin
2α-2π
3
+π
6 =-10
13
,
2sin
2β+π
3
+π
6 =6
5
.7 分
∵α,β∈
0,π
4 ,∴2α,2β∈
0,π
2 ,∴cos 2α= 5
13
,cos 2β=3
5
,sin 2α=
12
13
,sin 2β=4
5
,11 分
cos(2α-2β)=cos 2αcos 2β+sin 2αsin 2β
= 5
13
×3
5
+12
13
×4
5
=63
65
.12 分
10.已知函数 f(x)=Asin(ωx+φ)x∈R,A>0,ω>0,0<φ<π
2
的部分图象如图 18
所示,P 是图象的最高点,Q 为图象与 x 轴的交点,O 为坐标原点.若 OQ=4,OP= 5,PQ
= 13.
图 18
(1)求函数 y=f(x)的解析式;
(2)将函数 y=f(x)的图象向右平移 2 个单位后得到函数 y=g(x)的图象,当 x∈(-1,2)
时,求函数 h(x)=f(x)·g(x)的值域.
[解] (1)由条件知 cos ∠POQ=42+ 5 2- 13 2
2×4× 5
= 5
5
.2 分
又 cos ∠POQ= xP
5
,∴xP=1,∴yP=2,∴P(1,2).3 分
由此可得振幅 A=2,周期 T=4×(4-1)=12,又2π
ω
=12,则ω=π
6
.4 分
将点 P(1,2)代入 f(x)=2sin
π
6
x+φ
,
得 sin
π
6
+φ
=1.
∵0<φ<π
2
,∴φ=π
3
,于是 f(x)=2sin
π
6
x+π
3 .6 分
(2)由题意可得 g(x)=2sin
π
6
x-2 +π
3 =2sin π
6
x.7 分
∴h(x)=f(x)·g(x)=4sin
π
6
x+π
3 ·sin π
6
x
=2sin2π
6
x+2 3sin π
6
x·cos π
6
x
=1-cos π
3
x+ 3sin π
3
x=1+2sin
π
3
x-π
6 .9 分
当 x∈(-1,2)时,π
3
x-π
6
∈
-π
2
,π
2 ,10 分
∴sin
π
3
x-π
6 ∈(-1,1),
即 1+2sin
π
3
x-π
6 ∈(-1,3),于是函数 h(x)的值域为(-1,3).12 分
[B 组 名校冲刺]
一、选择题
1.已知函数 y=loga(x-1)+3(a>0,且 a≠1)的图象恒过定点 P,若角α的顶点与原
点重合,始边与 x 轴的正半轴重合,终边经过点 P,则 sin2α-sin 2α的值为( )
A. 5
13
B.- 5
13
C. 3
13
D.- 3
13
D [根据已知可得点 P 的坐标为(2,3),根据三角函数定义,可得 sin α= 3
13
,cos α
= 2
13
,所以 sin2α-sin 2α=sin2α-2sin αcos α=
3
13 2-2× 3
13
× 2
13
=- 3
13
.]
2.(2016·东北三省四市第二次联考)将函数 f(x)=sin(2x+φ)
|φ|<π
2 的图象向
右平移π
12
个单位,所得到的图象关于 y 轴对称,则函数 f(x)在
0,π
2 上的最小值为( )
A. 3
2
B.1
2
C.-1
2
D.- 3
2
D [f(x)=sin(2x+φ)向右平移π
12
个单位得到函数 g(x)=sin 2
x-π
12 +φ =sin2x
-π
6
+φ,此函数图象关于 y 轴对称,即函数 g(x)为偶函数,则-π
6
+φ=π
2
+kπ,k∈Z.
又|φ|<π
2
,所以φ=-π
3
,所以 f(x)=sin
2x-π
3 .因为 0≤x≤π
2
,所以-π
3
≤2x-
π
3
≤2π
3
,所以 f(x)的最小值为 sin
-π
3 =- 3
2
,故选 D.]
3.(2016·湖北七市四月联考)已知函数 f(x)=asin x-bcos x(a,b 为常数,a≠0,x
∈R)在 x=π
4
处取得最大值,则函数 y=f
x+π
4 是( )
A.奇函数且它的图象关于点(π,0)对称
B.偶函数且它的图象关于点
3π
2
,0
对称
C.奇函数且它的图象关于点
3π
2
,0
对称
D.偶函数且它的图象关于点(π,0)对称
B [由题意可知 f′
π
4 =0,
即 acosπ
4
+bsinπ
4
=0,∴a+b=0,
∴f(x)=a(sin x+cos x)= 2asin
x+π
4 .
∴f
x+π
4 = 2asin
x+π
2 = 2acos x.
易知 f
x+π
4 是偶函数且图象关于点
3π
2
,0
对称,故选 B.]
4.(2016·陕西省第二次联考)已知函数 f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
π)的部分图象如图 19 所示,且 f(α)=1,α∈
0,π
3 ,则 cos
2α+5π
6 =( )
图 19
A.±2 2
3
B.2 2
3
C.-2 2
3
D.1
3
C [由图易得 A=3,函数 f(x)的最小正周期 T=2π
ω
=4×
7π
12
-π
3 ,解得ω=2,所
以 f(x)=3sin(2x+φ).又因为点
π
3
,-3
在函数图象上,所以 f
π
3 =3sin
2×π
3
+φ
=
-3,解得 2×π
3
+φ=3
2
π+2kπ,k∈Z,解得φ=5π
6
+2kπ,k∈Z.又因为 0<φ<π,
所以φ=5π
6
,则 f(x)=3sin
2x+5π
6 ,当α∈
0,π
3 时,2α+5π
6
∈
5π
6
,3π
2 .又因为
f(α)=3sin
2α+5π
6 =1,所以 sin
2α+5π
6 =1
3
>0,所以 2α+5π
6
∈
5π
6
,π
,则
cos
2α+5π
6 =- 1-sin2 2α+5π
6 =-2 2
3
,故选 C.]
二、填空题
5.已知函数 f(x)=sin ωx+cos ωx(ω>0)在
π
2
,π
上单调递减,则ω的取值范
围是________.
【导学号:67722012】
1
2
,5
4 [f(x)=sin ωx+cos ωx= 2sinωx+π
4
,令 2kπ+π
2
≤ωx+π
4
≤2kπ+
3π
2
(k∈Z),解得2kπ
ω
+ π
4ω
≤x≤2kπ
ω
+5π
4ω
(k∈Z).
由题意,函数 f(x)在
π
2
,π
上单调递减,故
π
2
,π
为函数单调递减区间的一个子区
间,故有
2kπ
ω
+ π
4ω
≤π
2
,
2kπ
ω
+5π
4ω
≥π,
解得 4k+1
2
≤ω≤2k+5
4
(k∈Z).
由 4k+1
2
<2k+5
4
,解得 k<3
8
.
由ω>0,可知 k≥0,
因为 k∈Z,所以 k=0,故ω的取值范围为
1
2
,5
4 .]
6.设函数 f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0).若 f(x)在区间
π
6
,π
2
上具有单调性,且 f
π
2 =f
2π
3 =-f
π
6 ,则 f(x)的最小正周期为________.
π [∵f(x)在
π
6
,π
2 上具有单调性,
∴T
2
≥π
2
-π
6
,∴T≥2π
3
.
∵f
π
2 =f
2π
3 ,
∴f(x)的一条对称轴为 x=
π
2
+2π
3
2
=7π
12
.
又∵f
π
2 =-f
π
6 ,
∴f(x)的一个对称中心的横坐标为
π
2
+π
6
2
=π
3
,
∴1
4
T=7π
12
-π
3
=π
4
,∴T=π.]
三、解答题
7 . (2015· 湖 北 高 考 ) 某 同 学 用 “ 五 点 法 ” 画 函 数 f(x) = Asin(ωx +
φ)
ω>0,|φ|<π
2 在某一个周期内的图象时,列表并填入了部分数据,如下表:
ωx+φ 0 π
2 π 3π
2 2π
x π
3
5π
6
Asin(ωx+φ) 0 5 -5 0
(1)请将上表数据补充完整,并直接写出函数 f(x)的解析式;
(2)将 y=f(x)图象上所有点向左平行移动θ(θ>0)个单位长度,得到 y=g(x)的图
象.若 y=g(x)图象的一个对称中心为
5π
12
,0
,求θ的最小值.
[解] (1)根据表中已知数据,解得 A=5,ω=2,φ=-π
6
,数据补全如下表:
ωx+φ 0 π
2 π 3π
2 2π
x π
12
π
3
7π
12
5π
6
13
12
π
Asin(ωx+φ) 0 5 0 -5 0
4 分
且函数解析式为 f(x)=5sin
2x-π
6 .6 分
(2)由(1)知 f(x)=5sin
2x-π
6 ,
则 g(x)=5sin
2x+2θ-π
6 .7 分
因为函数 y=sin x 图象的对称中心为(kπ,0),k∈Z,
令 2x+2θ-π
6
=kπ,解得 x=kπ
2
+π
12
-θ,k∈Z.8 分
由于函数 y=g(x)的图象关于点
5π
12
,0
成中心对称,
所以令kπ
2
+π
12
-θ=5π
12
,
解得θ=kπ
2
-π
3
,k∈Z.10 分
由θ>0 可知,当 k=1 时,θ取得最小值π
6
.12 分
8.(2016·潍坊模拟)已知函数 f(x)=2 3sin xcos x-sin2x+1
2
cos 2x+1
2
,x∈R.
(1)求函数 f(x)在
-π
4
,π
2 上的最值;
(2)若将函数 f(x)的图象向右平移π
4
个单位,再将得到的图象上各点横坐标伸长到原来
的 2 倍,纵坐标不变,得到 g(x)的图象.已知 g(α)=-6
5
,α∈
4π
3
,11π
6 ,求 cos
α
2
-π
6
的值.
[解] (1)f(x)=2 3sin xcos x-sin2x+1
2
cos 2x+1
2
= 3sin 2x-1-cos 2x
2
+1
2
cos 2x+1
2
= 3sin 2x+cos 2x=2sin
2x+π
6 .2 分
∵-π
4
≤x≤π
2
,∴-π
3
≤2x+π
6
≤7π
6
,3 分
∴当 2x+π
6
=-π
3
,即 x=-π
4
时,f(x)的最小值为 2×
- 3
2 =- 3.4 分
当 2x+π
6
=π
2
,即 x=π
6
时,f(x)的最大值为 2×1=2.5 分
(2)若将函数 f(x)的图象向右平移π
4
个单位,再将得到的图象上各点横坐标伸长到原来
的 2 倍,纵坐标不变,得到 g(x)=2sin
x-π
3 .7 分
由 g(α)=2sin
α-π
3 =-6
5
,得 sin
α-π
3
=-3
5
.8 分
∵4π
3
<α<11π
6
,∴π<α-π
3
<3π
2
,
∴cos
α-π
3 =-4
5
.10 分
∵π
2
<α
2
-π
6
<3π
4
,11 分
∴cos
α
2
-π
6 =- 1+cos
α-π
3
2
=-
1-4
5
2
=- 10
10
.12 分