高考数学复习课时提能演练(十六) 2_13
课时提能演练(十六)
(45分钟 100分)
一、选择题(每小题6分,共36分)
1. (2012·福州模拟)函数f(x)=x2+2x+m(x,m∈R)的最小值为-1,则f(x)dx等于( )
(A)2 (B) (C)6 (D)7
2.求曲线y=x2与y=x所围成图形的面积,其中正确的是( )
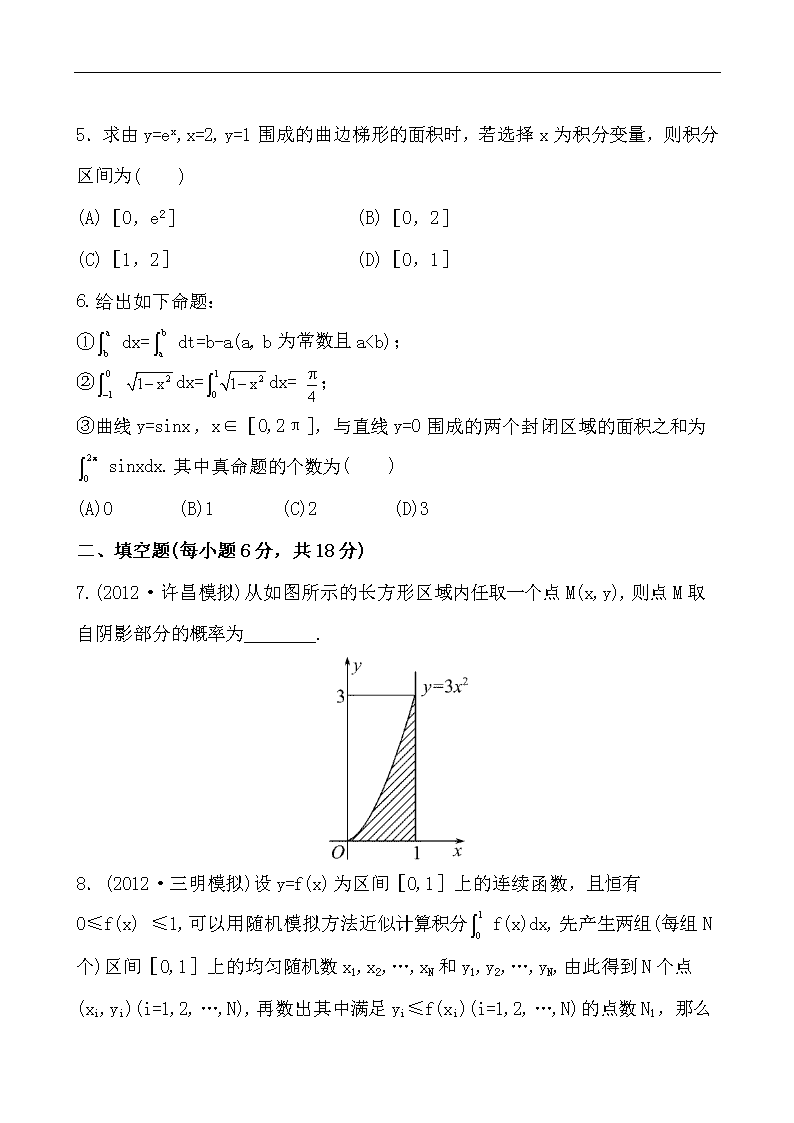
(A)S=(x2-x)dx
(B)S=(x-x2)dx
(C)S=(y2-y)dy
(D)S=(y- )dy
3.若某产品一天内的产量是时间t的函数,若已知产量的变化率为a=,那么从第3小时到第6小时期间内的产量为( )
(A) (B)3-
(C)6+3 (D)6-3
4.曲线y=sinx与直线x=0、x=、x轴所围成的图形的面积为( )
(A) (B)
(C) (D)2
5.求由y=ex,x=2,y=1围成的曲边梯形的面积时,若选择x为积分变量,则积分区间为( )
(A)[0,e2] (B)[0,2]
(C)[1,2] (D)[0,1]
6.给出如下命题:
①dx=dt=b-a(a,b为常数且a
1,若 (2x+1)dx=t2,则t=__________.
三、解答题(每小题15分,共30分)
10.(易错题)求曲线y=log2x与曲线y=log2(4-x)以及x轴所围成的图形的面积.
11.(2012·佛山模拟)已知y=ax2+bx通过点(1,2),与y=-x2+2x有一个交点,交点横坐标为x1,且a<0.如图所示:
(1)求y=ax2+bx与y=-x2+2x所围的面积S与a的函数关系.
(2)当a,b为何值时,S取得最小值.
【探究创新】
(16分)在区间[0,1]上给定曲线y=x2,如图所示,试在此区间内确定t的值,使图中的阴影部分的面积S1与S2之和最小.
答案解析
1. 【解析】选B.f(x)=x2+2x+m=(x+1)2+m-1,最小值为-1,即m-1=-1,∴m=0,
∴
2.【解题指南】根据定积分的几何意义,确定积分上、下限和被积函数.
【解析】选B.两函数图象的交点坐标是(0,0),(1,1),故积分上限是1,下限是0,由于在[0,1]上,x≥x2,故曲线y=x2与y=x所围成图形的面积S=.
3.【解析】选D.所求产量为.
4.【解析】选C.S=.
5.【解析】选B.求出y=ex,x=2,y=1的交点分别为(0,1),(2,1),(2,e2),结合定积分的几何意义知,积分区间为[0,2].
6.【解析】选B.由定积分的定义知,①不正确;由定积分的几何意义知,②正确;③中两个区域的面积大小相等,用定积分表示时互为相反数,不正确.
7.【解析】阴影部分的面积为S阴影==1,所以点M取自阴影部分的概率P= ==.
答案:
8.【解题指南】由随机模拟想到几何概型,然后结合定积分的几何意义进行求解.
【解析】
由题意可知,x,y所有取值构成的区域是一个边长为1的正方形,而满足yi≤f(xi)的点(xi,yi)落在y=f(x)、y=0以及x=1、x=0围成的区域内,由几何概型的计算公式可知的近似值为.
答案:
9.【解析】 (2x+1)dx=(x2+x)=t2+t-2=t2,
∴t=2.
答案:2
10.【解析】如图,y=log2x⇒
f(y)=x=2y,
y=log2(4-x)⇒
g(y)=x=4-2y,
所求图形的面积为
S= =
=(4y-2×2ylog2e)=4-2log2e.
【方法技巧】求由曲线围成图形的面积的一般步骤:
(1)根据题意画出图形;
(2)找出范围,确定积分上、下限;
(3)确定被积函数;
(4)将面积用定积分表示;
(5)用微积分基本定理计算定积分,求出结果.
【变式备选】求由抛物线y2=8x(y>0)与直线x+y-6=0及y=0所围成的图形的面积.
【解析】由题意,作出图形(如图所示),
解方程组得或 (舍去),
所以y2=8x(y>0)与直线x+y-6=0的交点为(2,4),
所以所求面积为S=dx+
=× +(6x-x2)
=+[(6×6-×62)-(6×2-×22)]
=+8=.
11.【解析】(1)由y=ax2+bx通过点(1,2)可得a+b=2,即b=2-a,
由y=ax2+bx与y=-x2+2x联立方程组,解得x1=.
则y=ax2+bx与y=-x2+2x所围的面积S与a的函数关系为
S=[(ax2+bx)-(-x2+2x)]dx
=[(ax2+2x-ax)-(-x2+2x)]dx
=[(a+1)x3-ax2]
=(a+1)()3-a()2=-.
(2)求导可得S′=-·
=-·=-·
由S′>0得-3
查看更多