2016年高考真题——理科数学（新课标Ⅱ）原卷版

2016年高考真题——理科数学（新课标Ⅱ）原卷版

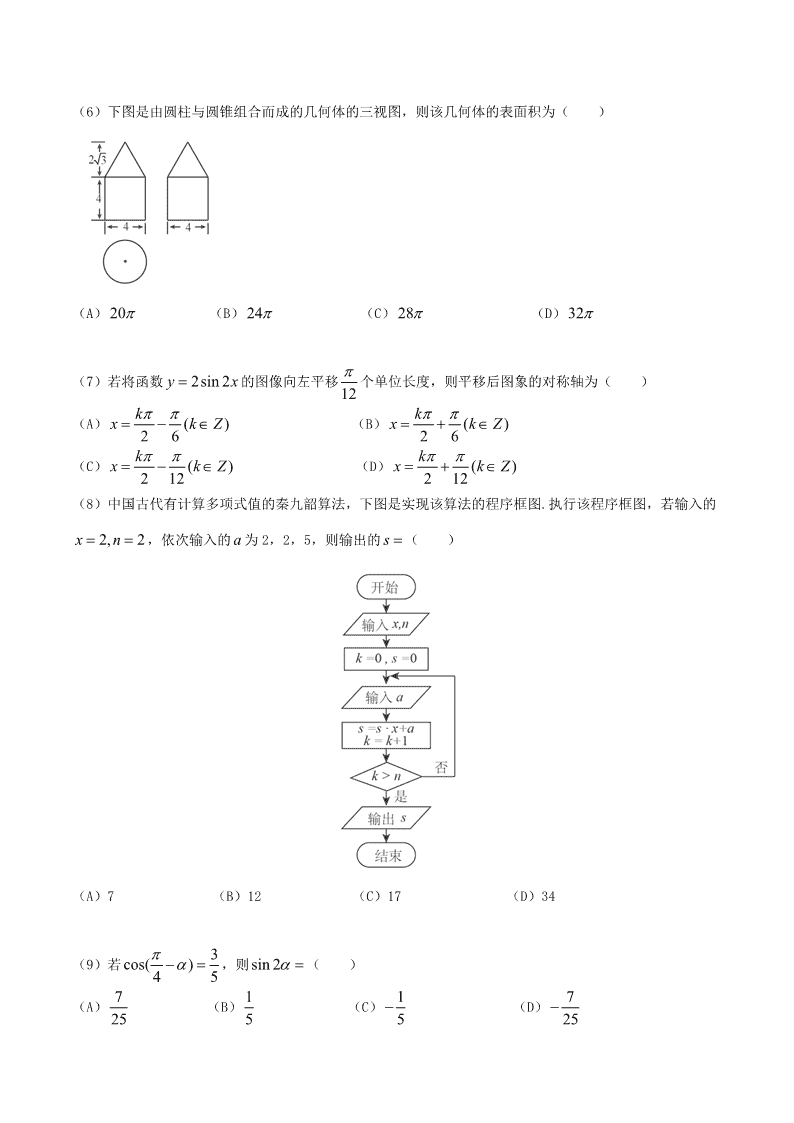
注意事项： 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷 1 至 3 页，第Ⅱ卷 3 至 5 页. 2.答题前，考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成，答在本试题上无效. 4.考试结束后，将本试题和答题卡一并交回. 第Ⅰ卷 一.选择题：本题共 12 小题，每小题 5 分，在每小题给出的四个选项中，只有一项是符合题 目要求的. （1）已知 在复平面内对应的点在第四象限，则实数 的取值范围是（ ） （A） （B） （C） （D） （2）已知集合 ， ，则 （ ） （A） （B） （C） （D） （3）已知向量 ，且 ，则 （ ） （A）－8 （B）－6 （C）6 （D）8 （4）圆 的圆心到直线 的距离为 1，则 a=（ ） （A） （B） （C） （D）2 （5）如图，小明从街道的 E 处出发，先到 F 处与小红会合，再一起到位于 G 处的老年公寓参加志愿者活动， 则小明到老年公寓可以选择的最短路径条数为（ ） （A）24 （B）18 （C）12 （D）9 ( 3) ( 1)iz m m    m ( 31) ， ( 13) ， (1, )+ ( 3) - ， {1, }A  2, 3 { | ( 1)( 2) 0, }B x x x x    Z A B  {1} {1 2}， {01 2 3}，，， { 1 01 2 3} ，，，， (1, ) (3, 2)a m a  ，= ( )a b b  + m  2 2 2 8 13 0x y x y     1 0ax y   4 3 3 4 3 （6）下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（ ） （A） （B） （C） （D） （7）若将函数 的图像向左平移 个单位长度，则平移后图象的对称轴为（ ） （A） （B） （C） （D） （8）中国古代有计算多项式值的秦九韶算法，下图是实现该算法的程序框图.执行该程序框图，若输入的 ，依次输入的 为 2，2，5，则输出的 （ ） （A）7 （B）12 （C）17 （D）34 ] （9）若 ，则 （ ） （A） （B） （C） （D） 20 24 28 32 2sin 2y x 12  ( )2 6 kx k Z    ( )2 6 kx k Z    ( )2 12 kx k Z    ( )2 12 kx k Z    2, 2x n  a s  3cos( )4 5    sin 2  7 25 1 5 1 5 7 25 （10）从区间 随机抽取 个数 , ，…， ， ， ，…， ，构成 n 个数对 ， ，…， ，其中两数的平方和小于 1 的数对共有 个，则用随机模拟的方法得到的圆周率 的近似值为 （A） （B） （C） （D） （11）已知 是双曲线 的左，右焦点，点 在 上， 与 轴垂直， ,则 的离心率为（ ） （A） （B） （C） （D）2 （12）已知函数 满足 ，若函数 与 图像的交点为 则 （ ） （A）0 （B） （C） （D） 第Ⅱ卷 本卷包括必考题和选考题两部分.第 13 ～21 题为必考题，每个试题考生都必须作答.第 22～24 题为选考题， 考生根据要求作答. 二、填空题：本大题共 3 小题，每小题 5 分 (13) 的内角 的对边分别为 ，若 ， ， ，则 ． (14) 是两个平面， 是两条直线，有下列四个命题： （1）如果 ，那么 . （2）如果 ，那么 . （3）如果 ，那么 . （4）如果 ，那么 与 所成的角和 与 所成的角相等. 其中正确的命题有 ． (填写所有正确命题的编号） （15）有三张卡片，分别写有 1 和 2，1 和 3，2 和 3．甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后 说：“我与乙的卡片上相同的数字不是 2”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是 1”，  0,1 2n 1x 2x nx 1y 2y ny  1 1,x y  2 2,x y  ,n nx y m  4n m 2n m 4m n 2m n 1 2,F F 2 2 2 2: 1x yE a b  M E 1MF x 2 1 1sin 3MF F  E 2 3 2 3 ( )( )f x xR ( ) 2 ( )f x f x   1xy x  ( )y f x 1 1 2 2( , ),( , ), ,( , ),m mx y x y x y 1 ( ) m i i i x y    m 2m 4m ABC , ,A B C , ,a b c 4cos 5A  5cos 13C  1a  b  ,  ,m n , , / /m n m n     , / /m n  m n / / ,m   / /m  / / , / /m n   m  n  丙说：“我的卡片上的数字之和不是 5”，则甲的卡片上的数字是 ． （16）若直线 是曲线 的切线，也是曲线 的切线，则 ． 三.解答题：解答应写出文字说明，证明过程或演算步骤. 17.（本题满分 12 分） 为等差数列 的前 项和，且 记 ，其中 表示不超过 的最大整数，如 ． （Ⅰ）求 ； （Ⅱ）求数列 的前 1 000 项和． 18.（本题满分 12 分） 某险种的基本保费为 （单位：元），继续购买该险种的投保人称为续保人，续保人的本年度的保费与其上 年度的出险次数的关联如下： 上年度出险次数 0 1 2 3 4 5 保费 0.85 1.25 1.5 1.75 2 设该险种一续保人一年内出险次数与相应概率如下： 一年内出险次数 0 1 2 3 4 5 概率 0.30 0.15 0.20 0.20 0.10 0.05 （Ⅰ）求一续保人本年度的保费高于基本保费的概率； （Ⅱ）若一续保人本年度的保费高于基本保费，求其保费比基本保费高出 60%的概率； （Ⅲ）求续保人本年度的平均保费与基本保费的比值． 19.（本小题满分 12 分） 如图，菱形 的对角线 与 交于点 ， ，点 分别在 上， ， 交 于点 ．将 沿 折到 位置， ． （Ⅰ）证明： 平面 ； （Ⅱ）求二面角 的正弦值．[来源:Z#xx#k.Com] y kx b  ln 2y x  ln( 1)y x  b  nS  na n 1 7=1 28.a S ，  = lgn nb a  x x    0.9 =0 lg99 =1， 1 11 101b b b， ，  nb a  a a a a a a  ABCD AC BD O 5, 6AB AC  ,E F ,AD CD 5 4AE CF  EF BD H DEF EF D EF 10OD  D H  ABCD B D A C  [来源:学,科,网] 20.（本小题满分 12 分） 已知椭圆 的焦点在 轴上， 是 的左顶点，斜率为 的直线交 于 两点， 点 在 上， ． （Ⅰ）当 时，求 的面积； （Ⅱ）当 时，求 的取值范围． （21）（本小题满分 12 分） (Ⅰ)讨论函数 的单调性，并证明当 时， ； (Ⅱ)证明：当 时，函数 有最小值.设 的最小值为 ，求函数 的值域． 请考生在 22、23、24 题中任选一题作答,如果多做,则按所做的第一题计分,做答时请写清题号 （22）（本小题满分 10 分）选修 4-1：几何证明选讲 如图，在正方形 中， 分别在边 上（不与端点重合），且 ，过 点作 ，垂足为 ． (Ⅰ) 证明： 四点共圆； (Ⅱ)若 ， 为 的中点，求四边形 的面积． :E 2 2 13 x y t   x A E ( 0)k k  E ,A M N E MA NA 4,| | | |t AM AN  AMN 2 AM AN k xx 2f (x) x 2   e 0x  ( 2) 2 0xx e x    [0,1)a 2x = ( 0) xe ax ag xx   （ ） ( )g x ( )h a ( )h a ABCD ,E G ,DA DC DE DG D DF CE F , , ,B C G F 1AB  E DA BCGF （23）（本小题满分 10 分）选修 4—4：坐标系与参数方程 在直角坐标系 中，圆 的方程为 ． （Ⅰ）以坐标原点为极点， 轴正半轴为极轴建立极坐标系，求 的极坐标方程； （Ⅱ）直线 的参数方程是 （ 为参数）, 与 交于 两点， ，求 的斜率． （24）（本小题满分 10 分）选修 4—5：不等式选讲 已知函数 ， 为不等式 的解集． （Ⅰ）求 ； （Ⅱ）证明：当 时， ． xOy C 2 2( 6) 25x y   x C l cos sin x t y t      t l C ,A B | | 10AB  l 1 1( ) | | | |2 2f x x x    M ( ) 2f x  M ,a b M | | |1 |a b ab  