【数学】2020届一轮复习苏教版命题及其关系充分条件与必要条件学案
§1.3 命题及其关系、充分条件与必要条件
考情考向分析 命题的真假判断和充分、必要条件的判定是考查的主要形式,多与集合、函数、不等式、立体几何中的线面关系相交汇,考查学生的推理能力,题型为填空题,低档难度.
1.命题
用语言、符号或式子表达的,可以判断真假的陈述句叫做命题,其中判断为真的语句叫做真命题,判断为假的语句叫做假命题.
2.四种命题及其相互关系
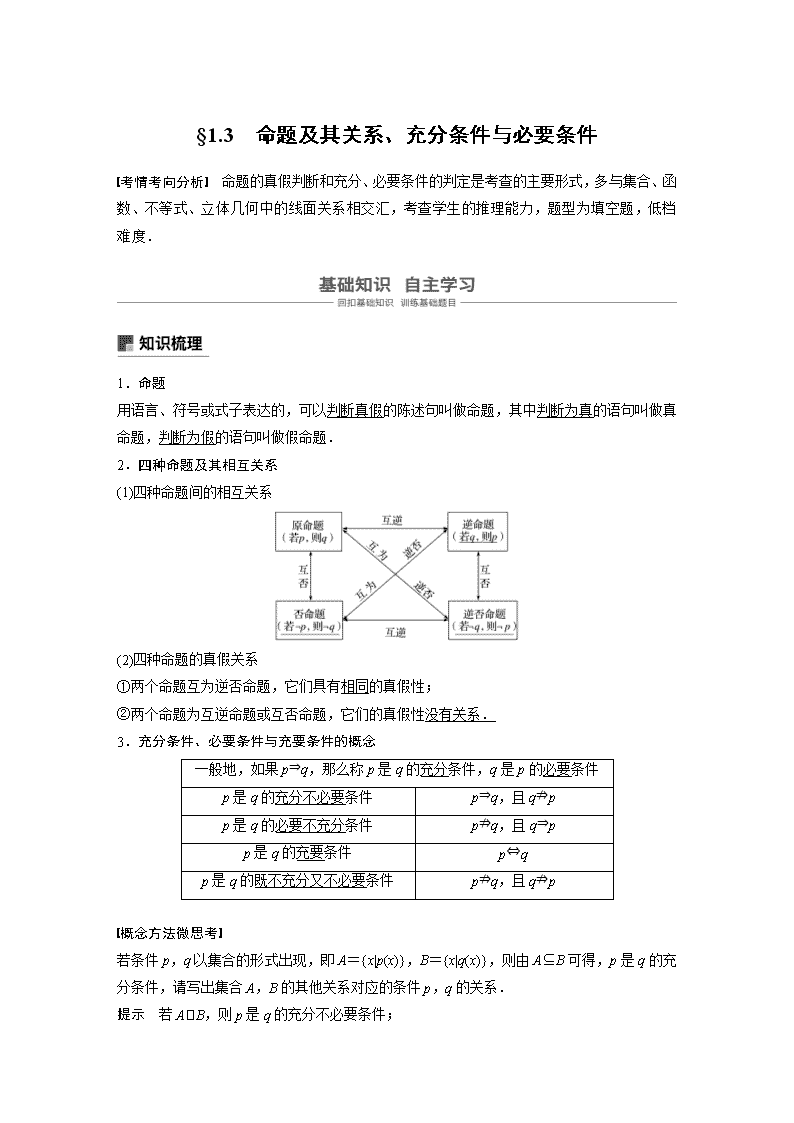
(1)四种命题间的相互关系
(2)四种命题的真假关系
①两个命题互为逆否命题,它们具有相同的真假性;
②两个命题为互逆命题或互否命题,它们的真假性没有关系.
3.充分条件、必要条件与充要条件的概念
一般地,如果p⇒q,那么称p是q的充分条件,q是p的必要条件
p是q的充分不必要条件
p⇒q,且q⇏p
p是q的必要不充分条件
p⇏q,且q⇒p
p是q的充要条件
p⇔q
p是q的既不充分又不必要条件
p⇏q,且q⇏p
概念方法微思考
若条件p,q以集合的形式出现,即A={x|p(x)},B={x|q(x)},则由A⊆B可得,p是q的充分条件,请写出集合A,B的其他关系对应的条件p,q的关系.
提示 若AB,则p是q的充分不必要条件;
若A⊇B,则p是q的必要条件;
若AB,则p是q的必要不充分条件;
若A=B,则p是q的充要条件;
若A⊈B且A⊉B,则p是q的既不充分又不必要条件.
题组一 思考辨析
1.判断下列结论是否正确(请在括号中打“√”或“×”)
(1)“对顶角相等”是命题.( √ )
(2)命题“若p,则q”的否命题是“若p,则綈q”.( × )
(3)当q是p的必要条件时,p是q的充分条件.( √ )
(4)若原命题为真,则这个命题的否命题、逆命题、逆否命题中至少有一个为真.( √ )
题组二 教材改编
2.[P8习题T2]下列命题是真命题的是________.(填序号)
①矩形的对角线相等;
②若a>b,c>d,则ac>bd;
③若整数a是素数,则a是奇数;
④命题“若x2>0,则x>1”的逆否命题.
答案 ①
3.[P7例1]“x-3=0”是“(x-3)(x-4)=0”的__________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充分不必要
题组三 易错自纠
4.命题“若x2>y2,则x>y”的逆否命题是____________.
答案 若x≤y,则x2≤y2
解析 根据原命题和其逆否命题的条件和结论的关系,得命题“若x2>y2,则x>y”的逆否命题是“若x≤y,则x2≤y2”.
5.“sin α>0”是“α是第一象限角”的____________条件.
答案 必要不充分
解析 由sin α>0,可得α是第一或第二象限角及终边在y轴正半轴上;若α是第一象限角,则sin α>0,所以“sin α>0”是“α是第一象限角”的必要不充分条件.
6.已知集合A=,B={x|-1
3,即m>2.
题型一 命题及其关系
1.下列命题是真命题的是________.(填序号)
①若=,则x=y;②若x2=1,则x=1;
③若x=y,则=;④若x2”是“<1”的________条件.(填“充分不必要”“必要不充分”“充要”或“既不充分又不必要”)
答案 充分不必要
解析 解不等式2x>2,得x>1;
不等式<1,即为>0,解得x>1或x<0.
∵{x|x>1}⊆{x|x>1或x<0},
∴“2x>2”是“<1”的充分不必要条件.
(2)已知条件p:x>1或x<-3,条件q:5x-6>x2,则綈p是綈q的____________条件.
答案 充分不必要
解析 由5x-6>x2,得20);q:>0.若p是q的充分不必要条件,则实数m的取值范围为__________.
答案 (0,2]
解析 由|2x+1|0),得-m<2x+10,得x<或x>1.
∵p是q的充分不必要条件,又m>0,
∴≤,∴0a+1或x-3,则a>-6”以及它的逆命题、否命题、逆否命题中假命题的个数为
________.
答案 2
解析 原命题正确,从而其逆否命题也正确;其逆命题为“若a>-6,则a>-3”是假命题,从而其否命题也是假命题.因此4个命题中有2个假命题.
2.命题“若a>b,则a+c>b+c”的否命题是________________.
答案 若a≤b,则a+c≤b+c
解析 否命题是将原命题的条件和结论都否定,故命题“若a>b,则a+c>b+c”的否命题是“若a≤b,则a+c≤b+c”.
3.“φ=”是“函数y=sin(x+φ)的图象关于y轴对称”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充分不必要
解析 若函数y=sin(x+φ)的图象关于y轴对称,则φ=+kπ,k∈Z,∴必要性不成立.
若φ=,则函数y=sin(x+φ)=cos x的图象关于y轴对称,∴充分性成立.
∴“φ=”是“函数y=sin(x+φ)的图象关于y轴对称”的充分不必要条件.
4.“若a≤b,则ac2≤bc2”,则原命题及命题的逆命题、否命题和逆否命题中真命题的个数是________.
答案 2
解析 其中原命题和逆否命题为真命题,逆命题和否命题为假命题.
5.有下列命题:
①“若x+y>0,则x>0且y>0”的否命题;
②“矩形的对角线相等”的否命题;
③“若m>1,则mx2-2(m+1)x+m+3>0的解集是R”的逆命题;
④“若a+7是无理数,则a是无理数”的逆否命题.
其中正确的是________.(填序号)
答案 ①③④
解析 ①的逆命题“若x>0且y>0,则x+y>0”为真,故否命题为真;
②的否命题为“不是矩形的图形对角线不相等”,为假命题;
③的逆命题为“若mx2-2(m+1)x+m+3>0的解集为R,则m>1”.
因为当m=0时,解集不是R,
所以应有即m>1.所以③是真命题;
④原命题为真,逆否命题也为真.
所以正确的命题序号是①③④.
6.直线l1:(3+m)x+4y=5-3m,l2:2x+(5+m)y=8.则“m≠-7”是“l1与l2相交”的________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 必要不充分
解析 因为l1与l2相交,所以(3+m)(5+m)≠8,
所以m≠-1且m≠-7.
所以“m≠-7”是“l1与l2相交”的必要不充分条件.
7.设p:实数x,y满足x>1且y>1,q:实数x,y满足x+y>2,则p是q的________条件.(选填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充分不必要
解析 当x>1,y>1时,x+y>2一定成立,即p⇒q,
当x+y>2时,可令x=-1,y=4,即q⇏p,
故p是q的充分不必要条件.
8.已知命题p:a≤x≤a+1,命题q:x2-4x<0,若p是q的充分不必要条件,则a的取值范围是________.
答案 (0,3)
解析 令M={x|a≤x≤a+1},
N={x|x2-4x<0}={x|00,则方程x2+x-m=0有实根”的逆命题为真命题;
④命题“若m2+n2=0,则m=0且n=0”的否命题是“若m2+n2≠0,则m≠0或n≠0”.
答案 ③
解析 命题③的逆命题为“若方程x2+x-m=0有实根,则m>0”.若方程有实根,则Δ=1+4m≥0,
即m≥-,不能推出m>0,所以不是真命题.
10.若“数列an=n2-2λn(n∈N*)是递增数列”为假命题,则λ的取值范围是________________.
答案
解析 若数列an=n2-2λn(n∈N*)为递增数列,则有an+1-an>0,即2n+1>2λ对任意的n∈N*
都成立,于是可得3>2λ,即λ<.
因为原命题为假命题,故所求λ的取值范围是.
11.在△ABC中,角A,B均为锐角,则“cos A>sin B”是“△ABC为钝角三角形”的____________条件.(填“充分不必要”“必要不充分”“充要”“既不充分又不必要”)
答案 充要
解析 因为cos A>sin B,所以cos A>cos,
因为角A,B均为锐角,所以-B为锐角,
又因为余弦函数y=cos x在(0,π)上单调递减,
所以A<-B,所以A+B<,
因为在△ABC中,A+B+C=π,所以C>,
所以△ABC为钝角三角形;
若△ABC为钝角三角形,角A,B均为锐角,
则C>,所以A+B<,所以A<-B,
所以cos A>cos,即cos A>sin B.
故“cos A>sin B”是“△ABC为钝角三角形”的充要条件.
12.已知不等式|x-m|<1成立的充分不必要条件是2且y>3”是“x+y>5”的充分条件;
②“b2-4ac<0”是“一元二次不等式ax2+bx+c<0的解集为R”的充要条件;
③“a=2”是“直线ax+2y=0平行于直线x+y=1”的充分不必要条件;
④“xy=1”是“lg x+lg y=0”的必要不充分条件.
其中真命题的序号为________.
答案 ①④
解析 ①当x>2且y>3时,x+y>5成立,反之不一定,所以“x>2且y>3”是“x+y>5”的充分不必要条件,故①为真命题;
②不等式的解集为R的充要条件是a<0且b2-4ac<0,故②为假命题;
③当a=2时,两直线平行,反之,若两直线平行,则=,所以a=2,所以“a=2”是“两直线平行”的充要条件,故③为假命题;
④lg x+lg y=lg(xy)=0,所以xy=1且x>0,y>0,所以xy=1必成立,反之不然,所以“xy=1”是“lg x+lg y=0”的必要不充分条件,故④为真命题.
综上可知,真命题是①④.
15.已知p:实数m满足3a0),q:方程+=1表示焦点在y轴上的椭圆,若p是q的充分条件,则a的取值范围是________________.
答案
解析 由2-m>m-1>0,解得1
查看更多