广东省汕头市 2016-2017 学年高二数学 3 月月考试题 文

广东省汕头市 2016-2017 学年高二数学 3 月月考试题 文

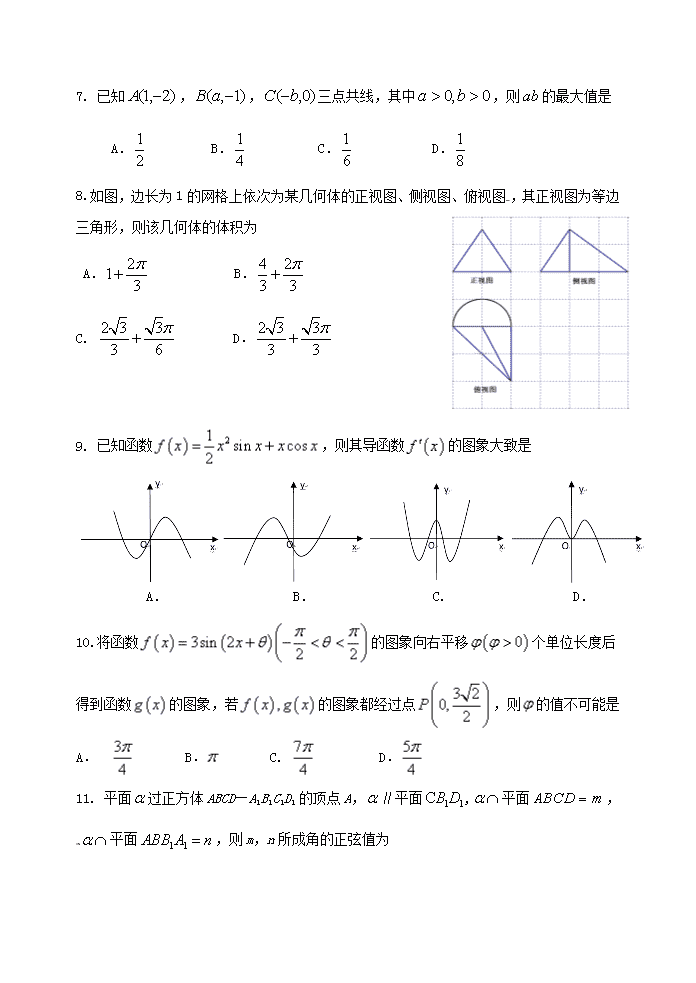
广东省汕头市 2016-2017 学年高二数学 3 月月考试题 文 一、选择题：本大题共 12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中，只 有一项是符合题目要 求的. 1.已知集合     | lg 3 , | 5A x y x B x x     ，则 A B  A． R B．  | 5x x  C． | 3x x  D． |3 5x x  2. 命题：“∀x＞0，x2+x≥0”的否定形式是 A．∀x≤0，x2+x＞0 B．∀x＞0，x2+x≤0 C．  x0＞0，x0 2+x0＜0 D．  x0≤0，x0 2+x0＞0 3. “ 1- 4a  ”是“关于 x 的不等式 2 1 0ax x   恒成立”的 A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 4.双曲线   2 2 2 2 14 x y m Zm m    的离心率为 A．3 B．2 C. 5 D． 3 5. 变量满足约束条件,则目标函数的最小值为 A.2 B.4 C.5 D.6 6.下表是降耗技术改造后生产甲产品过程中记录的产量 x（吨）与相应的生产能耗 y （吨 标准煤）的几组对应数据，根据表中提供的数据，求出 y 关于 x 的线性回归方程为 ˆ 0.7 0.35y x  ，则表中 m 的值为 x 3 4 5 6 y 2.5 m 4 4.5 A．4 B． 3 C. 3 .5 D．3.15 7. 已知 )2,1( A ， )1,( aB ， )0,( bC  三点共线，其中 0,0  ba ，则 ab 的最大值是 A． 2 1 B． 4 1 C． 6 1 D． 8 1 8.如图，边长为 1 的网格上依次为某几何体的正视图、侧视图、俯视图 ，其正视图为等边 三角形，则该几何体的体积为 A． 21 3  B． 4 2 3 3  C. 2 3 3 3 6  D． 2 3 3 3 3  9. 已知函数   21 sin cos2f x x x x x  ，则其导函数  f x 的图象大致是 A． B． C. D． 10.将函数    3sin 2 2 2f x x           的图象向右平移  0   个单位长度后 得到函数  g x 的图象，若    ,f x g x 的图象都经过点 3 20, 2P       ，则 的值不可能是 A． 3 4  B． C. 7 4  D． 5 4  11. 平面 过正方体 ABCD—A1B1C1D1 的顶点 A， ∥平面 1 1CB D ,  平面 ABCD m ，   平面 1 1ABB A n ，则 m，n 所成角的正弦值为 A． 3 2 B． 2 2 C. 3 3 D． 1 3 12.已知函数     3 2ln , 5af x x x g x x xx      ，若对任意的 1 2 1, ,22x x     ，都有    1 2 2f x g x  成立，则实数 a 的取值范围是 A．  1, B．  0, C.  ,0 D． , 1  二、填空题:本题共 4 小题,每小题 5 分，满分 20 分，将答案填在答题纸上 13.一个直六棱柱的底面是边长为 2 的正六边形，侧棱长为 3，则它的外接球的表面积 为 ． 14.在 ABC 中，内角为 A，B ，C，若sin sin cosA C B ，则 ABC 的形状一定是 15.若向量 ,a b  夹角为 3  ，且 2, 1a b   ，则 a 与 2a b  的夹角为 16.已知实数 ,a b 满足  ln 1 3 0b a b    ，实数 ,c d 满足 2 5 0d c   ，则    2 2a c b d   的最小值为 三、解答题 ：解答应写出文字说明、证明过程或演算步骤. 17. 已知公差不为 0 的等差数列 na 的前 n 项和为 nS ，且 3 1 3 79, , ,S a a a 成等比数列. （1）求数列 na 的通项公式； （2）数列 nb 满足  1 2n n nb a  ，求数列 nb 的前 n 项和 nT . 18. 某中学一位 高三班主任对本班 50 名学生学习积极性和对待班级工作的态度进行调 查，得到的统计数据如下表所示： 积极参加班级工作 不积极参加班级工作 合计 学习积极性高 18 7 25 学习积极性不高 6 19 25 合计 24 26 50 （1）若不积极参加班级工作且学习积极性高的 7 名学生中有两名男生，现从中抽取两名 学生参加某项活动，问两名学生中有 1 名男生的概率是多少？ （2）有多少的把握认为“学生的学习积极性与对待班级工作的态度”有关系？请说明理 由. 附：  2 0P K k 0.10 0.05 0.025 0.010 0.005 0.001 0k 2.706 3.841 5.024 6.635 7.879 10.828        2 2 n ad bcK a b c d a c b d      19. 如 图 ， 四 边 形 ABCD 是 菱 形 ， PD  平 面 ABCD ， // , 2 2, 60PD BE AD PD BE DAB      ,点 F 为 PA 的中点. （1）求证： EF  平面 PAD ； （2）求点 P 到平面 ADE 的距离. 2 0.已知抛物线  2 1 : 2 0C y px p  的焦点为 F ，抛物线上存在一点G 到焦点的距离为 3，且点G 在圆 2 2: 9C x y  上. （1）求抛物线 1C 的方程； （2）已知椭圆   2 2 2 2 2: 1 0x yC m nm n     的一个焦 点与抛物线 1C 的焦点重合，且离心率为 1 2 。直线 : 4l y kx  交椭圆 2C 于 ,A B 两个不同 的点，若原点 O 在以线段 AB 为直径的圆的外部，求实数 k 的取值范围． 21. 设函数 f(x)＝ax2ln x＋b(x－1)(x＞0)，曲线 y＝f(x)过点(e，e2－e＋1)，且在点(1,0) 处的切线方程为 y＝0. (1)求 a，b 的值； (2)证明：当 x≥1 时，f(x)≥(x－1)2； (3)若当 x≥1 时，f(x)≥m(x－ 1)2 恒成立，求实数 m 的取值范围． 文数月考试 卷答案 一、选择题 1-5: ACBBB 6-10:BDCCD 11、12：AA 二、填空题 13. 25 14.直角三角形 15. 6  16. 1 三、解答题 17.解：（1）由题得， 2 3 1 7a a a ，设等差数列 na 的公差为 d ，则   2 1 1 12 6a d a a d   ， 化简，得 1 1 2d a 或 0d  （舍）. 当 1 1 2d a 时， 1 1 1 1 2 3 1 93 92 2 2S a a a     ，得 1 2,d 1a   ， ∴    1 1 2 1 1na a n d n n        ， 即  1 *na n n N   ； （2）由题意可知， 2n nb n  ， ∴ 2 1 2 1 2 2 2 2n n nT b b b n           ，①  2 3 12 1 2 2 2 1 2 2n n nT n n           ，② ①-②，得  2 3 1 12 2 2 2 2 1 2 2n n n nT n n              ， ∴   11 2 2n nT n    . 18.解： （1）设这 7 名学生分别为 , , , , ,A,Ba b c d e （大写为男生），则从中抽取两名学生 的情况有：           , , , , , , , , , , ,d e d A d B e A e B A B ， 共 21 种情况，其中有 1 名男生的有 10 种情况，∴ 10 21P  ．                               , , , , , , , , , , , , , , , , , , , , , , , , , , , , , a b a c a d a e a A a B b c b d b e b A B b c d c e c A c B （2）由题意得，  2 2 50 18 19 6 7 11.538 10.82824 26 25 25K         ，故有 99.9%的把握认为 “学生的学习积极性与对待班级工作的态度”有关系． 19. 20.解：（1）设点G 的坐标为 0 0,x y ． 由题可知， 0 2 2 0 0 2 0 0 32 9 2 px x y y px          ，解得 0 01, 2 2, 4x y p    ， ∴抛物线 1C 的方程为 2 8y x ； （2）由（1）得，抛物线 1C 的焦点  2,0F ， ∵椭圆 2C 的一个焦点与抛物线 1C 的焦点重合， ∴椭圆 2C 的半焦距 2c  ， 即 2 2 2 4m n c   ，又椭圆 2C 的离心率为 1 2 ， ∴ 2 1 2m  ，即 4, 2 3m n  ， ∴椭圆 2C 的方程为 2 2 116 12 x y  ， 设    1 1 2 2, , ,A x y B x y ， 由 2 2 4 116 12 y kx x y     ，得 2 24 3 32 16 0k x kx    ， 由韦达定理，得 1 2 1 22 2 32 16,4 3 4 3 kx x x xk k     ， 由 0  ，得   2 232 4 16 4 3 0k k     ， 解得 1 2k  或 1 2k   ，① ∵原点 O 在以线段 AB 的圆的外部，则 0OA OB    ， ∴             1 1 2 2 1 2 1 2 1 2 1 2 2 1 2 1 2 , , 4 4 1 4 16 OA OB x y x y y y x x kx kx x x k x x k x x                     2 2 2 2 2 16 4 316 321 4 16 04 3 4 3 4 3 kkk kk k k            ， 即 2 3 2 3 3 3k   ，② 由①，② 得，实数 k 的范围是 2 3 1 3 2k    或 1 2 3 2 3k  ，即实数 k 的取值范围是 2 3 1 1 2 3, ,3 2 2 3                ． 21. (1)函数 f(x)＝ax2ln x＋b(x－1)(x＞0)，可得 f′(x)＝2aln x＋ax＋b， 因为 f′(1)＝a＋b＝0，f(e)＝ae2＋b(e－1)＝a(e2－e＋1)＝e2 －e＋1， 所以 a＝1，b＝－1. 2 分 (2)证明：f(x)＝x2ln x－x＋1， 设 g(x)＝x2ln x＋x－x2(x≥1)， g′(x)＝2xln x－x＋1，(g′(x))′＝2ln x＋1＞0， 所以 g′(x)在[0，＋∞)上单调递增， 所以 g′(x)≥g′(1)＝0， 所以 g(x)在[0，＋∞)上单调递增， 所以 g(x)≥g(1)＝0，所以 f(x)≥(x－1)2. 6 分 (3)设 h(x)＝x2ln x－x－m(x－1)2＋1， h′(x)＝2xln x＋x－2m(x－1)－1， 由(2)中知 x2ln x≥(x－1)2＋x－1＝x(x－1)， 所以 xln x≥x－1，所以 h′(x)≥3(x－1)－2m(x－1)， ①当 3－2m≥0 即 m≤3 2 时，h′(x)≥0， 所以 h(x)在[1，＋∞)单调递增， 所以 h(x)≥h(1)＝0，成立． ②当 3－m＜0 即 m＞3 2 时， h′(x)＝2xln x－(1－2m)(x－1)， (h′(x))′＝2ln x＋3－2m， 令(h′(x))′＝0，得 x0＝e2m－3 2 ＞1， 当 x∈[1，x0)时，h′(x)＜h′(1)＝0， 所以 h(x)在[1，x0)上单调递减，所 以 h(x)＜h(1)＝0，不成立． 综上，m≤3 2 . 12 分